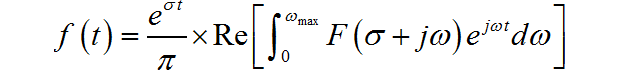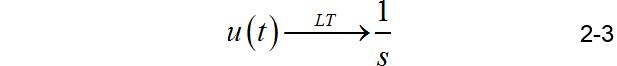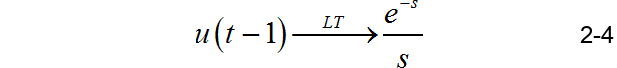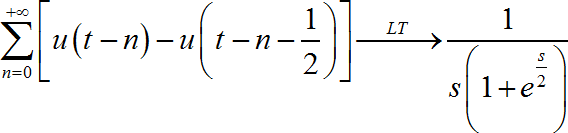Laplace数值逆运算的讨论

■ 问题提出

---

在博文 逆Laplace数值逆变换 给出了数值计算Laplace逆变换的简易程序。其中存在以下几个问题需要讨论：

• 问题1： 程序实现过程原理以及优化；
• 问题2： 运算参数：$\sigma$，${\omega }_{\max }$，$N_{\mathrm{int}}$对于积分数值的影响。从上篇博文中明显看到有些计算出的结果大大偏离的实际值。比如其中的函数$\sin \left(t\right)$所计算出来的幅值超过了1.

 

01程序实现原理以及优化

---

1.Laplace逆运算

所以，算法的核心是对$F\left(s\right)$进行傅里叶反变换，然后在乘以$e^{\sigma t}$。

由于确认变换后的函数$f\left(t\right)$是实函数，因此，为了节省计算时间，只对傅里叶反变换的积分，进行正半轴的积分，同时积分的上限有参数${\omega }_{\max }$决定。对积分的数值取齐实部，再乘以2便可以得到$f\left(t\right)$。

2.Python积分程序实现优化

使用梯形积分来实现函数的积分，可以获得更精确的积分值。理论分析可知：

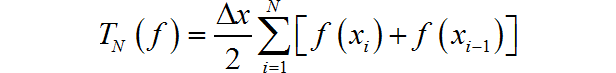
其中$\Delta x=\left(b-a\right)/N$ 以及 $x_i=a+i\Delta x$。那么积分误差上限为：

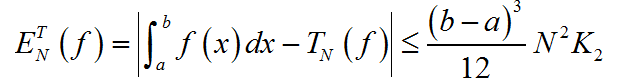
其中，$\left|f^{{}^{\prime \prime }}\left(x\right)\right|\le K_2$， $x\in \left[a,b\right]$。

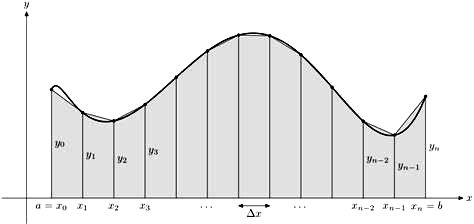
^{▲ 图2.1 梯形积分方法示意图}

计算$T_N\left(f\right)$可以由两种方式：

方式1： 对左、右黎曼积分加权平均：

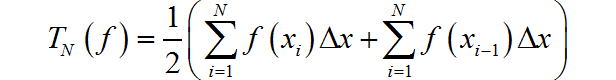
方式2： 利用如下的公式计算：

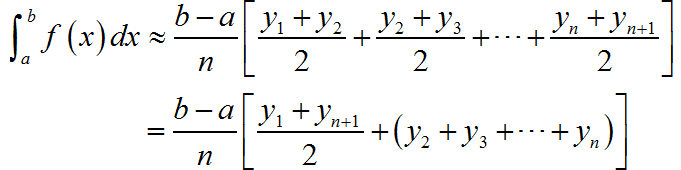
最后实现的代码为：

def trapz(f, a, b, N=50):
    x = linspace(a, b, N+1)
    y = f(x)
    y_right = y[1:]
    y_left = y[:-1]
    dx = (b-a) / N
    T = dx/2 * sum(y_right + y_left)
    return T

利用上述公式，对$\sin \left(t\right)$进行积分测试：

printf(trapz(sin, 0, pi/2, 1000))

所得到结果为：0.9999997943832332。
可以看到使用n=1000对应的结果后面的积分精度达到了小数点后面6位9的小数点的位数。

3.实现Laplace逆运算

通过上面梯形积分方法，实现Laplace数值逆变换，具体的子程序如下面所示。

#------------------------------------------------------------
def invlt(t, fs, sigma, omiga, nint):
    omigadim = linspace(0, omiga, nint+1, endpoint=True)
    y = [(exp(1j*o*t) * fs(sigma+1j*o)).real for o in omigadim]
    y_left = y[:-1]
    y_right = y[0:]
    T = sum(y_right + y_left) * omiga/nint
    return exp(sigma*t) * T/ pi / 2

#------------------------------------------------------------
def fs(s):
    return 1/(s*s+1)

#------------------------------------------------------------
sigma = 0.2
omiga=200
nint=omiga*50

tdim = linspace(0, 2*pi* 3, 200)
ft = [invlt(t, fs, sigma, omiga, nint) for t in tdim]

 

02一些基本函数的实验

---

下面通过对一些基本常见函数的laplace变换，来测试一下上述程序的性能。

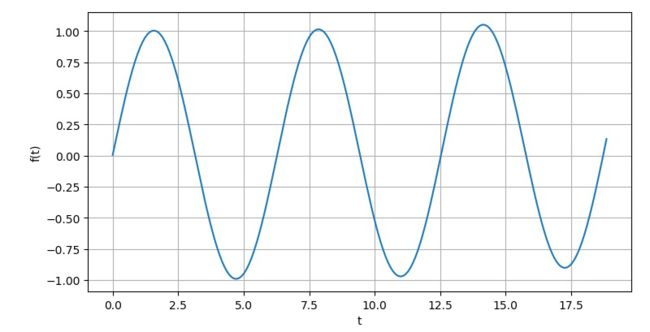
Ⅰ.sin(t)

sigma=0.2, omiga=200, nint=omiga*50

Ⅱ.exp(-t)

sigam=-1+0.1, omiga=200, nint=omiga*50

Ⅲ.u(t)

Ⅳ.u(t-1)

Ⅴ.周期化脉冲信号

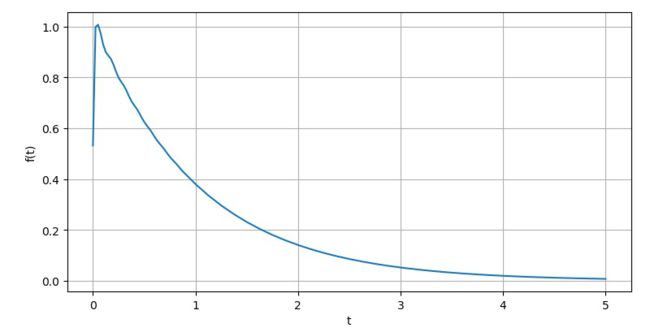
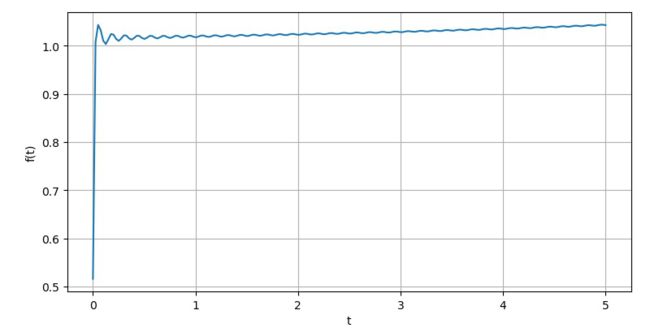
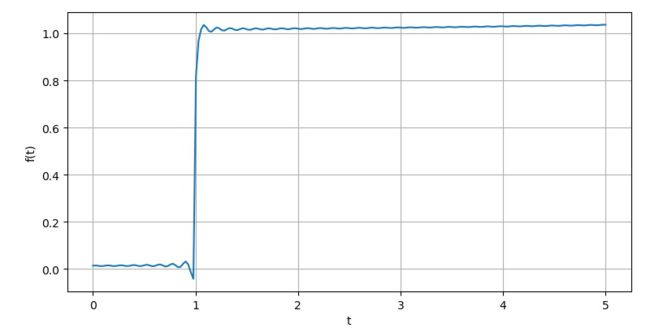
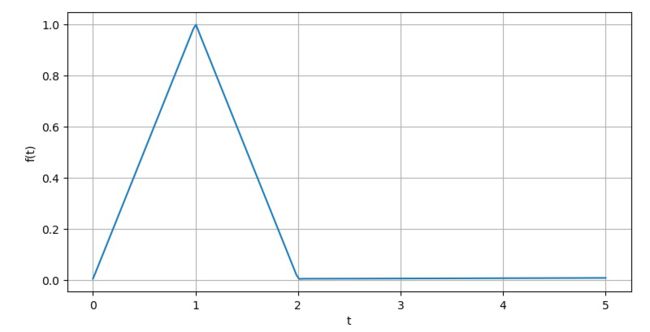
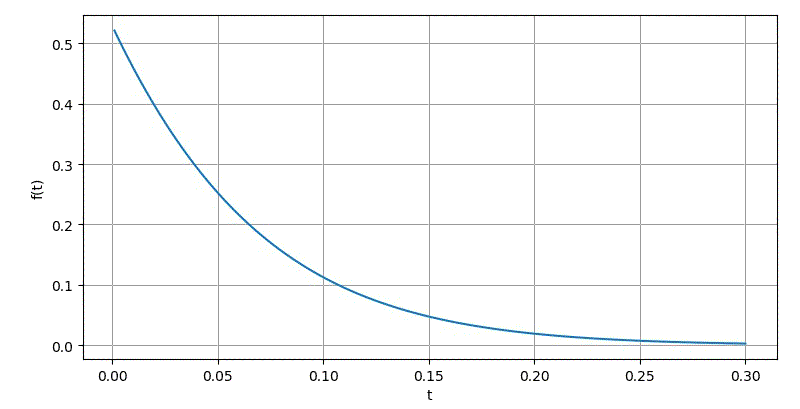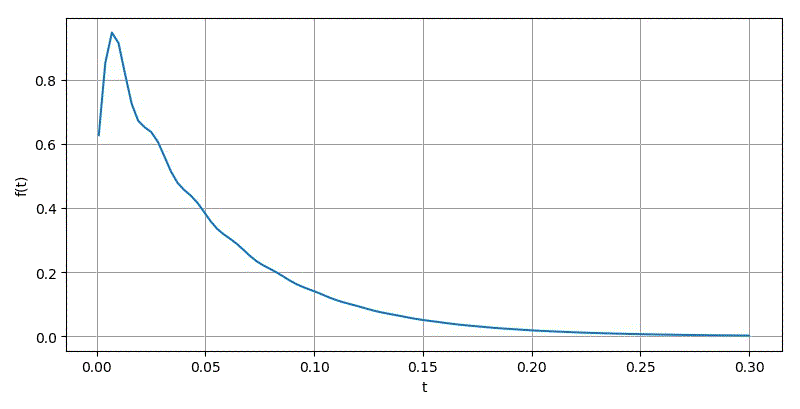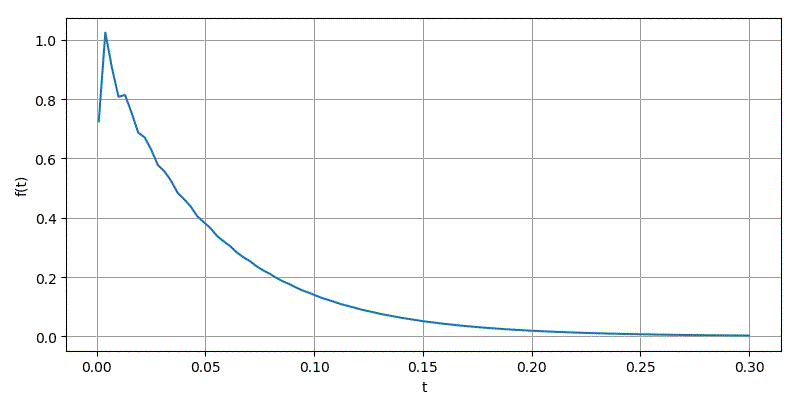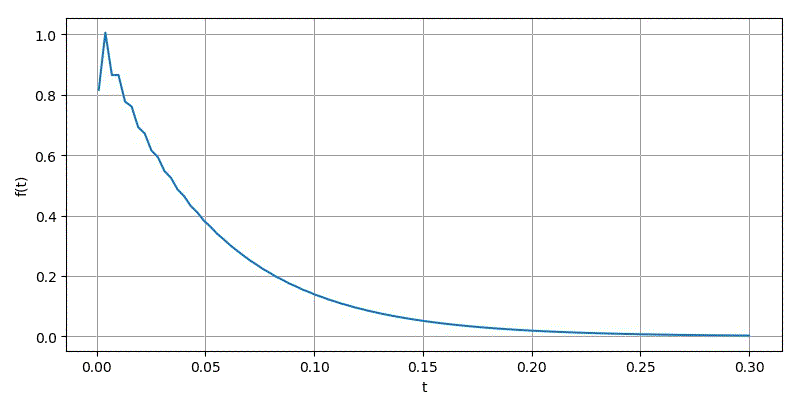
Ⅵ.三角形

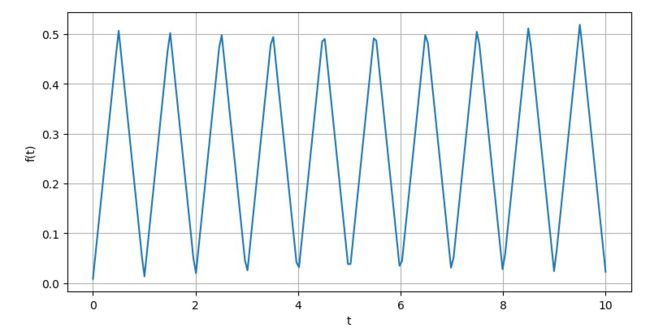
^{▲ omiga从10变化到1000}

 

※ 结论

---

通过原理分析，可以获得建议的Laplace数值逆运算的正确的PYTHON算法程序。

这个程序是直接对Laplace反变换公式利用梯形积分方法获得计算结果。通过对几种常见的信号Laplace的反变换，验证了这个算法的正确性。

通过在此过程，可以看到，对于参数sigma, omiga, nint对于计算结果还是有很大的影响。另外，对于时间t，只能在比较小的范围内有效，当t超过一定长度，前面所计算的结果都会出现比较大的误差。

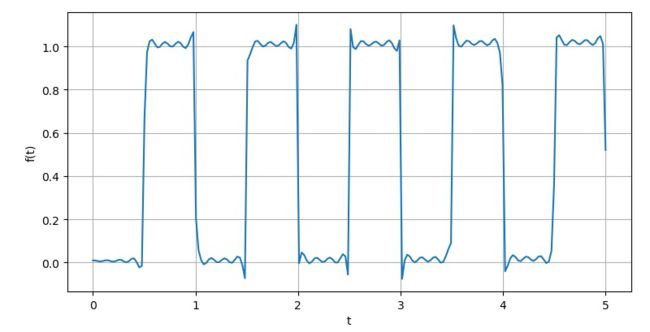
^{▲ 对于方波进行Laplace数值反变换的结果}

 

§ 参考文献

---

1. Numerical Inverse Laplace Transorms for Electrical Engineering Simulation

2. Laplace transform numerical inversion

3. MATLAB Algorithms for the laplace Transform inversion