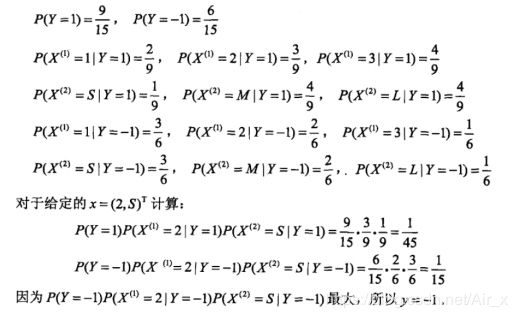贝叶斯决策、朴素贝叶斯算法与词频统计

贝叶斯决策

概率公式

• 事件A发生的可能性：记为$P(A)$
• 事件A和事件B同时发生的概率：记为$P(AB)$
• 条件概率：设$A，B$为任意两个事件，若$P(A)>0$，我们称在已知事件A发生的条件下，事件B发生的概率为条件概率，记为$P(B|A)$，$$P(B|A)=\frac{P(AB)}{P(A)}$$
• 全概率公式：
  如果${\bigcup }_{i=1}^n{A}_i=\Omega ,A_i{A}_j=\varphi (\text{ 对一切 }i\ne j),\mathrm{P}\left({\mathrm{A}}_i\right)>0$，则对于任一事件$B$，有$$P(B)=\sum _{i=1}^{n}P(A_i)P(B|A_i)$$
  
  从图上看就是，$B$发生的概率等于$B$与$A_i$同时发生的概率相加
• 贝叶斯公式(逆概率公式)
  如果${\bigcup }_{i=1}^n{A}_i=\Omega ,A_i{A}_j=\varphi (\text{ 对一切 }i\ne j),\mathrm{P}\left({\mathrm{A}}_i\right)>0$，则对于任一事件$B$，只要$P(B)>0$，有$$P\left(A_j|B\right)=\frac{P\left(A_{j}B\right)}{P(B)}=\frac{P\left(A_j\right)P\left(B|A_j\right)}{{\sum }_{i=1}^{n}P\left(A_i\right)P\left(B|A_i\right)}(i,j=1,2,\dots ,n)$$

基于风险最小化的贝叶斯准则

假设有$N$个类别：$y=\{c_1,c_2,\dots ,c_n\}$，基于后验概率$P(c_i|x)$将样本$x$分到 $c_i$的风险（也称期望损失）为：
$$R(c_i|x)=\sum _{j=1}^{N}los{s}_{ij}P(c_j|x)$$，其中$los{s}_{ij}$为将样本分类错误产生的损失。

• 贝叶斯判定准则：要使总体风险最小化，则只需要每个样本的条件风险$R(c_i|x)$最小化。即：
  $$h^{\ast }(\mathbf{x})=\underset{c\in \mathcal{Y}}{\mathrm{argmin}}R(c|\mathbf{x})$$
  $h^{\ast }$称为贝叶斯最优分类器，总体风险：$R(h^{\ast })=E_x[R(h^{\ast }(x)|x)]$称为贝叶斯风险，$1-R(h^{\ast })$反映分类器达到的最佳精度

基于错误率最小化的贝叶斯准则

对于最小化分类错误率，将分类错误损失记为$$los{s}_{ij}=\{\begin{array}{ll}0,& i=j\\ 1,& i\ne j\end{array}$$

• 条件风险变为：$R(c|x)=1-P(c|x)$
• 最优分类器准则为：$h^{\ast }(\mathbf{x})=\underset{c\in \mathcal{Y}}{\mathrm{argmin}}P(c|\mathbf{x})$，即将样本$x$分为后验概率$P(c|x)$最大的类别标记。

两种模型

• 判别模型：给定样本$x$通过直接建模$P(c|x)$来预测$c_i$。决策树、BP神经网络、支持向量机、线性回归、逻辑回归等属于判别模型
• 生成模型：对联合概率分布$P(x,c)$建模，再由此获得$P(c|x)$。朴素贝叶斯、高斯混合模型、隐马尔科夫模型等属于生成模型。
• 关系：由生成模型可以得到判别模型，但由判别模型得不到生成模型。

朴素贝叶斯算法

• 朴素贝叶斯算法属于生成模型，对于生成模型考虑：$P(c|x)=\frac{P(x,c)}{P(x)}$，用于文本分类中

使用条件概率公式：$P(c|x)=\frac{P(c)P(x|c)}{P(x)}$，$P(c)$为每个类别的概率，是先验概率，$P(x|c)$为样本在类别$c$中发生的条件概率。

• 先验概率$P(c)$，根据大数定律，可通过各类样本出现的频率来进行估计
• 条件概率$P(x|c)=\frac{P(xc)}{P(c)}$。不过对于较大的数据集中，直接使用频率估计$P(x|c)$不可行。因此，可使用极大似然估计法进行估计，先前已介绍过极大似然估计，这里就不介绍了。

朴素贝叶斯分类器

为解决$P(c|x)$难以估计的问题，朴素贝叶斯是基于贝叶斯定理与特征条件独立假设的分类方法。因此，$$P(c|\mathbf{x})=\frac{P(c)P(\mathbf{x}|c)}{P(\mathbf{x})}=\frac{P(c)}{P(\mathbf{x})}\prod _{i=1}^{n}P\left(x_i|c\right)$$

对于所有类别来说，$P(x)$是相同的，所以朴素贝叶斯分类器为：
$$h_{nb}(\mathbf{x})=\underset{c\in \mathcal{Y}}{\mathrm{argmax}}P(c)\prod _{i=1}^{d}P\left(x_i|c\right)$$

小例子

假设有一训练集集包含100个人，包含身体颜色特征和头发形状特征，其中有60个非洲人（黑卷*47, 黑直*1, 黄卷*11, 黄直*1），有40个亚洲人（黑卷*1, 黄卷*4, 黄直*35）

1. 计算先验概率：$P(非洲)=\frac{60}{100}，P(亚洲)=\frac{40}{100}$
2. 计算每个特征的条件概率：
   
3. 预测样本 (黑，卷，地区未知) 属于哪个地区，根据朴素贝叶斯算法：$$\begin{gathered} P(非洲|黑卷)=P(非洲)P(黑|非洲)P(卷|非洲)=\frac{60\ast 48\ast 58}{100\ast 60\ast 60} \\ P(亚洲|黑卷)=P(亚洲)P(黑|亚洲)P(卷|亚洲)=\frac{40\ast 1\ast 5}{100\ast 40\ast 40} \end{gathered}$$
   因此，这个样本预测为非洲地区的

拉普拉斯平滑

若数据集中出现某个属性值在训练集中没有与某个类同时出现过，
假设$P(卷|非洲)=0$， $P(卷|亚洲)=0.001$，则样本(黑，卷，地区未知) 会被预测为亚洲地区：$$\begin{gathered} P(非洲|黑卷)=P(非洲)P(黑|非洲)P(卷|非洲)=0 \\ P(亚洲|黑卷)=P(亚洲)P(黑|亚洲)P(卷|亚洲)=0.00001 \end{gathered}$$由于P(卷|非洲)概率为0，导致无论样本其他属性如何，都会被预测为亚洲地区，这显然不合理。

• 为避免这种情况发生，使用了平滑操作

1. 改造先验概率公式：
   $P(非洲)=\frac{60+\lambda }{100+len[亚洲,非洲]\cdot \lambda }=\frac{60+\lambda }{100+2\lambda }$
   $----------$
   一般形式：$P(c_i)=\frac{D_{c_i}+\lambda }{D+N\ast \lambda }$，$c_i$为某个类别，$D_{c_i}$为该类别的样本数，$D$为训练集个数，$N$为训练集中可能的类别数
   $----------$
2. 改造每个特征的条件概率公式：
   $P(黑|非洲)=\frac{48+\lambda }{60+len[黑,白]\cdot \lambda }=\frac{48+\lambda }{60+2\lambda }$
   $P(直|非洲)=\frac{2+\lambda }{60+len[直,卷]\cdot \lambda }=\frac{2+\lambda }{60+2\lambda }$
   $----------$
   一般形式：$P(x_i|c_i)=\frac{D_{c_i{x}_i}+\lambda }{D_{c_i}+N_i\ast \lambda }$，$c_i$为某个类别，$x_i$为该类别下的某个特征(属性)，$D_{c_i}$为该类别$c_i$的样本数，$D_{c_i{x}_i}$为类别$c_i$的特征$x_i$的个数，$N_i$为类别$c_i$中可能的特征数
   $----------$

• $\lambda >0$，当$\lambda =1$时，称为拉普拉斯平滑

例子

不进行平滑操作

进行拉普拉斯平滑操作

python实现

# python3.7
# -*- coding: utf-8 -*-
#@Author    : huinono
#@Software  : PyCharm

import warnings
import numpy as np
import pandas as pd
import matplotlib as mpl
import matplotlib.pyplot as plt

warnings.filterwarnings('ignore')

mpl.rcParams['font.sans-serif'] = 'SimHei'
mpl.rcParams['axes.unicode_minus'] = 'False'

plt.rcParams['font.sans-serif'] = 'SimHei'
plt.rcParams['axes.unicode_minus'] = 'False'

class bayes_principle(object):
    def __init__(self):
        pass

    def tokey(self,col_name,category, y):
        # 定义写key的函数,比如产生字符 'X1=3|Y=1'
        return col_name + "=" + str(category) + "|Y=" + str(y)

    def run(self):
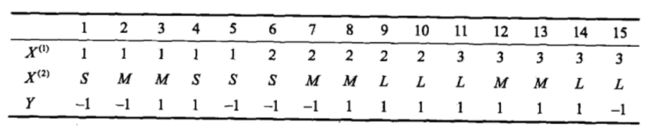
        df = pd.read_csv("../datas/bayes_lihang.txt")
        print(df.T)
        lam = 1  # 拉普拉斯  平滑因子
        P = {}  # 用于存储所有概率的字典
        Y = df["Y"].value_counts().keys()  # 获取类别种类的list   Y = [1, -1]
        col_names = df.columns.tolist()[:-1]  # 获取特征列名   x1,x2
        "使用拉普拉斯平滑处理，计算概率，并使用字典存储"
        for y in Y:  # 遍历每个类别
            df2 = df[df["Y"] == y]  #
            p = (df2.shape[0] + lam) / (df.shape[0] + len(Y) * lam)  # 计算先验概率
            P[y] = p  # 将先验概率加入P
            for col_name in col_names:  # 遍历每个特征
                categorys = df2[col_name].value_counts().keys()  # 获取每个特征下特征值种类的list
                for category in categorys:  # 遍历每个特征值
                    p = (df2[df2[col_name] == category].shape[0] + lam) / (
                        # 计算在某类别下，特征=某特征的条件概率
                            df2.shape[0] + len(categorys) * lam)
                    P[self.tokey(col_name, category, y)] = p  # 将条件概率加到P

        X = [2, "S"]
        res = []  # 用于存储属于某一类别的后验概率
        for y in Y:  # 遍历类别
            p = P[y]  # 获取先验概率
            for i in range(len(X)):  # 遍历特征
                p *= P[self.tokey(col_names[i], X[i], y)]  # 获取条件概率
            # print(p)
            res.append(p)  # 将后验概率加入res
        print(res)
        print(Y[np.argmax(res)])  # 返回最大的后验概率对应的类别

特征工程之词频统计

文本类数据处理的最重要的是需要将文本数据转换为数值型数据，一般情况是将文本转换为一个向量

TF(term frequency)与TF-IDF(term frequency–inverse document frequency)

• $TF=某词在文中出现次数$
• $IDF=\log \frac{1+n_d}{1+df(d,t)}+1$，$n_d$表示文章数量，$df$表示某词在该词文档中出现的频数
• $TF-IDF=TF\ast IDF$

为什么有TF-IDF：
在文章中，出现次数最多的词是----“的”、“是”、“在”、‘the’、‘a’、'is’等等----这一类最常用的词，这些词对文档的实际内容几乎没有任何有意义的信息。如果我们把这些数据直接输入分类器，那么这些非常频繁的词将掩盖一些重要词的频率和结果。
为了将计数特性重新加权为适合分类器使用的浮点值，通常使用TF-IDF转换。

例子

有文本[‘我爱你’ , ‘我恨你恨你’’]，计算"爱"字的TF与TF-IDF：
$TF=1$，$IDF=\log \frac{1+2}{1+1}+1=1.405$，$TF-IDF=1\times 1.405=1.405$

python实现

import numpy as np
import pandas as pd
from sklearn.feature_extraction.text import CountVectorizer,TfidfVectorizer
class WordFrequency(object):
    def __init__(self):
        pass
    def TF(self):
        X = ['我 爱 你', '我 恨 你 恨 你']
        # 正则化处理，有效字符为字母数字和汉字
        countCoder = CountVectorizer(token_pattern="[a-zA-Z|\u4e00-\u9fa5]+")
        X = countCoder.fit_transform(X)
        print(countCoder.get_feature_names())
        print(X.toarray())

    def TF_IDF(self):
        X = ['我 爱 你', '我 恨 你 恨 你']
        tiCoder = TfidfVectorizer(norm=None, token_pattern="[a-zA-Z|\u4e00-\u9fa5]+")
        X2 = tiCoder.fit_transform(X)
        print(tiCoder.get_feature_names())
        print(X2.toarray())

贝叶斯家族简介

多项式朴素贝叶斯

伯努利朴素贝叶斯

高斯朴素贝叶斯

python实现一些数据分类

# python3.7
# -*- coding: utf-8 -*-
#@Author    : huinono
#@Software  : PyCharm

import warnings
import numpy as np
import pandas as pd
import matplotlib as mpl
import matplotlib.pyplot as plt
from sklearn.pipeline import Pipeline
from sklearn.metrics import accuracy_score
from sklearn.neighbors import KNeighborsClassifier
from sklearn.model_selection import train_test_split
from sklearn.naive_bayes import MultinomialNB,GaussianNB
from sklearn.feature_extraction.text import CountVectorizer,TfidfVectorizer
from sklearn.preprocessing import StandardScaler

class NBayes_sklearn(object):
    def __init__(self):
        pass
    def text_classifier(self):
        df = pd.read_csv("../datas/bayes_xinxi.txt")  # 读取数据
        # 正则匹配，a-z，A-Z,所有中文
        tfCoder = CountVectorizer(token_pattern="[a-zA-Z|\u4e00-\u9fa5]+")  # TF模型
        X = df["words"]
        Y = df["Y"]
        X = tfCoder.fit_transform(X)  # 训练TF模型
        print(tfCoder.get_feature_names())
        print(X.toarray())
        X_ = ["Chinese Chinese Chinese Tokyo Japan"]  # 训练数据
        X_ = tfCoder.transform(X_).A  # A相当于toarray() 将训练数据转为array类型
        model = MultinomialNB()
        model.fit(X, Y)
        print(model.predict(X_))
        print('-----------')
        print(Y[model.predict(X_)])

    def gametext(self):
        df = pd.read_csv("../datas/bayes_wangzhe.txt", header=None)
        X = df[1]
        Y = df[0]
        tfCoder = TfidfVectorizer(token_pattern="[a-zA-Z|\u4e00-\u9fa5]+")
        X = tfCoder.fit_transform(X)
        print(tfCoder.get_feature_names())
        print(X.toarray())
        X_train, X_test, y_train, y_test = train_test_split(X, Y, test_size=0.2, random_state=42)
        model = MultinomialNB()
        model.fit(X_train, y_train)
        print(model.predict(X_train))
        print(y_train.values)
        a = ["残血 的 安琪拉 打 不 过 鲁班", "这 一波 大龙 别 再 被 抢 了",
             "你 在 石头 那 不要 动，我 去 买 几个 橘子"]
        # print(tfCoder.transform(a).todense())
        print(model.predict(tfCoder.transform(a)))

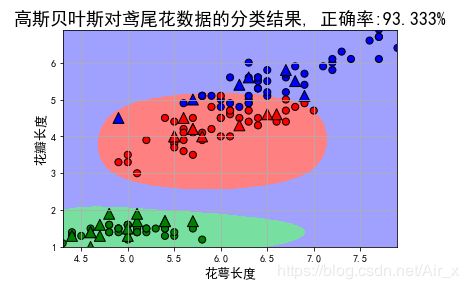
    def iris_classifier(self):
        # 花萼长度、花萼宽度，花瓣长度，花瓣宽度
        iris_feature_E = 'sepal length', 'sepal width', 'petal length', 'petal width'
        iris_feature_C = u'花萼长度', u'花萼宽度', u'花瓣长度', u'花瓣宽度'
        iris_class = 'Iris-setosa', 'Iris-versicolor', 'Iris-virginica'
        features = [0, 2]
        ## 读取数据
        path = '../datas/iris.data'  # 数据文件路径，也可以直接使用sklearn内的鸢尾花数据集
        data = pd.read_csv(path, header=None)
        x = data[list(range(4))]
        x = x[features]
        y = pd.Categorical(data[4]).codes  ## 直接将数据特征转换为0，1,2
        print("总样本数目：%d；特征属性数目：%d" % x.shape)
        ## 0. 数据分割，形成模型训练数据和测试数据
        x_train, x_test, y_train, y_test = train_test_split(x, y, train_size=0.8, random_state=14)
        print("训练数据集样本数目：%d, 测试数据集样本数目：%d" % (x_train.shape[0], x_test.shape[0]))
        ## 高斯贝叶斯模型构建
        clf = Pipeline([
            ('sc', StandardScaler()),  # 标准化，把它转化成了高斯分布
            ('clf', GaussianNB())])  
        ## 训练模型
        clf.fit(x_train, y_train)
        #计算准确度
        y_train_hat = clf.predict(x_train)
        print('训练集准确度: %.2f%%' % (100 * accuracy_score(y_train, y_train_hat)))
        y_test_hat = clf.predict(x_test)
        print('测试集准确度：%.2f%%' % (100 * accuracy_score(y_test, y_test_hat)))
        "画图"
        N, M = 500, 500  # 横纵各采样多少个值

        # 生成画图的图像区域
        x1_min1, x2_min1 = x_train.min()
        x1_max1, x2_max1 = x_train.max()
        x1_min2, x2_min2 = x_test.min()
        x1_max2, x2_max2 = x_test.max()
        x1_min = np.min((x1_min1, x1_min2))
        x1_max = np.max((x1_max1, x1_max2))
        x2_min = np.min((x2_min1, x2_min2))
        x2_max = np.max((x2_max1, x2_max2))

        t1 = np.linspace(x1_min, x1_max, N)
        t2 = np.linspace(x2_min, x2_max, N)
        x1, x2 = np.meshgrid(t1, t2)  # 生成网格采样点
        x_show = np.dstack((x1.flat, x2.flat))[0]  # 测试点

        cm_light = mpl.colors.ListedColormap(['#77E0A0', '#FF8080', '#A0A0FF'])
        cm_dark = mpl.colors.ListedColormap(['g', 'r', 'b'])
        y_show_hat = clf.predict(x_show)  # 预测值
        y_show_hat = y_show_hat.reshape(x1.shape)

        ## 画图
        plt.figure(facecolor='w')
        plt.pcolormesh(x1, x2, y_show_hat, cmap=cm_light)  # 预测值的显示
        plt.scatter(x_train[features[0]], x_train[features[1]], c=y_train, edgecolors='k', s=50, cmap=cm_dark)
        plt.scatter(x_test[features[0]], x_test[features[1]], c=y_test, marker='^', edgecolors='k', s=120, cmap=cm_dark)
        plt.xlabel(iris_feature_C[features[0]], fontsize=13)
        plt.ylabel(iris_feature_C[features[1]], fontsize=13)
        plt.xlim(x1_min, x1_max)
        plt.ylim(x2_min, x2_max)
        plt.title(u'高斯贝叶斯对鸢尾花数据的分类结果, 正确率:%.3f%%' % (100 * accuracy_score(y_test, y_test_hat)), fontsize=18)
        plt.grid(True)
        plt.show()
 
if __name__ == '__main__':
    NBayes = NBayes_sklearn()
    NBayes.iris_classifier()