【SVPWM】SVPWM算法推导及其Simulink仿真（一）

前言

有关原理部分请参照 SVPWM算法原理及详解 和 SVPWM的原理及法则推导和控制算法详解(他们的公式慎用，有些有坑，看原理就行了)。本文主要讲解七段式SVPWM的实现方法以及关键公式推导与其结果。本算法经过了Simulink仿真以及STM32F407ZGT6、STM32F334C8T6、STM32F334R8T6等途径验证。如果你不想了解原理，也可以跳过这些，直接看这篇文章 SVPWM的Simulink实现。

SVPWM生成流程

Created with Raphaël 2.2.0 开关周期开始 得到Uref与角度θ 判断扇区 计算三路PWM的占空比 开关周期结束

其中 U_ref 是期望电压矢量的模，角度$\theta$是它与$\alpha$轴的夹角。且
$$U_{ref}=\frac{m{U}_{dc}}{\sqrt{3}}$$
其中m是调制系数，当$m>1$时会过调制，波形失真。此时 U_ref 超出了图1中正六边形的内切圆范围。而U_ref的最大值就是非零电压矢量的值，为$\frac{2U_{dc}}{3}$。

图1

由于三项电压互差$120^{\circ }$，以其中一项为例，它的相电压调制函数和线电压调制函数（也就是SVPWM滤过波之后的）分别是：
$$U_a(\theta )=\{\begin{array}{ll}\frac{\sqrt{3}}{2}{U}_{ref}\cos (\theta -\frac{\pi }{6}),& 0\le \theta <\frac{\pi }{3},\pi \le \theta <\frac{4\pi }{3}\\ & \\ \frac{3}{2}{U}_{ref}\cos \left(\theta \right),& \frac{\pi }{3}\le \theta <\frac{2\pi }{3},\frac{4\pi }{3}\le \theta <\frac{5\pi }{3}\\ & \\ \frac{\sqrt{3}}{2}{U}_{ref}\cos (\theta +\frac{\pi }{6}),& \frac{2\pi }{3}\le \theta <\pi ,\frac{5\pi }{3}\le \theta <2\pi \end{array}$$
$$U_{ab}(\theta )=U_a(\theta )-U_b(\theta )=\sqrt{3}{U}_{ref}\sin \left(\theta +\frac{\pi }{3}\right)$$
因此SVPWM逆变器相电压最大幅值为$$\frac{\sqrt{3}}{2}\times \frac{2U_{dc}}{3}=\frac{U_{dc}}{\sqrt{3}}$$

从调制波函数来看，相电压输出的是不规则的分段函数，为马鞍波形。而线电压输出的则是正弦波形。

判断扇区

七段式 SVPWM 共有5个非零矢量和2个零矢量，这5个非零矢量将平面分成了6个扇区，如图所示。

图2

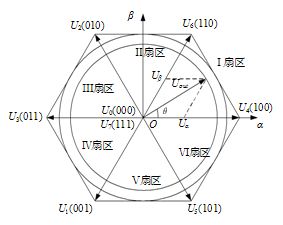
首先我们要根据 $U_{\alpha }$ 和 $U_{\beta }$ 判断出扇区N。由矢量图几何关系分析，可以判断出合成电压矢量 Uref 落在第 X扇区的充分必要条件,因此得出下表：

扇区	落在此扇区的充要条件
I	$U_{\alpha }>0$, $U_{\beta }>0$ 且 $\frac{U_{\beta }}{U_{\alpha }}<\sqrt{3}$
II	$U_{\beta }>0$ 且 $\frac{U_{\beta }}{|U_{\alpha }|}>\sqrt{3}$
III	$U_{\alpha }<0$, $U_{\beta }>0$ 且 $\frac{-U_{\beta }}{U_{\alpha }}<\sqrt{3}$
IV	$U_{\alpha }<0$, $U_{\beta }<0$ 且 $\frac{U_{\beta }}{U_{\alpha }}<\sqrt{3}$
V	$U_{\beta }<0$ 且 $\frac{-U_{\beta }}{|U_{\alpha }|}>\sqrt{3}$
VI	$U_{\alpha }>0$, $U_{\beta }<0$ 且 $\frac{-U_{\beta }}{U_{\alpha }}<\sqrt{3}$

进一步观察分析可得扇区N完全由$U_{\beta }，\sqrt{3}{U}_{\alpha }-U_{\beta },-\sqrt{3}{U}_{\alpha }-U_{\beta }$ 三个式子的正负来决定。因此若定义$$\{\begin{array}{l}{U}_1=U_{\beta }\\ U_2=\sqrt{3}{U}_{\alpha }-U_{\beta }\\ U_3=-\sqrt{3}{U}_{\alpha }-U_{\beta }\end{array}$$
且若

U ₁>0, A=1 , 否则 A=0;
U ₂>0, B=1 , 否则 B=0;
U ₃>0, C=1 , 否则 C=0;

可以看出 A，B，C 之间共有八种组合，但由判断扇区的公式可知 A，B，C 不会同时为 1 或同时为 0，所以实际的组合是六种，A，B，C 组合取不同的值对 应着不同的扇区，并且是一一对应的，因此完全可以由 A，B，C 的组合判断所在的扇区。为区别六种状态，令 N=4C+2B+A，则可以通过下表计算参考电压矢量 Uref 所在的扇区。

N	1	2	3	4	5	6
扇区	II	VI	I	IV	III	V

C语言实现：

#define Sqrt3 1.732050808f
void JudgeArea(svpwm_variables * svpwm_v)
{	
    //看不清楚可以删掉所有代码段中的'svpwm_v->' 
	char A,B,C,T;
	A = (svpwm_v->Ub)>0? 1:0;
	B = (Sqrt3*svpwm_v->Ua - svpwm_v->Ub)>0? 1:0;
	C = (-Sqrt3*svpwm_v->Ua - svpwm_v->Ub)>0? 1:0;
	T = A + 2*B +4*C;
	
	switch (T)
	{
		case 1: svpwm_v->N=2;break;
		case 2: svpwm_v->N=6;break;
		case 3: svpwm_v->N=1;break;
		case 4: svpwm_v->N=4;break;
		case 5: svpwm_v->N=3;break;
		case 6: svpwm_v->N=5;break;
		default: svpwm_v->N=1;break;
	}
}

计算占空比

计算每个扇区中基本矢量的持续时间

传统计算使用到了角度以及三角函数，较为繁琐，实际上利用$U_{\alpha },U_{\beta }$ 就可以得出结论。以扇区III为例，求解方程组后得出各矢量持续时间为$$T_2=T_K\frac{\sqrt{3}{U}_{\beta }}{U_{dc}}$$$$T_3=-T_K\frac{3U_{\alpha }+\sqrt{3}{U}_{\beta }}{2U_{dc}}$$$$T_0=T_7=\frac{T_K-T_2-T_3}{2}$$

其中T_K是开关周期。若计算出所有扇区的基矢持续时间发现如此可简化运算，定义
$$\{\begin{array}{l}X=\sqrt{3}{U}_{\beta }\\ Y=\frac{3U_{\alpha }+\sqrt{3}{U}_{\beta }}{2}\\ Z=\frac{-3U_{\alpha }+\sqrt{3}{U}_{\beta }}{2}\end{array}$$
再定义T_X是主矢量，T_Y是辅矢量（如I扇区中T_X=T₄，T_Y=T₆；III扇区中T_X=T₂，T_Y=T₃）。则可根据扇区N来简化计算：

扇区	I	II	III	IV	V	VI
TX	-Z	Y	X	Z	-Y	-X
TY	X	Z	-Y	-X	-Z	Y

C语言实现：

//已经定义过Sqrt3了
void CacuTime(svpwm_variables * svpwm_v)
{
	float x,y,z;
	float Dx,Dy,Dz;//Tz是零矢量持续时间比
	
	//你看我x y z的表达式里边已经把开关周期除了，实际上这是持续时间占开关周期的比例
	x = Sqrt3*svpwm_v->Ub;
	y = (3*svpwm_v->Ua +Sqrt3*svpwm_v->Ub)/2;
	z = (-3*svpwm_v->Ua +Sqrt3*svpwm_v->Ub)/2;
	
	switch(svpwm_v->N)
	{
		case 1: Dx = -z;Dy = x;break;
		case 2: Dx = y;Dy = z;break;
		case 3: Dx = x;Dy = -y;break;
		case 4: Dx = z;Dy = -x;break;
		case 5: Dx = -y;Dy = -z;break;
		case 6: Dx = -x;Dy = y;break;
		default:Dx = -z;Dy = x;break;
	}
	Dz = 1-(Dx+Dy);
}

计算三路占空比

为了尽量减少开关次数，这里的PWM的定时器模式使用了中心对称模式（有疑问可看这里边沿对齐PWM和中心对齐PWM）在这里我以扇区I、II、III为例说明三路PWM的占空比与扇区N计算规律。

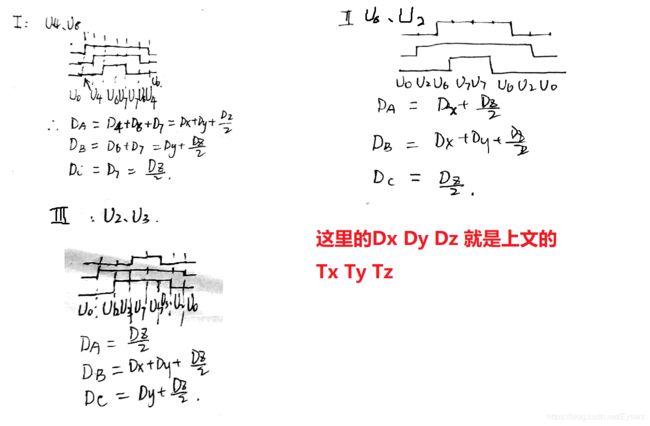
由于占空比是比例这里我把T_X、T_Y、T_Z同除以T_K，分别记为D_X、D_Y、D_Z可总结出规律如下：

扇区N	I	II	III	IV	V	VI
DutyA	Dx+Dy+Dz/2	Dx+Dz/2	Dz/2	Dz/2	Dy+Dz/2	Dx+Dy+Dz/2
DutyB	Dy+Dz/2	Dx+Dy+Dz/2	Dx+Dy+Dz/2	Dx+Dz/2	Dz/2	Dz/2
DutyC	Dz/2	Dz/2	Dy+Dz/2	Dx+Dy+Dz/2	Dx+Dy+Dz/2	Dx+Dz/2

C语言实现：

void CacuPWMDuty(svpwm_variables * svpwm_v)
{
	//Dx Dy Dz 已经由上一个函数计算得出
	switch(svpwm_v->N)
	{
		case 1: 
			svpwm_v->DutyA = Dx+Dy+Dz/2;
			svpwm_v->DutyB = Dy+Dz/2;
			svpwm_v->DutyC = Dz/2;
			break;
		case 2: 
			svpwm_v->DutyA = Dx+Dz/2;
			svpwm_v->DutyB = Dx+Dy+Dz/2;
			svpwm_v->DutyC = Dz/2;
			break;
		case 3:
			svpwm_v->DutyA = Dz/2;
			svpwm_v->DutyB = Dx+Dy+Dz/2;
			svpwm_v->DutyC = Dy+Dz/2;
			break;
		case 4: 
			svpwm_v->DutyA = Dz/2;
			svpwm_v->DutyB = Dx+Dz/2;
			svpwm_v->DutyC = Dx+Dy+Dz/2;
			break;
		case 5:
			svpwm_v->DutyA = Dy+Dz/2;
			svpwm_v->DutyB = Dz/2;
			svpwm_v->DutyC = Dx +Dy +Dz/2;
			break;
		case 6:
			svpwm_v->DutyA = Dx+Dy+Dz/2;
			svpwm_v->DutyB = Dz/2;
			svpwm_v->DutyC = Dx+Dz/2;
			break;
		default:svpwm_v->DutyA = Dx+Dy+Dz/2;svpwm_v->DutyB = Dy+Dz/2;svpwm_v->DutyC=Dz/2;break;
	}
}

其实到这就差不多了，实际操作生成SVPWM时还需要在每个开关周期的中断重新调用这几个函数。暂时想不到还有什么，想到了再补充。