KNN 算法

01 场景代入

在一个酒吧里，吧台上摆着十杯几乎一样的红酒，老板跟你打趣说想不想来玩个游戏，赢了免费喝酒，输了付 3 倍酒钱，赢的概率有 50%。你是个爱冒险的人，果断说玩。

老板接着道：你眼前的这十杯红酒，每杯略不相同，前五杯属于「赤霞珠」，后五杯属于「黑皮诺」。现在，我重新倒一杯酒，你只需要根据刚才的十杯正确地告诉我它属于哪一类。

听完你有点心虚：根本不懂酒啊，光靠看和尝根本区分辨不出来，不过想起自己是搞机器学习的，不由多了几分底气爽快地答应了老板。

你没有急着品酒而是问了老板每杯酒的一些具体信息：酒精浓度、颜色深度等，以及一份纸笔。老板一边倒一杯新酒，你边疯狂打草稿。很快，你告诉老板这杯新酒应该是「赤霞珠」。

老板瞪大了眼下巴也差点惊掉，从来没有人一口酒都不尝就能答对，无数人都是反复尝来尝去，最后以犹豫不定猜错而结束。你神秘地笑了笑，老板信守承诺让你开怀畅饮。微醺之时，老板终于忍不住凑向你打探是怎么做到的。

02 kNN 算法介绍

学会 kNN 算法，只需要三步：

• 了解 kNN 算法思想
• 掌握它背后的数学原理
• 最后用简单的 Python 代码实现

在说 kNN 算法前说两个概念：样本和特征。

上面的每一杯酒称作一个「样本」，十杯酒组成一个样本集。酒精浓度、颜色深度等信息叫作「特征」。这十杯酒分布在一个多维特征空间中。说到空间，我们最多能感知三维空间，为了理解方便，我们假设区分赤霞珠和黑皮诺，只需利用：酒精浓度和颜色深度两个特征值。这样就能在二维坐标轴来直观展示。

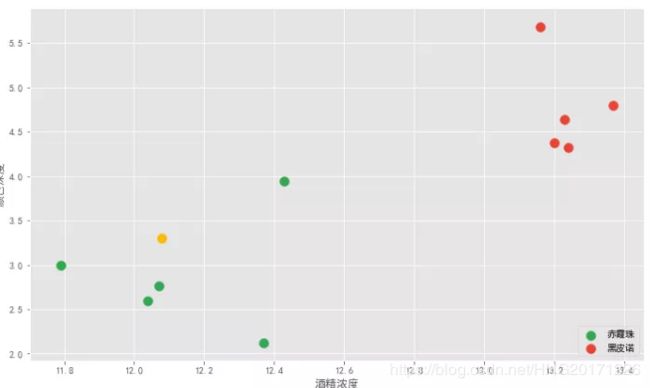
横轴是酒精浓度值，纵轴是颜色深度值。十杯酒在坐标轴上形成十个点，绿色的 5 个点代表五杯赤霞珠，红色的 5 个点代表五杯黑皮诺。可以看到两类酒有明显的界限。老板新倒的一杯酒是图中黄色的点。
要确定这杯酒是赤霞珠还是黑皮诺，答案显而易见，通过主观距离判断它应该属于赤霞珠。

这就用到了 K 近邻算法思想。该算法首先需要取一个参数 K，机器学习中给的经验取值是 3，我们假设先取 3 ，具体取多少以后再研究。对于每个新来的点，K 近邻算法做的事情就是在所有样本点中寻找离这个新点最近的三个点，统计三个点所属类别然后投票统计，得票数最多的类别就是新点的类别。

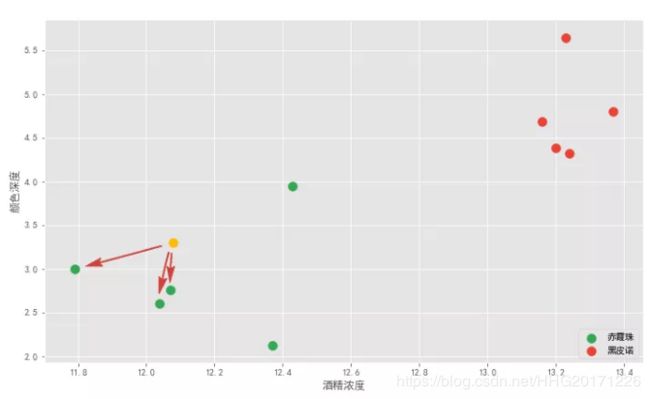
上图有绿色和红色两个类别。离黄色最近的 3 个点都是绿点，所以绿色和红色类别的投票数是 3:0 ，绿色取胜，所以黄色点就属于绿色，也就是新的一杯就属于赤霞珠。

这就是 K 近邻算法，它的本质就是通过距离判断两个样本是否相似，如果距离够近就觉得它们相似属于同一个类别。当然只对比一个样本是不够的，误差会很大，要比较最近的 K 个样本，看这 K 个 样本属于哪个类别最多就认为这个新样本属于哪个类别。

再举一例，老板又倒了杯酒让你再猜，你可以在坐标轴中画出它的位置。离它最近的三个点，是两个红点和一个绿点。红绿比例是 2:1，红色胜出，所以 K 近邻算法告诉我们这杯酒大概率是黑皮诺。

可以看到 K 近邻算法就是通过距离来解决分类问题。这里我们解决的二分类问题，事实上 K 近邻算法天然适合解决多分类问题，除此之外，它也适合解决回归问题，之后一一细讲。

03 Python 代码实现

首先随机设置十个样本点表示十杯酒，我这里取了 Sklearn 中的葡萄酒数据集的部分样本点，这个数据集在之后的算法中会经常用到会慢慢介绍。

import numpy as np
import matplotlib.pyplot as plt
from math import sqrt

X_raw = [[14.23,  5.64],
         [13.2 ,  4.38],
         [13.16,  5.68],
         [14.37,  4.80 ],
         [13.24,  4.32],
         [12.07,  2.76],
         [12.43,  3.94],
         [11.79,  3.  ],
         [12.37,  2.12],
         [12.04,  2.6 ]]

y_raw = [0, 0, 0, 0, 0, 1, 1, 1, 1, 1]

X_raw 的两列值分别是颜色深度和酒精浓度值，y_raw 中的 0 表示黑皮诺，1 表示赤霞珠。
新的一杯酒信息：

x_test = np.array([12.8,4.1])

在机器学习中常使用 numpy 的 array 数组而不是列表 list，因为 array 速度快也能执行向量运算，所以在运算之前先把上面的列表转为数组：

X_train = np.array(X_raw)
y_train = np.array(y_raw)

有了 X Y 坐标就可以绘制出第一张散点图：

plt.style.use('ggplot')
plt.figure(figsize=(10, 6))

plt.scatter(X_train[y_train==1,0],X_train[y_train==1,1],s=100,color='g',label='赤霞珠')
plt.scatter(X_train[y_train == 0, 0], X_train[y_train == 0, 1], s=100, color='r', label='黑皮诺')
plt.scatter(x_test[0],x_test[1],s=100,color='y') # x_test

接着，根据欧拉公式计算黄色的新样本点到每个样本点的距离：

distances = [sqrt(np.sum((x - x_test)**2)) for x in X_train] # 列表推导式
print(distances)
'''
[2.101547049199708, 0.4882622246293471, 1.6204937519163718, 
1.7189822570346662, 0.49193495504995355, 1.5259423318068084, 
0.4031128874149283, 1.4933519344079622, 2.026153992173349, 1.6815469068687918]

'''

这样就计算出了黄色点到每个样本点的距离，接着找出最近的 3 个点，可以使用 np.argsort函数返回样本点的索引位置：

sort = np.argsort(distances)
print(sort)

通过这个索引值就能在 y_train 中找到对应酒的类别，再统计出排名前 3 的就行了：

K=3

topK=[y_train[i] for i in sort[:K]]
print(topK)
#[1, 0, 0]

可以看到距离黄色点最近的 3 个点都是绿色的赤霞珠，与刚才肉眼观测的结果一致。

到这里，距离输出黄色点所属类别只剩最后一步，使用 Counter 函数统计返回类别值即可：

from collections import Counter
votes = Counter(topK)
votes
[out]：Counter({1: 3})

predict_y = votes.most_common(1)[0][0]
predict_y
[out]：1

最后的分类结果是 1 ，也就是新的一杯酒是赤霞珠。

04 sklearn 调包

from sklearn.neighbors import KNeighborsClassifier 
kNN_classifier = KNeighborsClassifier(n_neighbors=3)
kNN_classifier.fit(X_train,y_train )
x_test = x_test.reshape(1,-1)
kNN_classifier.predict(x_test)[0]

[out]：1

首先从 sklearn 中引入了 kNN 的分类算法函数 KNeighborsClassifier 并建立模型，设置最近的 K 个样本数量 n_neighbors 为 3。接下来 fit 训练模型，最后 predict 预测模型得到分类结果 1，和我们刚才手写的代码结果一样的。

用 Python 一步步写出 Sklearn 中的 kNN 封装算法。

虽然调用 Sklearn 库算法，简单的几行代码就能解决问题，感觉很爽，但其实我们时处于黑箱中的，Sklearn 背后干了些什么我们其实不明白。作为初学者，如果不搞清楚算法原理就直接调包，学的也只是表面功夫，没什么卵用。

from sklearn.neighbors import KNeighborsClassifier 
kNN_classifier = KNeighborsClassifier(n_neighbors=3)
kNN_classifier.fit(X_train,y_train )
x_test = x_test.reshape(1,-1)
kNN_classifier.predict(x_test)[0]

[out]：1

可以说，Sklearn 调用所有的机器学习算法几乎都是按照这样的套路：把训练数据喂给选择的算法进行 fit 拟合，能计算出一个模型，模型有了就把要预测的数据喂给模型，进行预测 predict，最后输出结果，分类和回归算法都是如此。

值得注意的一点是，kNN 是一个特殊算法，它不需要训练（fit）建立模型，直接拿测试数据在训练集上就可以预测出结果。这也是为什么说 kNN 算法是最简单的机器学习算法原因之一。

但在上面的 Sklearn 中为什么这里还 fit 拟合这一步操作呢，实际上是可以不用的，不过 Sklearn 的接口很整齐统一，所以为了跟多数算法保持一致把训练集当成模型。

代码整理成一个函数就可以看到没有训练过程：

 import numpy as np
 from math import sqrt
 from collections import Counter
 
 def kNNClassify(K, X_train, y_train, X_predict):
     distances = [sqrt(np.sum((x - X_predict)**2)) for x in X_train]
     sort = np.argsort(distances)
     topK = [y_train[i] for i in sort[:K]]
     votes = Counter(topK)
     y_predict = votes.most_common(1)[0][0]
     return y_predict

接下来我们按照上图的思路，把 Sklearn 中封装的 kNN 算法，从底层一步步写出那 5 行代码是如何运行的：

 import numpy as np
 from math import sqrt
 from collections import Counter
 
 class kNNClassifier:
     def __init__(self,k):
         self.k =k
         self._X_train = None
         self._y_train = None

     def fit(self,X_train,y_train):
         self._X_train = X_train
         self._y_train = y_train
         return self

首先，我们需要把之前的函数改写一个名为 kNNClassifier 的 Class 类，因为 Sklearn 中的算法都是面向对象的，使用类更方便。
在__init__函数中定义三个初始变量，k 表示我们要选择传进了的 k 个近邻点。
self._X_train和 self._y_train前面有个 下划线_ ，意思是把它们当成内部私有变量，只在内部运算，外部不能改动。
接着定义一个 fit 函数，这个函数就是用来拟合 kNN 模型，但 kNN 模型并不需要拟合，所以我们就原封不动地把数据集复制一遍，最后返回两个数据集自身。
这里要对输入的变量做一下约束，一个是 X_train 和 y_train 的行数要一样，一个是我们选的 k 近邻点不能是非法数，比如负数或者多于样本点的数， 不然后续计算会出错。用什么做约束呢，可以使用 assert 断言语句：

def fit(self,X_train,y_train):
        assert X_train.shape[0] == y_train.shape[0],"添加 assert 断言是为了确保输入正常的数据集和k值，如果不添加一旦输入不正常的值，难找到出错原因"
        assert self.k <= X_train.shape[0]
        self._X_train = X_train
        self._y_train = y_train
        return self

接下来我们就要传进待预测的样本点，计算它跟每个样本点之间的距离，对应 Sklearn 中的 predict ，这是算法的核心部分。而这一步代码就是我们之前写的函数，可以直接拿过来用，加几行断言保证输入的变量是合理的。

 def predict(self,X_predict):
         assert self._X_train is not None,"要求predict 之前要先运行 fit 这样self._X_train 就不会为空"
         assert self._y_train is not None
         assert X_predict.shape[1] == self._X_train.shape[1],"要求测试集和预测集的特征数量一致"
 
         distances = [sqrt(np.sum((x_train - X_predict)**2)) for x_train in self._X_train]
         sort = np.argsort(distances)
         topK = [self._y_train[i] for i in sort[:self.k]]
         votes = Counter(topK)
         y_predict = votes.most_common(1)[0][0]
         return y_predict

到这儿我们就完成了一个简易的 Sklearn kNN 封装算法，保存为kNN_sklearn.py文件，然后在 jupyter notebook 运行测试一下：
先获得基础数据：

 # 样本集
 X_raw = [[13.23,  5.64],
        [13.2 ,  4.38],
        [13.16,  4.68],
        [13.37,  4.8 ],
        [13.24,  4.32],
        [12.07,  2.76],
        [12.43,  3.94],
        [11.79,  3.  ],
       [12.37,  2.12],
       [12.04,  2.6 ]]
X_train = np.array(X_raw)

# 特征值
y_raw = [0, 0, 0, 0, 0, 1, 1, 1, 1, 1]
y_train = np.array(y_raw)

# 待预测值
x_test= np.array([12.08,  3.3])
X_predict = x_test.reshape(1,-1) 

注意：当预测变量只有一个时，一定要 reshape(1,-1) 成二维数组不然会报错。

再进一步，如果我们一次预测不只一个点，而是多个点，比如要预测下面这两个点属于哪一类：

那能不能同时给出预测的分类结果呢？答案当然是可以的，我们只需要稍微修改以下上面的封装算法就可以了，把 predict 函数作如下修改：

 def predict(self,X_predict):
         y_predict = [self._predict(x) for x in X_predict]  # 列表生成是把分类结果都存储到list 中然后返回
         return np.array(y_predict)
 
 def _predict(self,x):  # _predict私有函数
         assert self._X_train is not None
         assert self._y_train is not None
 
         distances = [sqrt(np.sum((x_train - x)**2)) for x_train in self._X_train]
         sort = np.argsort(distances)
         topK = [self._y_train[i] for i in sort[:self.k]]
         votes = Counter(topK)
         y_predict = votes.most_common(1)[0][0]
         return y_predict

这里定义了两个函数，predict 用列表生成式来存储多个预测分类值，预测值从哪里来呢，就是利用_predict函数计算，_predict前面的下划线同样表明它是封装的私有函数，只在内部使用，外界不能调用，因为不需要。

算法写好，只需要传入多个预测样本就可以了，这里我们传递两个：

X_predict = np.array([[12.08,  3.3 ],
        [12.8,4.1]])

到这里，我们就按照 Sklearn 算法封装方式写出了 kNN 算法，不过 Sklearn 中的 kNN 算法要比这复杂地多，因为 kNN 算法还有很多要考虑的，比如处理 kNN 算法的一个缺点：计算耗时。简单说就是 kNN 算法运行时间高度依赖样本集有和特征值数量的维度，当维度很高时算法运行时间就极速增加，具体原因和改善方法我们后续再说。

现在还有一个重要的问题，我们在全部训练集上实现了 kNN 算法，但它预测的效果和准确率怎么样，我们并不清楚，下一篇文章，来说说怎么衡量 kNN 算法效果的好坏。

Sklearn 划分训练集和测试集

通过以上两篇我们就初步学会了 kNN 算法。不过在对算法做预测时，使用了全部数据作为训练集，这样一来算法的预测准确率如何并不清楚。

所以我们做了改进，将数据集拆成一大一小两部分，大的作为训练集，小的作为测试集。在训练集上训练好 kNN 模型后，把测试集喂给它得到预测结果，接着和测试集本身的真实标签值作比较，得到了模型的准确率。

这一过程用到了 sklearn 的 train_test_split 方法，最终将一份有 178 个样本的葡萄酒数据集，按照 7:3 的比例随机划分出了 124 个训练样本和 54 个测试样本。

预测方法我们使用了两种，一种是根据欧拉公式逐步手写，思路清晰直观。另外一种方法是模仿 Sklearn 中的 kNN 算法，把代码封装起来以调用库的形式使用，更加精简。

然而这样做忽略了一个重要的问题，我们把全部的红酒样本都拿来生成 kNN 模型进行预测。而模型预测的准确率怎么样，并不清楚也无从验证。这在实际运用中有很大问题，比如说，根据股市数据做了一个模型，然后就直接参照这个模型就去投资股票了，结果模型预测趋势跟实际走势大相径庭，那就惨了。

所以我们希望生成一个模型后，能有一个测试集先来测试一下模型，看看效果怎么样，然后进一步地调整并生成一个尽可能好的模型。

这样的话，就需要把原始样本分成一大一小两份，比如 70% 和 30%，大的一份用来训练（train）生成模型，一份用来最后测试（test）模型。因为测试集本身有标签参照，跟模型预测的标签一对比就能知道模型效果如何。

下面我们仍然以葡萄酒数据集为例，把数据集划分为训练集和测试集建立模型，最后测试模型效果。

这份葡萄酒数据集来源于1988 年意大利的葡萄酒产地，属于 sklearn 自带的分类数据集，Sklearn 自带好几个常用的分类和回归数据集，之后会一一拿来做例子。

这份数据集包含 178 个样本，13 个数值型特征：alcohol酒精浓度、color_intensity 颜色深度等（我们在第一课就使用了这两个特征）。
标签（y值） 是葡萄酒的 3 种分类，用 [0,1,2] 表示。

加载数据集

样本 X 是 178 行 13 列的矩阵，标签 y 是一个 178 元素的向量，接下来准备划分训练集和测试集。

Sklearn 调包划分数据集

先来调用 Sklearn 数据集划分函数train_test_split：

test_size 是测试集比例，random_state 是一个随机种子，保证每次运行都能得到一样的随机结果

Sklearn 只用两行代码就可以划分好数据集，虽然简单但是它背后是怎么划分的我们并不清楚，为此，下面来手写一下以更好理解。

手写 train_test_split 函数

观察到原始数据集的标签值是从 0 到 2 有序排列的，所以不能直接划分，要先把数据集打乱保证随机抽样。打乱可以用 numpy 的 permutation 函数，它会返回打乱后的数据集的索引，这个函数的妙处就在于根据索引就能同时匹配到 X 和 y。二者是一一对应的
数据集整体打乱后设置一个划分比例，比如 0.3，表示测试集和训练集的比例是 0.7:0.3，结合索引就分别能得到训练样本和标签的数量。

因 Sklearn 中的 train_test_split 是向上取整，所以为了保持一致使用了向上取整的 ceil 函数，ceil (3.4) = 4；int 虽然也可以取整但它是向下取整的， int (3.4) = 3。
在打乱数据之前，添加了一行 random.seed (321) 函数，它的作用是保证重新运行时能得到相同的随机数，若不加这句代码，每次得到的结果都会不一样，不便于相互比较。

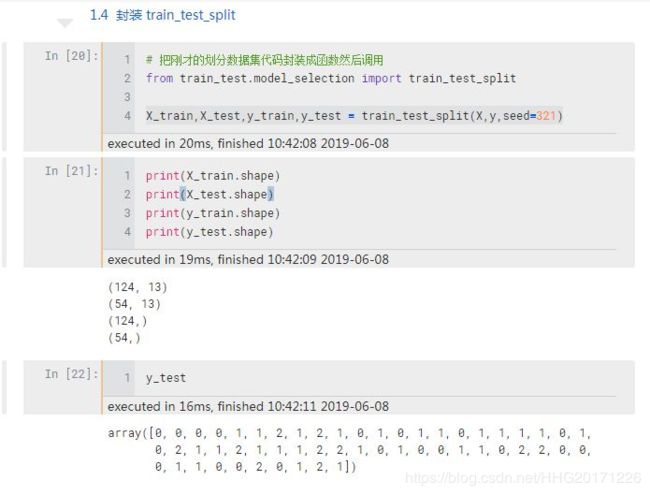
封装 train_test_split 函数

 import numpy as np
 from math import ceil
 
 def train_test_split(X, y, test_ratio=0.3, seed= None):
     assert X.shape[0] == y.shape[0], 'X y 的行数要一样'
     if seed:
         np.random.seed(seed)
     shuffle_index = np.random.permutation(len(X))
     test_size = ceil(len(X) * test_ratio)
     test_index = shuffle_index[:test_size]
     train_index = shuffle_index[test_size:]
     X_train = X[train_index]
     X_test = X[test_index]
     y_train = y[train_index]
     y_test = y[test_index]
     return X_train, X_test, y_train, y_test

这里添加了一个 assert 断言保证 X y 的行数一致。train_test_split 函数有四个参数：

test_ratio 是测试集比例，设置了一个默认值 0.3，意思就是当在 jupyter notebook 中调用这个函数的时候如果不指定该参数，它会默认设置为 0.3，如果想换一个比例了，手动设置这个参数就可以了。

seed = None 的意思是提供了一个随机种子选项，如果对随机结果没有要求，那么使用默认的 None 就可以，如果想固定一个随机结果，那么就需要设置该参数，比如前面我们设置了一个 321 ，任何一个数都可以，每个数的得出的随机结果不一样。

接着，将程序命名为 model_selection.py文件（跟 Sklearn 保持一致）存储到 .ipynb 目录的文件夹中，然后调用该函数即可。