图算法-最大流的应用
1.二分匹配问题
二分图 G=(V, E)为一个无向图,它的结点集合可以被划分为V=X并Y,并具有一下性质:每条边e都有一个端点在X中且另一个端点在Y中
G中的一个匹配是边的子集M属于E,使得某个结点至多出现在M中的一条边上
二分匹配问题即寻找G中最大规模的匹配
构建二分图G对应的流网络,G‘=(V’, E’), 其中V’ = V 并 {s,t}, 且:
![]()
E’中每条边赋单位容量

定理 G中最大匹配的基数等于G’中最大流的值,并且G中这样一个匹配中的边就是在G’中从X到Y的携带流的边
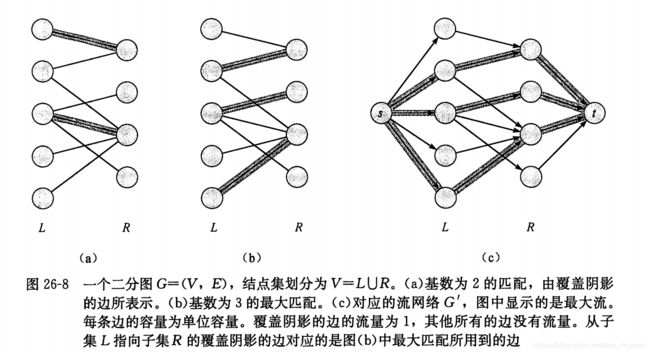
完美匹配
判断有完美匹配如果分成X与Y两边的二分图G=(V, E)有一个完美匹配,那么对所有S属于X,都有|N(S)| >= |S|
判断没有完美匹配-Hall定理假定二分图G=(V, E)分成两边X,Y使得|X| = |Y|, 那么图G或者有一个完美匹配,或者存在一个子集A属于X使得|N(A)| < |A| ,一个完美匹配或者一个适应的子集可以在O(mn)时间内找到
使用Ford-Fulkerson算法可判断是否具有完美匹配:
假定|X| = |Y| = x, 若不具有完美匹配,则G’的最大流值小于n, 则G’存在一个容量小于n的割(A’, B’), 令A=X交A’, 则A具有上一定理所述性质
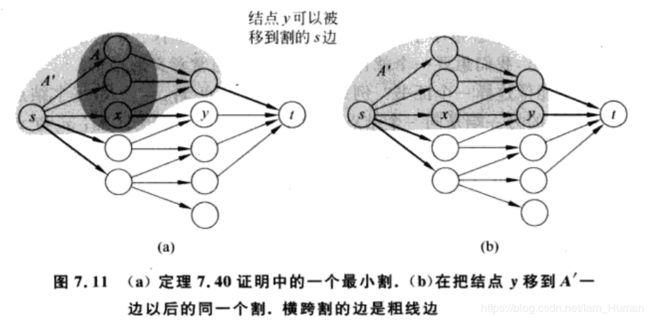
2.不交路径
称一组路径是边不交的,如果没有两条路径共享同一条边(但可能通过相同结点), 有向的边不交路径问题是在有向图G中找出边不交的s-t路径的最大数目,无向的边不交路径问题是在无向图G中找出边不交的s-t路径的最大数目
图G的s-t流:由图G及其两个不同结点s和t定义一个流网络,s为源结点,t为汇点,每条边容量为1, 图G的s-t流为该流网络的流
有向的边不交路径问题:
Menger定理在有向图G中从s到t存在k条边不交路径当且仅当在G中s-t流的最大值至少是k
(理解:若G中s-t的最大流为k,当且仅当 G中从s到t的不交路径的最大数目为k)
(Hall定理是Menger定理的特殊情况,Menger定理是最大流最小割定理的特殊情况)
无向图:
无向图->有向图, 将无向边(u, v)改为有向边
对于一种特例:
定理在无向图G中存在k条从s到t的边不交路径,当且仅当在G对应的有向图G’中s-t流的最大值至少是k,使用Ford-Fulkerson算法在O(mn)时间内可以找到无向图G中的一组最大的边不交的s-t路径
3.图像分割
问题描述
对一张图像的每个像素进行前景/背景分割,其中每个像素具有前景概率a_i, 背景概率b_i, 同时,相邻的像素称为邻居,对于互为邻居的像素对(i, j),其中一个分为前景而另一个分为背景存在分离罚分p_ij>0
分割问题即找到一个把像素集分为前景集合A与背景集合B的划分,使得下式最大:
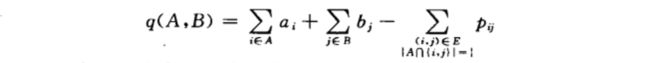
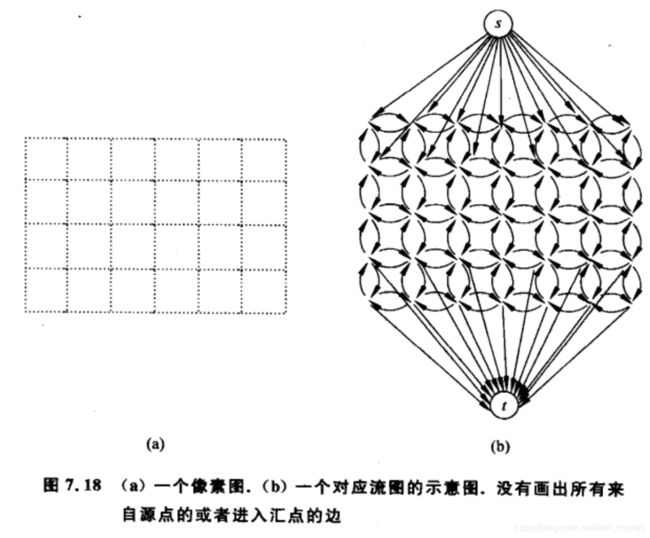
解决问题
转换:
- 将最优化目标转换为最小化目标:令Q=(a_i + b_i)在i上所有和,最优化目标改为最小化:其等价与最大化上述目标
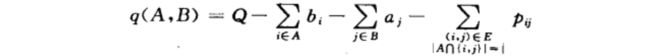
- 缺少原点与汇点: 添加超源结点s(代表前景)与超汇点t(代表背景),并与每个像素结点链接
- 无向化有向:无向边改为两条方向相反的有向边
综上:
由原像素图G及参数a_i, b_i, p_ij, 构造下列流网络G’=(V’, E’)
V’ = V并{s, t}
对每个像素i, 添加有向边(s, i), 其容量为a_i, 添加有向边(i, t), 其容量为b_i
对每队邻居(i, j), 添加有向边(i, j)与(j, i), 均具有容量p_ij
则,该流网络G’的一个s-t割对应于G的一个A, B划分,且割的值等于上述最小化目标
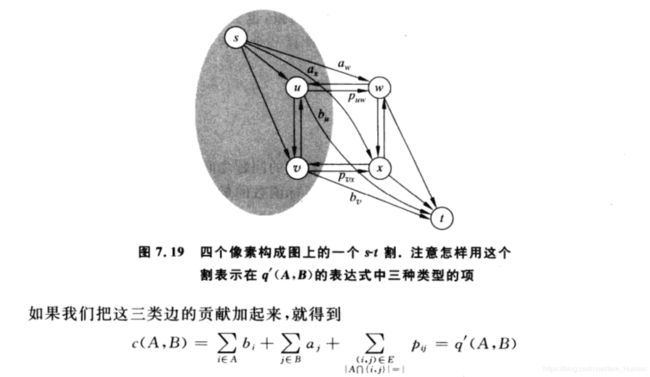
结论
通过解如上构造的图G’中的最小割, 得到最小割(A’, B’), 令A=A’-{s}, B=B’-{t}(即分别减去源结点与汇点), (A, B)即为上述图像分割问题的解,即令分段值q(A, B)最大化