寻路算法：找到NPC最好的行走路径

引言：寻路就是一个看似简单问题的解：给定点A 和B，AI 该怎么智能地在游戏世界中行走？这个问题的复杂来自于实际上A 和B 之间存在大量的路径可走，但只有一条是最佳的。只是找到一条两点之间的有效路径是不够的。理想的寻路算法需要查找所有可能的情况，然后比较出最好的路径。
本文将从搜索空间，可接受的启发式算法、贪婪最佳优先算法进行探讨。

搜索空间的表示

最简单的寻路算法设计就是将图作为数据结构。一个图包含了多个节点，连接任意邻近的点组成边。在内存中表示图有很多种方法，但是最简单的是邻接表。在这种表示中，每个节点包含了一系列指向任意邻近节点的指针。图中的完整节点集合可以存储在标准的数据结构容器里。下图演示了简单的图的可视化形象和数据表示。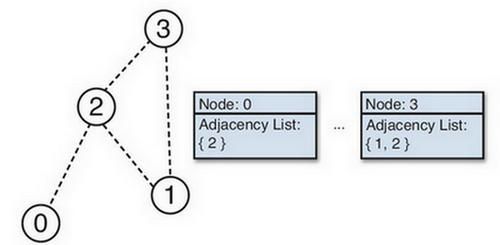

这意味着在游戏中实现寻路的第一步是如何将游戏世界用图来表示。这里有多种方法。一种简单的方法就是将世界分区为一个个正方形的格子（或者六边形）。在这种情况下，邻近节点就是格子中邻近的正方形。这个方法在回合制策略游戏中很流行，比如《文明》或者XCOM。

但是，对于实时动作游戏，NPC 通常不是在网格上一个正方形一个正方形地走。由此，在主流游戏中要么使用路点要么使用导航网格。上面两种方法，都可以手工在场景编辑器中构造数据。
但是手工输入数据不仅烦琐而且容易出错，所以大多数引擎都会让这个过程自动化。自动生成数据的算法超出了本书的范围，但是更多的信息可以在本书的参考资料中找到。
寻路节点最早在第一人称射击游戏（FPS）中使用，由id Software 在20 世纪90 年代早期推出。通过这种表示方法，关卡设计师可以在游戏世界中摆放那些AI 可以到达的位置。这些路点直接被解释为图中的节点。而边则可以自动生成。比如让设计师手动将节点组合在一起，可以自动处理判断两个点之间是否有障碍。如果没有障碍，那么边就会在两点之间生成。
路点的主要缺点是AI 只能在节点和边缘的位置移动。这是因为即使路点组成三角形，也不能保证三角形内部就是可以行走的。通常会有很多不能走的区域，所以寻路算法需要认为不在节点和边缘上的区域都是不可走的。
实际上，当部署路点之后，游戏世界中就会要么有很多不可到达的区域要么有很多路点。前者是不希望出现的状况，因为这样会让AI 的行为显得不可信而且不自然。而后者缺乏效率。越多的节点就会有越多的边缘，寻路算法花费的时间就会越长。通过路点，在性能和精确度上需要折中。
一个可选的解决方案就是使用导航网格。在这种方法中，图上的节点实际上就是凸多边形。邻近节点就是简单的任意邻近的凸多边形。这意味着整个游戏世界区域可以通过很少数量的凸多边形表示，结果就是图上的节点特别少。下图所示的是用游戏中同一个房间同时表示为路点和导航网格的结果比较。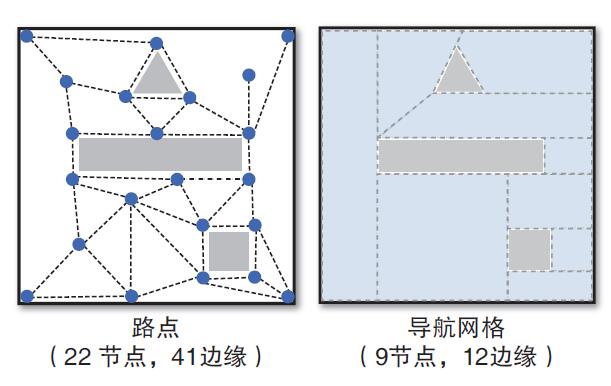

通过导航网格，在凸多边形内部的任意位置都认为是可走的。这意味着AI 有了大量的空间可以行走，因此寻路可返回更自然的路径。
导航网格还有其他一些优点。假设游戏中有牛和小鸡在农场中行走。由于小鸡比牛小很多，因此有一些区域只有小鸡可到达，而牛却不行。如果这个游戏使用路点，它通常需要两份图：每份图对应一种生物。这样，牛只能在自己相应的路点行走。与之相反，由于导航网格中每个节点都是凸多边形，计算牛能否进入不会花太多时间。因此，我们可以只用一份导航网格，并且计算哪些地方牛可以到达。
还有一点就是导航网格完全可以自动生成，这也是今天为什么使用路点的游戏越来越少的原因。比如说，多年来虚幻引擎使用路点作为寻路空间的表示。其中一款使用路点的虚幻引擎的游戏就是《战争机器》。而且，最近几年的虚幻引擎已经使用导航网格替代路点。在后来的《战争机器》系列，比如《战争机器3》就使用的是导航网格，这个转变引起工业上大量转用导航网格。
话虽这么说，但是寻路空间的表示并不完全会影响寻路算法的实现。在本节中的后续例子中，我们会使用正方形格子来简化问题。但是寻路算法仍不关心数据是表示为正方形格子、路点，或是导航网格。

可接受的启发式算法

所有寻路算法都需要一种方法以数学的方式估算某个节点是否应该被选择。大多数游戏都会使用启发式，以ℎ(x) 表示，就是估算从某个位置到目标位置的开销。理想情况下，启发式结果越接近真实越好。如果它的估算总是保证小于等于真实开销，那么这个启发式是可接受的。如果启发式高估了实际的开销，这个寻路算法就会有一定概率无法发现最佳路径。对于正方形格子，有两种方式计算启发式。

曼哈顿距离是一种在大都市估算城市距离的方法。某个建筑可以有5 个街区远，但不必真的有一条路长度刚好为5 个街区。
曼哈顿距离认为不能沿对角线方向移动，因此也只有这种情况下才能使用启发式。如果对角线移动是被允许的，则曼哈顿距离会经常高估真实开销。
在2D 格子中，曼哈顿距离的计算如下：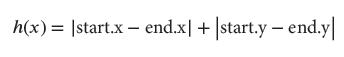

第二种计算启发式的方法就是欧几里得距离。这种启发式的计算使用标准距离公式然后估算直线路径。不像曼哈顿距离，欧几里得距离可以用在其他寻路表示中计算启发式，比如路点或者导航网格。在我们的2D 格子中，欧几里得距离为：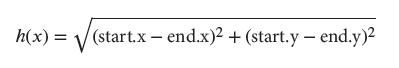

贪婪最佳优先算法

在有了启发式之后，可以开始实现一个相对简单的算法：贪婪最佳优先算法。一个算法如果没有做任何长期计划而且只是马上选择最佳答案的话，则可以被认为是贪婪算法。在贪婪最佳优先算法的每一步，算法会先看所有邻近节点，然后选择最低开销的启发式。
虽然这样看起来理由充足，但是最佳优先算法通常得到的都是次优的路径。看看下图中的表示。绿色正方形是开始节点，红色正方形是结束节点，灰色正方形是不可穿越的。箭头表示贪婪最佳优先算法的路径。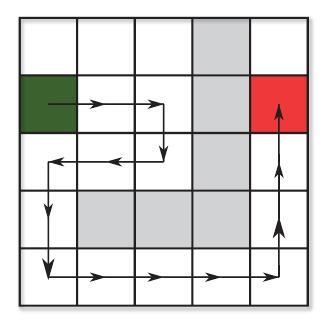

路径上存在不必要的向右移动，这是因为这在当时就是最佳的访问节点。一个理想的路径应该是一开始就往下走，但是这要求一定程度的计划，这是贪婪算法所不具备的。大多数游戏都需要比贪婪最佳优先算法所能提供的更好的寻路。但是本章后续的寻路算法都基于贪婪最佳优先算法，所以先理解贪婪算法才能往下继续，先看看如何实现这个贪婪算法。
首先，先看看我们每个节点所需要存储的数据。为了能够将这些数据构造成图，需要有额外的邻近信息。对于这个算法，我们只要一些额外的数据：

struct Node
    Node parent
    float h
end

那个parent 成员变量用于跟踪哪个节点是当前访问的。注意到像C++ 那样的语言，parent可能是个指针，而在其他语言中（比如C#），类可能天然地以引用传递。parent 成员的价值在于构造链表，能够从终点回到起点。当算法完成的时候，parent 链表就可以通过遍历得到最终路径。
浮点数h 存储了某个节点的ℎ(x) 的值，这个值导致在选择节点的时候会偏向于h 值最小的节点。
算法的下一个组件就是用于临时存储节点的容器：开放集合和封闭集合。开放集合存储了所有目前需要考虑的节点。由于找到最低ℎ(x) 值开销节点的操作是很常见的，所以对于开放集合可以采用某种类似于二叉堆或者优先级队列的容器。
而封闭集合则包含了所有已经被算法估值的节点。一旦节点在封闭集合中，算法不再对其进行考虑。由于经常会检查一个节点是否存在于封闭集合里，故会使用搜索的时间复杂度优于o(n) 的数据结构，比如二叉搜索树。
现在我们就有了贪婪最佳优先算法所需要的组件。假设有开始节点和结束节点，而且我们需要计算两点之间的路径。算法的主要部分在循环中处理，但是，在进入循环之前，我们需要先初始化一些数据：

currentNode = startNode
add currentNode to closedSet

当前节点只是跟踪哪个邻居节点是下一个估值的节点。在算法开始的时候，我们除了开始节点没有任何节点，所以需要先对开始节点的邻居进行估值。
在主循环里，我们首先要做的事情就是查看所有与当前节点相邻的节点，而且把一部分加到开放集合里：

do
    foreach Node n adjacent to currentNode
        if closedSet contains n
            continue
        else
        n.parent = currentNode
        if openSet does not contain n
            compute n.h
            add n to openSet
        end
    end
loop // 结束循环

注意任意已经在封闭集合里的节点都会被忽略。在封闭集合里的节点都在之前进行了估值，所以不需要再进一步估值了。对于其他相邻节点，这个算法会把parent 设置为当前节点。然后，如果节点不在开放集合中，我们计算ℎ(x) 的值并且把节点加入开放集合。
在邻近节点处理完之后，我们再看看开放集合。如果开放集合中再也没有节点存在，意味着我们把所有节点都估算过了，这就会导致寻路失败。实际上也不能保证总有路径可走，所以算法必须考虑这种情况：

if openSet is empty
    break // 退出主循环
end

但是，如果开放集合中还有节点，我们就可以继续。接下来要做的事情就是在开放集合中找到最低ℎ(x) 值开销节点，然后移到封闭集合中。在新一轮迭代中，我们依旧将其设为当前节点。

currentNode = Node with lowest h in openSet
remove currentNode from openSet
add currentNode to closedSet

这也是为什么有一种合适的容器能让开放集合变得简单。比起做o(n) 复杂度的搜索，二叉堆能够以o(1) 时间找到最低ℎ(��) 值节点。
最后，我们要有循环退出的情况。在找到有效路径之后，当前节点等于终点，这样就能够退出循环了。

until currentNode == endNode //end main do...until loop

如果在成功的情况下退出do…until 循环，我们会得到一条链表通过parent 从终点指向起点。由于我们想要得到从起点到终点的路径，所以必须将其反转。有很多种方法反转链表，最简单的方法就是使用栈。
下图显示了贪婪最佳优先算法作用在示例数据集的开始两次迭代。在(a) 中，起点加入封闭集合，而邻接节点则加入开放集合。每个邻接节点（蓝色）都有用曼哈顿距离算出来的自己到达终点的ℎ(x) 开销。箭头表示子节点指向父节点。这个算法的下一步就是选择最低ℎ(x) 值节点，在这里会选择ℎ = 3 的节点。然后这个节点就会作为当前节点，放到封闭集合里。(b) 显示了下一步的迭代，将当前节点（黄色）的邻接节点放入开放集合中。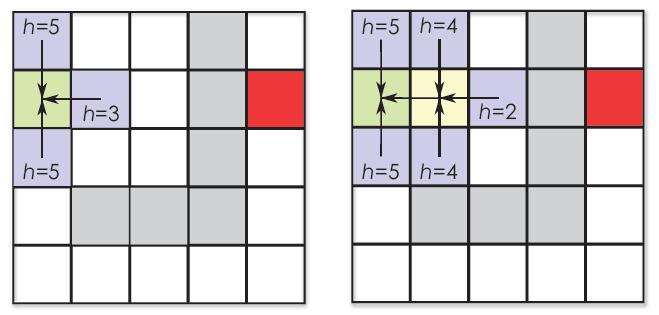

在目标节点（红色）加到封闭集合之后，我们会得到从终点到起点的链表。这个链表可以通过反转得到之前贪婪最佳优先路径。
完整的贪婪最佳优先算法如下。注意这个实现假设ℎ(x) 的值在执行过程中总是不变的。

curentNode = startNode
add currentNode to closedSet
do
    // 把邻接节点加入开放集合
    foreach Node n adjacent to currentNode
        if closedSet contains n
            continue
        else
            n.parent = currentNode
            if openSet does not contain n
                compute n.h
                add n to openSet
            end
        end
    loop
         // 所有可能性都尝试过了
        if openSet is empty
            break
        end
        // 选择新的当前节点
        currentNode = Node with lowest h in openSet
        remove currentNode from openSet
        add currentNode to closedSet
    until currentNode == endNode
    // 如果路径解出， 通过栈重新构造路径
    if currentNode == endNode
        Stack path
        Node n = endNode
        while n is not null
            push n onto path
            n = n.parent
        loop
else
    // 寻路失败
end

如果我们不想用栈构造路径，另一个方案就是直接计算起点到终点的路径。这样，在寻路结束的时候就能得到从起点到终点的路径，可以节省一点计算开销。

本文选自《游戏编程算法与技巧》一书。

想及时获得更多精彩文章，可在微信中搜索“博文视点”或者扫描下方二维码并关注。