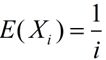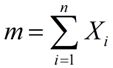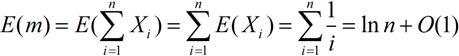概率分析和随机算法(1)——算法导论(5)

1. 雇用问题

(1) 提出问题

    你的老板让你为公司雇用一名程序员，现在有n个人投了简历。你每天会随机的从这n份简历中挑选一份，然后让对应的投简历者过来面试，每次面试都将花费C1。而你的雇用原则是：如果当前面试的程序员比目前的程序员优秀，那么你就辞掉目前的程序员，而花高价C2去聘请面试的这位程序员。你的老板愿意为该策略付费，但是想让你估算一下该费用会是多少。

下面是这种策略的伪代码：

 

 

 

 

 

 

 

(2) 不科学的算法

    因为不管最优秀的面试者出现在哪一个位置，我们总是要面试完所有人，因此面试的费用是固定的，为C1*n；假设在这n次面试中，需要雇佣m个人，那么你将花费C2 * m雇佣费。因此总费用w为：  w = C1*n +  C2 * m。

   你可能认为最好的情况是：最优秀的面试者出现在第一位，m=1；最坏的情况是：最优秀的面试者出现在最后一位，m=n。因此平均情况是，m = (n+1)/ 2。这种简单的由上下限取平均的做法在这里是不科学的，因为总费用m的分布并不是均匀的（从下面可以看出）。

2. 概率分析

我们考虑平均要雇用的人数m。设随机变量Xi表示第i名面试的人是否被雇用（若被雇佣Xi为1，否则为0）。

那么因此m的期望E(m) 为：

 

因此平均将花费：w = C1*n + C2 * E(m) = O(ln n)，这比最坏情况下的雇用费用O(n)有了很大的改进。

3. 随机算法

   

    在上面，我们通过对m的分布分析出平均情况，但是在很多时候，我们是无法得知输入分布信息的。但我们也许可以设计一个随机算法。

    针对上面的雇用问题，我们可以在算法运行前先随机地排列应聘者，以加强所有的排列都是等可能出现的。

    下面是随机算法的伪代码描述：

    

    现在我们关心的重点在于如何生成一个随机的排列。不失一般性，我们假定一个数组A，包含1~n 这n个元素，我们的目标是构造出数组A的随机数组。下面介绍两种算法：

    方法① ：我们先构造一个长度为n的数组P，数组P中的元素是介于1到n³的随机数。然后我们把数组P中的元素作为数组A中对应位置元素的优先级，数组A中的元素按照优先级大小进行排列（优先级相等的随便排列）。例如，A={1, 2, 3, 4}, P = {13,1, 60, 28}（数组P说明 数组A中，1的优先级是13，2的优先级是1，…），那么排列后的A={2，1，4，3}（按优先级从小到大排列）。伪代码如下：

至于排序算法，举不胜数，以后会专门讨论。

证明略（有兴趣的可以自己去看原书）。

    方法②：比较简单，直接贴出伪代码：

证明略。

下面给出这两种随机数组的生成算法的Java实现代码：

public static void main(String[] args) {
	printArray(permuteBySort(10));
	printArray(randomizeInPlace(10));
}

/**
 * 生成随机数组（方法1）
 * 
 * @param length
 *            数组规模
 * @return
 */
private static int[] permuteBySort(int length) {
	int[] a = new int[length];
	for (int i = 0; i < length; i++) {
		a[i] = i + 1;
	}
	Random random = new Random(System.currentTimeMillis());
	int[] p = new int[length];
	for (int i = 0; i < p.length; i++) {
		// 注意这里强制类型转换很可能会丢失数据
		p[i] = random.nextInt((int) Math.pow(length, 3)) + 1;
	}
	// 冒泡排序法
	for (int i = 0; i < p.length; i++) {
		for (int j = 0; j < p.length - 1 - i; j++) {
			if (p[j] > p[j + 1]) {
				int temp = p[j];
				p[j] = p[j + 1];
				p[j + 1] = temp;
				temp = a[j];
				a[j] = a[j + 1];
				a[j + 1] = temp;
			}
		}
	}
	return a;
}

/**
 * 生成随机数组（方法2）
 * 
 * @param length
 *            数组规模
 * @return
 */
private static int[] randomizeInPlace(int length) {
	int[] a = new int[length];
	for (int i = 0; i < length; i++) {
		a[i] = i + 1;
	}
	Random random = new Random(System.currentTimeMillis());
	for (int i = 0; i < a.length; i++) {
		int swapIndex = random.nextInt(a.length - i) + i;
		int temp = a[i];
		a[i] = a[swapIndex];
		a[swapIndex] = temp;
	}
	return a;
}

/**
 * 打印数组
 * 
 * @param a
 */
private static void printArray(int[] a) {
	for (int i : a) {
		System.out.print(i + "");
	}
	System.out.println();
}

 

 

 

ps：以上内容均摘自《算法导论》中文译本。本人只是提取出文中个人认为比较重要的点，加入了一些个人理解，仅供参考。

转载于:https://www.cnblogs.com/dongkuo/p/4807953.html