2019牛客暑期多校训练营（第七场） E (线段树, 点代表一个区间)

 

给你的区间 是 1e9 的,所以需要我们离散一下,然后每个点代表一个区间就可以了. 

思路:

首先我们考虑到 N 是4e5 的,所以说不同点的个数最多就是 2*N 的,

我们就可以用线段树来做 了.

方法一:

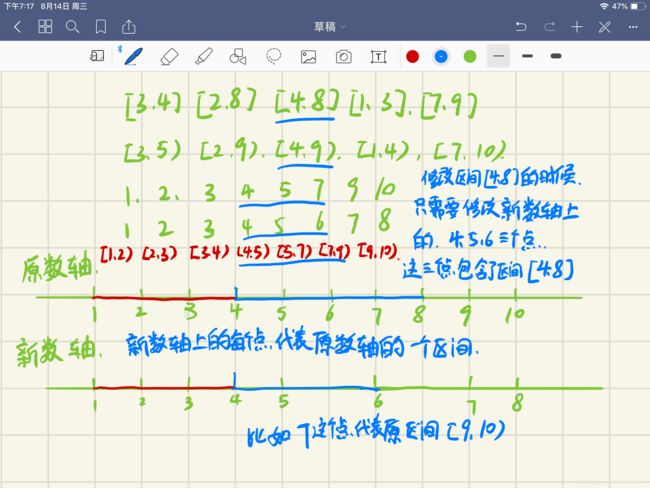
我们考虑离散一个区间,把 右区间的端点 +1,区间算是左闭右开的, 这样算一个区间的值就是 右端点的值减去左区间的值.

我们就可以用 左区间的值代表整个区间.

[1,7] [5,10]
我们换成左闭右开的区间 .
[1,8 )  [5,11).
然后离散化 .
1 5 8 11

每个点代表的区间就是 [ a[i], a[i+1] )

1 这个点代表区间 [1,5) .
2 这个点代表区间 [5,8) .
3 这个点代表区间 [8,11).
4 这个点代表 最右面的端点.
区间变成了.
[1,3)  [2,4)

a[3] - a[1] 就是第一个区间的值.
a[4] - a[2] 就是第二个区间的值.

当我们处理第一区间的时候,
只需要修改  [1,2] 这个区间就可以了,它代表原来的 [1,7] 这个区间,
处理第二个区间的时候,
只需要修改 [2,3] 这个区间就是了,代表原来的 [5,10] 这个区间.

加了一个样例的解释.

 

 

最后查询的时候,我们要找到具体的点,然后由点去找具体的区间.
由点去找对应的区间就很好找.随便搞搞就行了. 

方法二:
我们可以不换成左闭右开的区间,
然后我们有 2*N 个点,这些点就代表一个点,然后每两个相邻的点之间我们在加一个点,代表两个点相邻的区间.

[1,7] [5,10]
我们离散化之后
1 5 7 10
每个点代表的区间就是.
[1,1] [2,4], [5,5] ,[6,6],[7,7],[8.9] ,[10,10]
要修改 [1,7] 这个区间,我们就需要修改 [1,5] 这个区间,
要修改 [5,10] 就要修改,[3,7] 这个区间.

方法一的代码:

#include
#define ls now << 1
#define rs now << 1 | 1
using namespace std;
const int N  = 4e5 + 100;
const int M = N << 2;
long long x[N], y[N],z[M];

namespace SEG {
    long long val[M<<2], lz[M<<2];
    void pushdown(int now, int l, int r){
        if (lz[now] == 0) return;
        int mid = (l + r) >> 1;
        val[ls] += (z[mid] - z[l])*lz[now];
        val[rs] += (z[r] - z[mid])*lz[now];
        lz[ls] += lz[now]; lz[rs] += lz[now];
        lz[now] = 0;
    }
    void Modify(int now, int l, int r, int a, int b){
        if (a <= l && b >= r - 1){
            lz[now] += 1;
            val[now] += z[r] - z[l]; 
            return;
        }
        pushdown(now,l,r);
        int mid = (l + r) >> 1;
        if (a < mid) Modify(ls, l, mid, a, b);
        if (b >= mid) Modify(rs, mid,r,a,b);
        val[now] = val[ls] + val[rs];
    }
    int Query(int now, int l, int r, long long k){
        if (l + 1 == r){
            long long tmp = val[now] / (z[r] - z[l]);
            k = (k - 1) / tmp;
            return z[l] + k;
        }
        pushdown(now, l, r);
        int mid = (l + r) >> 1;
        if (k <= val[ls]) return Query(ls, l, mid, k);
        if (k > val[ls]) return Query(rs, mid, r, k - val[ls]);
        return 0;
    }

};
long long a1, a2, b1, b2, c1, c2, m1, m2;
int   n, m, tot,l[N],r[N],cnt;
int main() {
    scanf("%d",&n);
    scanf("%lld%lld%lld%lld%lld%lld", &x[1], &x[2], &a1, &b1, &c1, &m1);
    scanf("%lld%lld%lld%lld%lld%lld", &y[1], &y[2], &a2, &b2, &c2, &m2);
    for (int i = 3; i <= n; ++i) {
        x[i] = ((a1 * x[i - 1]) + (1ll*b1 * x[i - 2]) + c1) % m1;
        y[i] = ((a2 * y[i - 1]) + (1ll*b2 * y[i - 2]) + c2) % m2;
    }

    for (int i = 1; i <= n; ++i) {
        l[i] = min(x[i], y[i]) + 1;
        r[i] = max(x[i], y[i]) + 1 + 1;
        z[++tot] = l[i];
        z[++tot] = r[i];
    }
    sort(z+1, z + tot+1);
    tot = unique(z+1, z + tot + 1) - z - 1;
    for (int i = 1; i <= n; ++i) {
        l[i] = lower_bound(z+1,z+tot+1,l[i]) - z;
        r[i] = lower_bound(z+1,z+tot+1,r[i]) - z;
    }
    long long tmp = 0;
    for (int i = 1; i <= n; ++i){
        SEG::Modify(1,1,tot+1,l[i],r[i] - 1);
        tmp += z[r[i]] - z[l[i]];
        int ans =  SEG::Query(1,1,tot+1,(tmp + 1) / 2);
        printf("%d\n",ans);
    }
    return 0;
}
/*
5
3 1 4 1 5 9
2 7 1 8 2 9
5
1 2 3 4 5 4
2 3 4 5 6 4


*/

方法二的代码:

#include
#define ls now << 1
#define rs now << 1 | 1
using namespace std;
const int N  = 4e5 + 100;
const int M = N << 2;
int x[M], y[M];

namespace SEG {
    long long val[M << 2];
    int lz[M << 2];
    void pushdown(int now, int l, int r) {
        if (lz[now] == 0) return;
        int mid = (l + r) >> 1;
        val[ls] += 1ll * (y[mid] - x[l] + 1) * lz[now];
        val[rs] += 1ll * (y[r] - x[mid + 1] + 1) * lz[now];
        lz[ls] += lz[now];
        lz[rs] += lz[now];
        lz[now] = 0;
    }
    void Modify(int now, int l, int r, int a, int b) {
        if (l > r) return;
        if (a <= l && b >= r) {
            lz[now] += 1;
            val[now] += y[r] - x[l] + 1;
            return;
        }
        pushdown(now, l, r);
        int mid = (l + r) >> 1;
        if (a <= mid) Modify(ls, l, mid, a, b);
        if (b > mid) Modify(rs, mid + 1, r, a, b);
        val[now] = val[ls] + val[rs];
    }
    int Query(int now, int l, int r, long long k) {
        if(l > r) return 0;
        if (l == r) {
            long long tmp = val[now] / (y[l] - x[l] + 1);
            k = (k - 1) / tmp;
            return x[l] + k;
        }
        pushdown(now, l, r);
        int mid = (l + r) >> 1;
        if (k <= val[ls]) return Query(ls, l, mid, k);
        if (k > val[ls]) return Query(rs, mid + 1, r, k - val[ls]);
        return 0;
    }

};
int a1, a2, b1, b2, c1, c2, m1, m2;
int  z[M], n, m, tot, l[N], r[N], cnt;
int main() {
    scanf("%d", &n);
    scanf("%d%d%d%d%d%d", &x[1], &x[2], &a1, &b1, &c1, &m1);
    scanf("%d%d%d%d%d%d", &y[1], &y[2], &a2, &b2, &c2, &m2);
    for (int i = 3; i <= n; ++i) {
        x[i] = ((1ll * a1 * x[i - 1]) % m1 + (1ll * b1 * x[i - 2]) % m1 + c1) % m1;
        y[i] = ((1ll * a2 * y[i - 1]) % m2 + (1ll * b2 * y[i - 2]) % m2 + c2) % m2;
    }

    for (int i = 1; i <= n; ++i) {
        l[i] = min(x[i], y[i]) + 1;
        r[i] = max(x[i], y[i]) + 1;
        z[tot++] = l[i];
        z[tot++] = r[i];
    }

    sort(z, z + tot);
    tot = unique(z, z + tot) - z;
    for (int i = 0; i < tot; ++i) {
        if (i) {
            if (z[i - 1] + 1 < z[i]) {
                x[++cnt] = z[i - 1] + 1;
                y[cnt] = z[i] - 1;
            }
        }
        x[++cnt] = z[i], y[cnt] = z[i];
    }
    for (int i = 1; i <= n; ++i) {
        l[i] = lower_bound(x + 1, x + cnt + 1, l[i]) - x;
        r[i] = lower_bound(y + 1, y + cnt + 1, r[i]) - y;
    }
    long long tmp = 0;
    for (int i = 1; i <= n; ++i) {
        SEG::Modify(1, 1, cnt, l[i], r[i]);
        tmp = tmp + (y[r[i]] - x[l[i]] + 1);
        int ans =  SEG::Query(1, 1, cnt, (tmp + 1) / 2);
        printf("%d\n", ans);
    }
    return 0;
}
/*
5
3 1 4 1 5 9
2 7 1 8 2 9
5
1 2 3 4 5 4
2 3 4 5 6 4


*/