线性回归--PM2.5预测--李宏毅机器学习

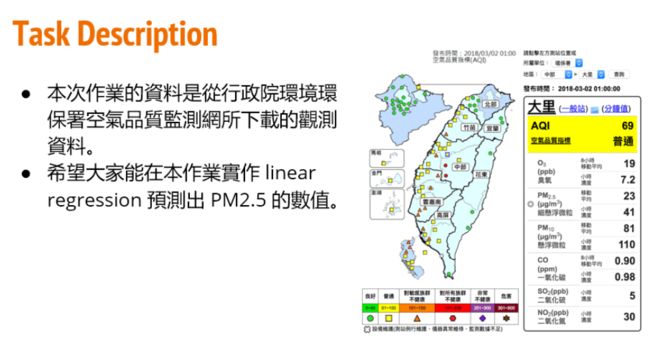
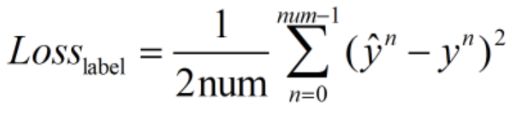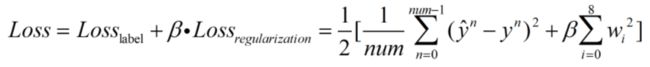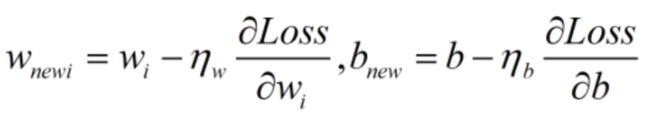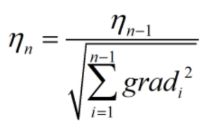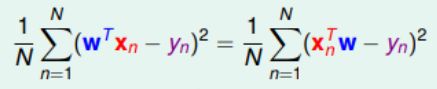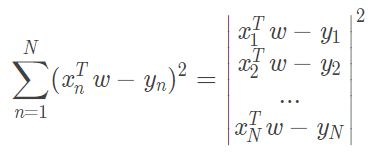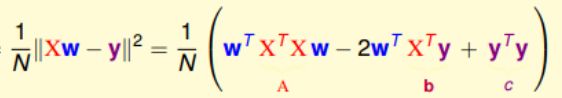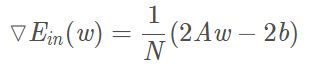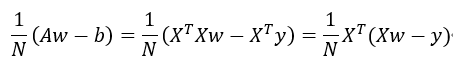一、说明

给定训练集train.csv，要求根据前9个小时的空气监测情况预测第10个小时的PM2.5含量。

训练集介绍：

　　(1)、CSV文件，包含台湾丰原地区240天的气象观测资料(取每个月前20天的数据做训练集，12月X20天=240天，每月后10天数据用于测试，对学生不可见);

　　(2)、每天的监测时间点为0时，1时......到23时，共24个时间节点;

　　(3)、每天的检测指标包括CO、NO、PM2.5、PM10等气体浓度，是否降雨、刮风等气象信息，共计18项；

二、数据处理

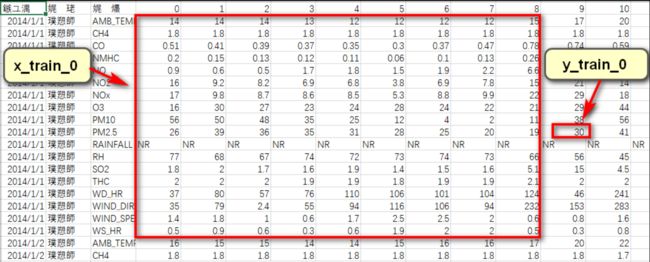
根据要求，要用前9个小时的数据，来预测第10个小时的PM2.5值。一笔训练数据如下图所示：

数据中存在一定量的空数据NR，且多存在于RAINFALL一项。对于空数据，常规的处理方法无非就是删除法和补全法两种。

RAINFALL表示当天对应时间点是否降雨，因此可以采用补全法处理空数据：将空数据NR全部补为0即可。

# 将NR替换成 0
data = data.replace(['NR'], [0.0])

 我们先将数据进行预处理，得到 每笔训练数据 和对应的 结果label。

 

1. 由于每个月前20天的数据检测是连续24小时进行的，所以为了得到多笔数据，先将每个月20天数据 “连起来”，如下图示：

               

每个月的数据就是18行480(24*20)列,一共12个月的数据。

# 将每个月20天数据连成一大行
    month_data = []
    for month in range(12):
        # 每个月的数据
        sub_data = np.empty([18, 20*24])
        for day in range(20):
            # 每一天的数据
            sub_data[:, day*24:(day+1)*24] = data[(month*18*20+day*18):(month*18*20+(day+1)*18), :]
        month_data.append(sub_data)

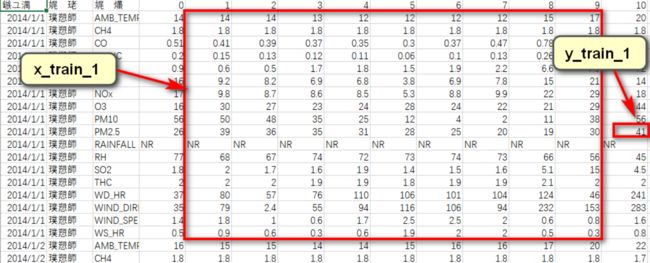
2. 对于连续的10个小时，可以取一笔 9小时训练数据（输入） 和 第10小时对应PM2.5值（结果）。

每个月20天，20*24=480小时， 480-9=471，每个月可以取471笔数据。   

       

# 将每个月中20天，相邻9个小时生成一笔数据，第10个小时的pm2.5值，生成一个label
    for i in range(12):
        sub_data = month_data[i]
        for j in range(20*24-9):
            # 相邻9小时的数据
            x_list.append(sub_data[:, j:j+9])
            # 第10小时的 pm2.5
            y_list.append(sub_data[9, j+9])

完整数据处理代码：

def data_process(data):
    x_list , y_list = [], []
    # 将NR替换成 0
    data = data.replace(['NR'], [0.0])
    # astype() 转换为float
    data = np.array(data).astype(float)
    # 将每个月20天数据连成一大行
    month_data = []
    for month in range(12):
        # 每个月的数据
        sub_data = np.empty([18, 20*24])
        for day in range(20):
            # 每一天的数据
            sub_data[:, day*24:(day+1)*24] = data[(month*18*20+day*18):(month*18*20+(day+1)*18), :]
        month_data.append(sub_data)

    # 将每个月中20天，相邻9个小时生成一笔数据，第10个小时的pm2.5值，生成一个label
    for i in range(12):
        sub_data = month_data[i]
        for j in range(20*24-9):
            # 相邻9小时的数据
            x_list.append(sub_data[:, j:j+9])
            # 第10小时的 pm2.5
            y_list.append(sub_data[9, j+9])

    x = np.array(x_list)
    y = np.array(y_list)

    return x, y, month_data

View Code

二、模型建立

如题所说，使用的是最简单的线性回归模型，作为课程作业没有那么难,但也从中学到不少东西。

 

2.1 线性回归模型

       

 如果把b作为w0，加到权值向量前面，可以得到向量运算的形式，如下：

    h(X) = W^TX        #  W为权值， X为输入。

 

2.2 损失函数

用预测值与label之间的平均欧式距离来衡量预测的准确程度，并充当损失函数。

这里的损失指的是平均损失；乘1/2是为了在后续求梯度过程中保证梯度项系数为1，方便计算。

 为了防止过拟合，加入正则项：

 完整的损失函数：

 

2.3 梯度下降

对参数 w 和 b 求偏导：

 对参数进行更新：

   η_w、η_b 为学习率。

 

2.4 学习率更新

为了在不影响模型效果的前提下提高学习速度，可以对学习率进行实时更新：即让学习率的值在学习初期较大，之后逐渐减小。

这里采用比较经典的adagrad算法来更新学习率：

      根号下为梯度的累加值。

 

2.5 矩阵加速计算推导

因为python中使用矩阵的计算速度非常快，远远快于循环计算，所以这里我们推导一下利用矩阵计算梯度值的写法。

具体可以参照这篇博客：https://blog.csdn.net/sjz_hahalala479/article/details/81701164

 

前文提到过，如果把b作为w0，加到权值向量前面可以得到如下形式：

    h(X) = W^TX        #  W为权值， X为输入。  W = [b, w0, w1, ...]

 

对于损失函数的转化改造：

^_对于 

 

 1. 将平方求和改造成向量模的平方： 

 

^{假设我们有个向量} 

^所以有

 

 

 

 ^{将平方项展开：}        

对W进行求偏导：              ^{与上面展开对应}

所以我们要求的梯度就是：   

 

 *这里将分子的2去掉是因为与的损失函数分母抵消。

# 计算梯度 W = X转置.(XW-Y)
w_1 = np.dot(X.transpose(), X.dot(W)-y_train)

三、训练模型

3.0 数据转化

将训练数据分成两部分（8：2），一部分用来训练，一部分用来验证效果。

# 8:2 cross validation
    x_train = x[:(int)(x.shape[0]*0.8)]
    y_train = y[:(int)(x.shape[0]*0.8)]
    x_val = x[(int)(x.shape[0]*0.8+0.5):]
    y_val = y[(int)(y.shape[0]*0.8+0.5):]

由于参数太多，也可以取其中的几类进行训练，比如下文中将选取NO、NO2、NO_x、O3、PM10、PM2.5作为输入。

其中的一笔数据如下：

 首先将每笔数据的输入转化成一行，并在前面加上 1， 对应于bias项。

# 定义参数 b，w   b作为w0
W = np.ones(1+9*6)
# 将训练数据转化成 每一笔数据一行，并且前面添加 1，作为b的权值 [[1, ...], [1, ...],...,[1, ...]]
X = np.empty([n, W.size-1])
for i in range(n):
    X[i] = x_train[i][4:10].reshape(1, -1)
# 添加 1
X = np.concatenate((np.ones([n, 1]), X), axis=1)

3.1 训练函数

完整的训练函数代码如下，具体请看注释：

def train(x_train, y_train, times):
    # 定义参数 b，w   b作为w0
    W = np.ones(1+9*6)
    # 多少笔数据
    n = y_train.size
    # 学习率
    learning_rate = 100
    # 正则项大小
    reg_rate = 0.011

    # 将训练数据转化成 每一笔数据一行，并且前面添加 1，作为b的权值 [[1, ...], [1, ...],...,[1, ...]]
    X = np.empty([n, W.size-1])
    for i in range(n):
        X[i] = x_train[i][4:10].reshape(1, -1)
    # 添加 1
    X = np.concatenate((np.ones([n, 1]), X), axis=1)

    # 累加正则项
    adagrad=0
    # 正则项的选择矩阵， 去掉bias部分
    reg_mat=np.concatenate((np.array([0]), np.ones([9*6,])), axis=0)

    for t in range(times):
        # 计算梯度 W = X转置.(XW-Y)
        w_1 = np.dot(X.transpose(), X.dot(W)-y_train)
        # 加正则项
        w_1 += reg_rate * W * reg_mat
        # 正则项参数更新
        adagrad += sum(w_1**2)**0.5
        # 梯度下降
        W -= learning_rate/adagrad * w_1
        # 每200次迭代输出一次
        if t%200==0:
            loss = 0
            for j in range(n):
                loss += (y_train[j]-X[j].dot(W))**2
            print(t)
            print('times ', loss/n)

    return W

3.2 验证

def validate(x_val, y_val, w):
    n=y_val.size
    # 转化成一行，并加一列 1
    X = np.empty([n, w.size - 1])
    for i in range(n):
        X[i] = x_val[i][4:10].reshape(1, -1)
    X = np.concatenate((np.ones([n, 1]), X), axis=1)

    loss=0
    # 计算loss
    for j in range(n):
        loss += (y_val[j] - X[j].dot(W)) ** 2

    return loss/n

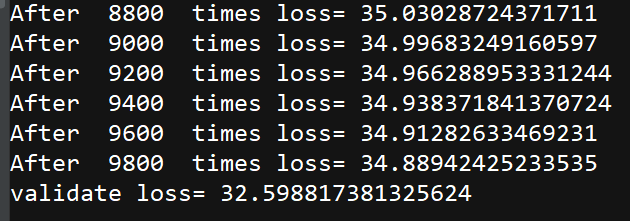
四、结果分析

运行输出的结果看，loss还是挺大的，还有改进的空间。

 

 改进思路：

1. 分割训练集和验证集时，应该按照比例随机抽取数据帧作为训练集和验证集，选取loss最小的模型。

2. 充分考虑其他参数对空气PM2.5的影响，加入更加复杂的高次项。

五、预测结果

对test集的数据进行结果预测

## 计算预测值  ##
    Y = X_test.dot(W)
    # 预测值写入
    data_test = np.array(data_test)
    data_test = np.concatenate((data_test, np.zeros([n, 1])), axis=1)
    for j in range(0, n, 18):
        data_test[j+9, 11] = int(Y[int(j/18)]+0.5)

为了方便查看，将数据写回源文件格式。

# 保存结果
    data_test = pd.DataFrame(data_test)
    data_test.to_csv('test_res.csv')

第一笔数据的预测值：

 

 六、程序代码

**在项目根目录存放‘train.csv’、'test.csv'

**每次训练后会保存参数，下次训练时请事先删除根目录文件‘weight_2.npy’

import pandas as pd
import numpy as np

def data_process(data):
    x_list , y_list = [], []
    # 将NR替换成 0
    data = data.replace(['NR'], [0.0])
    # astype() 转换为float
    data = np.array(data).astype(float)
    # 将每个月20天数据连成一大行
    month_data = []
    for month in range(12):
        # 每个月的数据
        sub_data = np.empty([18, 20*24])
        for day in range(20):
            # 每一天的数据
            sub_data[:, day*24:(day+1)*24] = data[(month*18*20+day*18):(month*18*20+(day+1)*18), :]
        month_data.append(sub_data)

    # 将每个月中20天，相邻9个小时生成一笔数据，第10个小时的pm2.5值，生成一个label
    for i in range(12):
        sub_data = month_data[i]
        for j in range(20*24-9):
            # 相邻9小时的数据
            x_list.append(sub_data[:, j:j+9])
            # 第10小时的 pm2.5
            y_list.append(sub_data[9, j+9])

    x = np.array(x_list)
    y = np.array(y_list)

    return x, y, month_data

def train(x_train, y_train, times):
    # 定义参数 b，w   b作为w0
    W = np.ones(1+9*6)
    # 多少笔数据
    n = y_train.size
    # 学习率
    learning_rate = 100
    # 正则项大小
    reg_rate = 0.011

    # 将训练数据转化成 每一笔数据一行，并且前面添加 1，作为b的权值 [[1, ...], [1, ...],...,[1, ...]]
    X = np.empty([n, W.size-1])
    for i in range(n):
        X[i] = x_train[i][4:10].reshape(1, -1)
    # 添加 1
    X = np.concatenate((np.ones([n, 1]), X), axis=1)
    # data_X = pd.DataFrame(X)
    # data_X.to_csv('data.csv')
    adagrad=0
    # 正则项的选择矩阵， 去掉bias部分
    reg_mat=np.concatenate((np.array([0]), np.ones([9*6,])), axis=0)

    for t in range(times):
        # 计算梯度 W = X转置.(XW-Y)
        w_1 = np.dot(X.transpose(), X.dot(W)-y_train)
        # 加正则项
        w_1 += reg_rate * W * reg_mat
        # 正则项参数更新
        adagrad += sum(w_1**2)**0.5
        # 梯度下降
        W -= learning_rate/adagrad * w_1
        # 每200次迭代输出一次
        if t%200==0:
            loss = 0
            for j in range(n):
                loss += (y_train[j]-X[j].dot(W))**2
            print('After ', t,' times loss=', loss/n)

    return W

def validate(x_val, y_val, w):
    n=y_val.size
    # 转化成一行，并加一列 1
    X = np.empty([n, w.size - 1])
    for i in range(n):
        X[i] = x_val[i][4:10].reshape(1, -1)
    X = np.concatenate((np.ones([n, 1]), X), axis=1)

    loss=0
    # 计算loss
    for j in range(n):
        loss += (y_val[j] - X[j].dot(W)) ** 2
    return loss/n

if __name__ == '__main__':

    data = pd.read_csv('./train.csv', encoding='big5')
    # 去掉前三列
    data = data.iloc[:, 3:]
    [x, y, month_data] = data_process(data)

    # 8:2 cross validation
    x_train = x[:(int)(x.shape[0]*0.8)]
    y_train = y[:(int)(x.shape[0]*0.8)]
    x_val = x[(int)(x.shape[0]*0.8+0.5):]
    y_val = y[(int)(y.shape[0]*0.8+0.5):]

    try:
        W = np.load('weight_2.npy')
    except:
        # 迭代次数
        times = 10000
        W = train(x_train, y_train, times)
        np.save('weight_2.npy', W)

    ## 计算在val上的loss  ##
    loss = validate(x_val, y_val, W)
    print('validate loss=', loss)

    ## 在test上进行验证  ##
    # header=None 无表头读入
    data_test = pd.read_csv('./test.csv', header=None, encoding='big5')
    # 去掉前两列
    test = data_test.iloc[:, 2:]
    test = test.replace(['NR'], [0.0])
    #处理数据
    test = np.array(test).astype(float)
    [n, m] = test.shape
    # 读出参数值
    X_test = np.empty([int(n/18), 9*6])
    for i in range(0, n, 18):
        X_test[int(i/18), :] = test[i+4:i+10, :].reshape(1, -1)

    [n_test, m_test] = X_test.shape
    # 加一列 1
    X_test = np.concatenate((np.ones([n_test, 1]), X_test), axis=1)

    ## 计算预测值  ##
    Y = X_test.dot(W)
    # 预测值写入
    data_test = np.array(data_test)
    data_test = np.concatenate((data_test, np.zeros([n, 1])), axis=1)
    for j in range(0, n, 18):
        data_test[j+9, 11] = int(Y[int(j/18)]+0.5)

    # 保存结果
    data_test = pd.DataFrame(data_test)
    data_test.to_csv('test_res.csv')

View Code

 

感谢阅读，如有错误欢迎留言指正。

如果感觉对你有所帮助，↘右下推荐点一点。

 

ps：本文实现参照以下两篇博客：

https://www.cnblogs.com/HL-space/p/10676637.html    

https://mrsuncodes.github.io/2020/03/15/%E6%9D%8E%E5%AE%8F%E6%AF%85%E6%9C%BA%E5%99%A8%E5%AD%A6%E4%B9%A0-%E7%AC%AC%E4%B8%80%E8%AF%BE%E4%BD%9C%E4%B8%9A/