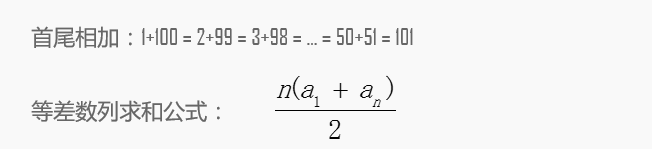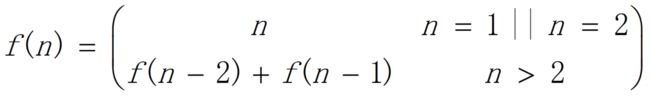简单递归入门题

一、猴子吃桃问题

孙悟空第一天摘下若干蟠桃，当即吃了一半，还不过瘾，又多吃了一个。第二天早上，他又将剩下的蟠桃吃掉一半，还不过瘾，又多吃了一个。之后每天早上他都吃掉前一天剩下桃子的一半零一个。到第10天早上想再吃时，就只剩下一个蟠桃了。求孙悟空第一天共摘了多少个蟠桃？
分析：

1.猴子吃桃问题的递推算法

/**
 * 递推算法
 */
public int eat01(int n){
    int a=1;
    //也可以这样考虑,“第1天开始吃桃子，连续吃了n-1天”
    //写成for(int i=1;i<=n-1;i++)，无所谓，结果一样
    for(int i=2;i<=n;i++){
        a=2*a+2;
    }
    return a;
}

2. 猴子吃桃问题的递归算法

/**
 * 递归算法
 */
public int eat02(int n){
    System.out.println("f("+n+")压栈");
    if(n==1){
        System.out.println("此时函数栈达到最大深度!");
        System.out.println("f("+n+")弹栈");
        return 1;
    }else{
        int a=eat02(n-1)*2+2;
        System.out.println("f("+n+")弹栈");
        return a;
    }
}

---

/**
 * 递归算法
 * 用三元运算符把代码简化为一行
 */
public int eat03(int n){
    return n==1?1:eat03(n-1)*2+2;
}

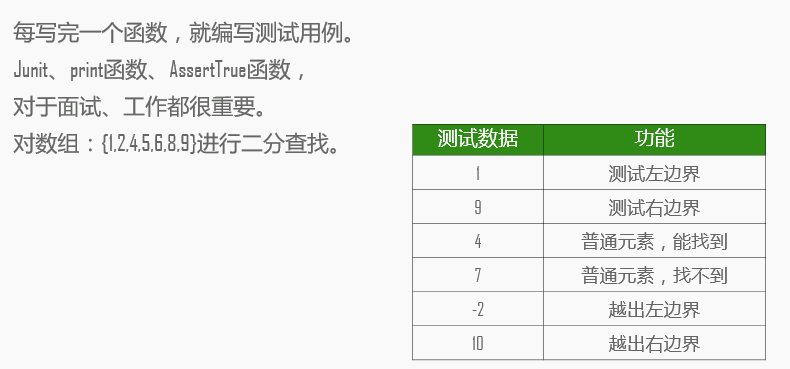
3.断言：AssertTrue

/**
 * 模拟猴子吃桃的过程
 * 用断言验证正确性
 */
public void check(int n,int num){
    int a=num;
    for(int i=2;i<=n;i++){
        a=a/2-1;
    }
    System.out.println(a);
    Assert.assertTrue(a==1);
}
@Test
public void test01(){
    int n=10;
    int num=eat01(n);
    System.out.println(num);
}
@Test
public void test02(){
    int n=10;
    int num=eat02(n);
    System.out.println(num);
}
@Test
public void test03(){
    //当n很大的时候，函数栈会溢出
    int n=12000;
    int num=eat03(n);
    System.out.println(num);
}
@Test
public void testCheck(){
    int n=10;
    int num=1534;
    check(n, num);
}
}

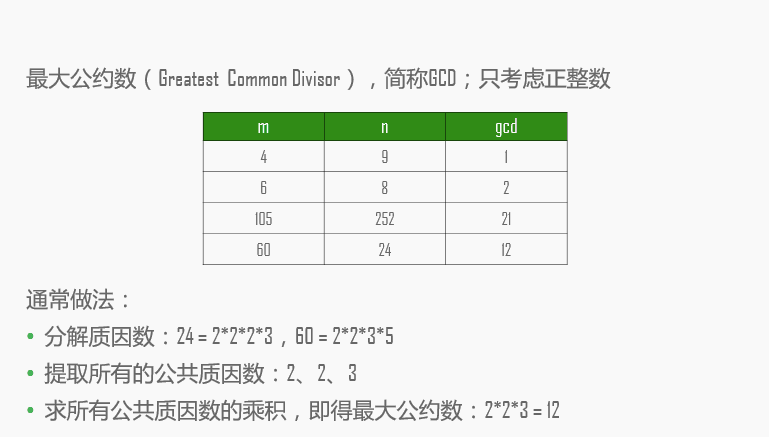
二、最大公约数与最小公倍数

1.辗转相除法的思想

古希腊数学家欧几里得（公元前330年—公元前275年）发明了一种巧妙的算法——辗转相除法，又称欧几里得算法：
令较大数为m，较小数为n；
当m除以n的余数不等于0时，把n作为m，并把余数作为n，进行下一次循环；
当余数等于0时，返回n

2.最大公约数的非递归算法

/**
 * 最大公约数的递推算法
 */
public int gcd01(int m,int n){
    int a=Math.max(m, n);
    int b=Math.min(m, n);
    m=a;
    n=b;
    int r;
    while(m%n!=0){
        r=m%n;
        m=n;
        n=r;
    }
    return n;
}

3.最大公约数的递归算法

/**
 * 最大公约数的递归算法
 */

public int gcd02(int m,int n){
    /*int a=Math.max(m, n);
    int b=Math.min(m, n);
    if(a%b==0){
        return b;
    }else{
        return gcd02(b, a%b);
    }*/
    return m>=n?m%n==0?n:gcd02(n, m%n):n%m==0?m:gcd02(m, n%m);
}  

分析：

每执行一次循环，m或者n至少有一个缩小了2倍，故时间复杂度上限为log2M。
对于大量的随机测试样例，每次循环平均能使m与n的值缩小一个10进位，所以平均复杂度为O(lgM)。

4.最小公倍数的求法

求出最大公约数之后，最小公倍数（Least Common Multiple，简称LCM），就能迎刃而解了。
LCM(m,n) = m*n/GCD(m,n)
比如，60与24的最大公约数为12，那么最小公倍数为：60×24/12 = 120。

public int lcm(int m,int n){
    return m*n/gcd01(m, n);
}

---

三、1到100累加的“非主流算法”

**题目：求1+2+3+…+n
用递归以及非递归算法求解，要求时间复杂度为O(N)**

1.普通算法

/**
 *递推算法
 */
public int commonMethod01(int n){
    int sum=0;
    for(int i=1;i<=n;i++){
        sum+=i;
    }
/**
 * 递归算法
 */
public int commonMethod02(int n){
    if(n==1){
        return 1;
    }else{
        return commonMethod02(n-1)+n;
    }
}

2.等差数列求和公式

public int commonMethod03(int n){
    return n*(1+n)/2;
}

3.如何终止？抛异常！

如果加上以下限制，该如何求解？
* 不允许使用循环语句(不能递推)
* 不允许使用选择语句（不能递归）
* 不允许使用乘法、除法（不能用求和公式）
**如果不能人为地终止循环或者递归，那就让程序意外终止。
自然而然就联想到：抛异常！**

代码示例：

public class Diguitest {
private int n;
private int [] array;

public Diguitest(int n) {
        super();
        this.n=n;
        array=new int[n+1];
    }

    public int sumMethod(int i){
        try {       
            array[i]=array[i-1]+i;
            int k=sumMethod(i+1);
            return k;
//这里是向上递归，array[1]=array[0]+1 然后array【2】=array【1】+2
//array[3]=array[2]+3、、、一直到内存数组爆了然后输出array【n】
//n次递归，时间复杂度为O(n),创建了n个数组空间，空间复杂度为O(n).
//堆内存和栈内存都为n
        } catch (ArrayIndexOutOfBoundsException e) {
            return array[n];
        }
    }

}
//测试代码：
    @org.junit.Test
    public void test() {
    Diguitest diguitest=new Diguitest(100);
    int sum=diguitest.sumMethod(1);
    System.out.println(sum);
        }

四、爬楼梯问题

leetCode70：Climbing Stairs
楼梯一共有n级，每次你只能爬1级或者2级。
问：从底部爬到顶部一共有多少种不同的路径？

斐波那契数列的递推公式

最后一步：要么从5往上走2级，要么从6往上走1级；故f(7) = f(5)+f(6)
到达1，向上爬一级；f(1)=1
到达2，从1向上爬一级；直接向上爬两级；f(2)=2

递归方程（递推公式）为：

斐波那契数列：

递归算法

由上列公式自然而然地想到用递归算法，其代码实现一行就足够
public int climbStairs(int n) {
return n==1||n==2?n:climbStairs(n-1)+cimbStairs(n-2)
}

代码递归过程如递归树所示：
这种解法栈的深度太大，leetcode无法通过，超过时间限制。

时间复杂度的推导：

备忘录法

从函数的递归树可以看出有许多项是被重复计算的

针对这种情况，可以用数组保存每一项的值，当递归调用时先判断是否为0，如果是则直接返回，不用再递归重新计算一遍。每项只计算了一遍

示例代码(AC)：
时间复杂度O(n)

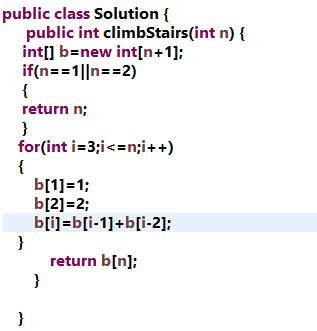
动态规划法

参考：五大常用算法之二：动态规划算法 ]
一、基本概念

动态规划过程是：每次决策依赖于当前状态，又随即引起状态的转移。一个决策序列就是在变化的状态中产生出来的，所以，这种多阶段最优化决策解决问题的过程就称为动态规划。

---

二、基本思想与策略

基本思想与分治法类似，也是将待求解的问题分解为若干个子问题（阶段），按顺序求解子阶段，前一子问题的解，为后一子问题的求解提供了有用的信息。在求解任一子问题时，列出各种可能的局部解，通过决策保留那些有可能达到最优的局部解，丢弃其他局部解。依次解决各子问题，最后一个子问题就是初始问题的解。

由于动态规划解决的问题多数有重叠子问题这个特点，为减少重复计算，对每一个子问题只解一次，将其不同阶段的不同状态保存在一个二维数组中。

与分治法最大的差别是：适合于用动态规划法求解的问题，经分解后得到的子问题往往不是互相独立的（即下一个子阶段的求解是建立在上一个子阶段的解的基础上，进行进一步的求解）。

AC代码：

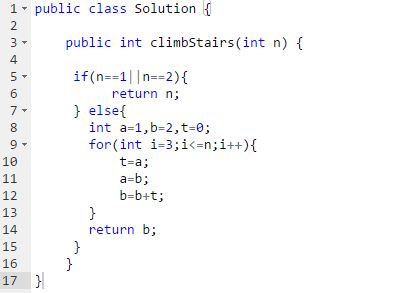
状态压缩法

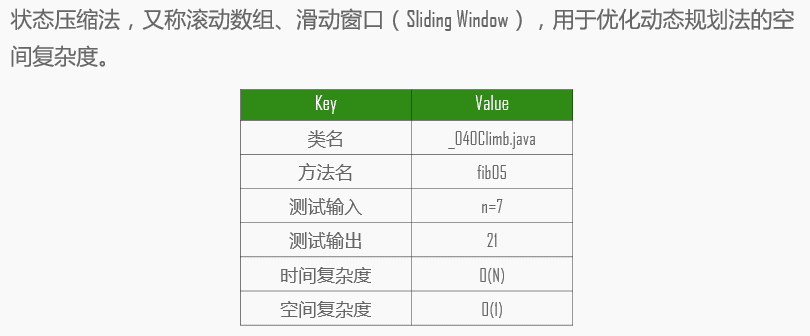
动态规划的解法中数组完全可以用几个变量表示，大大节省了内存空间。

AC代码：
时间O（n），空间O（1）

斐波那契数列的通项公式

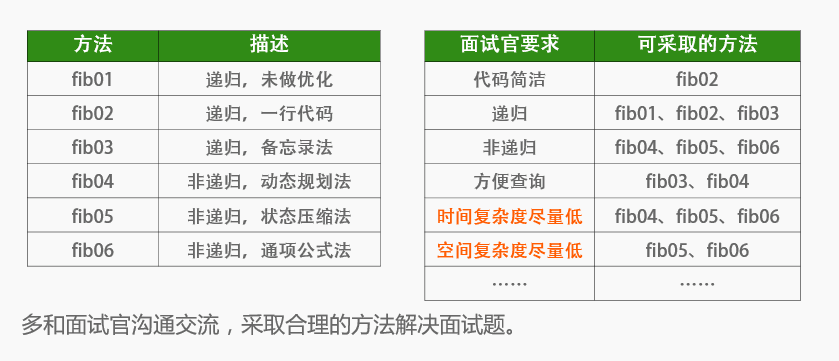
五、简单递归总结

不同要求及相应解法汇总：

代码汇总：

/**
*爬楼梯问题
*/
public class _040Climb {
public int count=0;
/**
*递归算法
*/
public int fib01(int n){
count++;
if(n==1||n==2){
//System.out.println(n);
return n;
}else{
int k=fib01(n-1)+fib01(n-2);
//System.out.println(n);
return k;
}
}
/**
* 递归算法 一行
*/
public int fib02(int n){
return n==1||n==2?n:fib02(n-1)+fib02(n-2);
}
public int dfs(int n,int[] array){
if(array[n]!=0){
return array[n];
}else{
array[n]=dfs(n-1, array)+dfs(n-2, array);
return array[n];
}
}
/**
* 备忘录法
*/
public int fib03(int n){
if(n==1||n==2){
return n;
}else{
int[] array=new int[n+1];
array[1]=1;
array[2]=2;
return dfs(n, array);
}
}
/**
* 动态规划法
*/
public int fib04(int n){
if(n==1||n==2){
return n;
}else{
int[] array=new int[n+1];
array[1]=1;
array[2]=2;
for(int i=3;i<=n;i++){
array[i]=array[i-1]+array[i-2];
}
return array[n];
}
}
/**
* 滚动数组
*/
public int fib05(int n){
if(n==1||n==2){
return n;
}else{
int a=1;
int b=2;
int t;
for(int i=3;i<=n;i++){
t=a+b;
a=b;
b=t;
}
return b;
}
}
/**
* 通项公式法
*/
public int fib06(int n){
if(n==1||n==2){
return n;
}else{
double sqrtFive=Math.sqrt(5);
n++;
double a=Math.pow((1+sqrtFive)/2, n);
double b=Math.pow((1-sqrtFive)/2, n);
double result=1/sqrtFive*(a-b);
return (int) Math.floor(result);
}
}