2019牛客暑期多校训练营(第七场)A、B、C、D、E
A - String(暴力)
题意:
链接:https://ac.nowcoder.com/acm/contest/887/A
给你一个01串,让你分成尽可能少的段的个数并且保证每个段字典序最小(这里的字典序最小是经过循环后最小,比如 0110 就不满足最小,因为可以经过循环变成 0011 )
解题思路:
按 01 组合分块,比如: 11001101100100 首先分成: 11 0011 011 001 00 这种形式,然后开始从头枚举,如果后一个字典序比当前最前面的小就可以放在后面,放完后再从后往前暴力验证一遍,就是把尾部的块放到最前面看看字典序是否会变小,变小就不可以。总体来说这样会优化点,也可以直接暴力,先全放一起,然后再暴力往前删除,然后剩下的再暴力....
AC代码:
#include
#define up(i, x, y) for(int i = x; i <= y; i++)
#define down(i, x, y) for(int i = x; i >= y; i--)
#define bug printf("*********\n")
#define debug(x) cout<<#x"=["<> str;
str_len = str.length();
string tmp = "";
for(int i = 0; i < str_len; i++)
{
tmp += str[i];
if(i == str_len - 1 ||
i < str_len - 1 && str[i] == '1' && str[i + 1] == '0')
{
ans[++len] = tmp;
tmp = "";
}
}
for(int i = 1; i <= len; i++)
{
int s = i;
string t = ans[i];
string res = "";
int p = 0; int f = 0;
while(i <= len && t <= ans[i])
{
if(ans[i] > t) f = 1;
res += ans[i];
++i;
}
--i;
int ll = res.length();
int pos = i;
int x = 0;
string pp = "";
while( pos >= s )
{
string tp = pp;
pp = ans[pos];
pp += tp;
string tmp_pp = pp + res.substr(0, res.length() - pp.length() );
// cout << "\n ******* \n" < B - Irreducible Polynomial(数学小知识)
题意:
链接:https://ac.nowcoder.com/acm/contest/887/B
判别多项式是否可约
解题思路:
AC代码:
#include
#define up(i, x, y) for(int i = x; i <= y; i++)
#define down(i, x, y) for(int i = x; i >= y; i--)
#define bug printf("*********\n")
#define debug(x) cout<<#x"=["<= 0) puts("No");
else puts("Yes");
}
}
} C - Governing sand(思维题)
题意:
链接:https://ac.nowcoder.com/acm/contest/887/C
给你n种树木,并且告诉你每一种树的 : 高度(可以有多棵数目相同的树)、移除这棵树的花费、树木的数目。现在让你移除一些数目来使得移除后最高数目占所有数目比例的一半以上(严格的一半以上,不包括一半),问你最少花费。
解题思路:
首先看到这个问题需要思考一个问题,剩下的最高的树的数目占比大于1/2。那么就是说最后答案肯定是有某一个高度的树作为最高的那一棵,假设当剩下的那个最高的树的高度为 H ,这时的花费最少。那么你需要移除比他高的所有的树,如果移除比他高的所有的树木之后,他的比例还未达到 1/2,这时候需要移除比他矮的树,不可以移除自己,这样会使答案变差,因为分子分母同时减一会使其变小。这样的话怎么找那个高度为 H 的呢? 二分?你会发现高度对于答案不满足单调性,不可以二分。由于 n 是 10^5 所以暴力枚举每一种高度的树,然后假设这种高度为最后剩下的最高的高度的树木,然后把比他高的移除如果还不满足占比 1/ 2 再移除一部分比他低的树木。 那么怎么保证时间呢? 首先你先把树的高度从高到底结构体排下序。 从最高的树木开始枚举,你会发现算出移除比他高的树木的总个数和总价值 ,只需要 O(1) 因为直接遍历的时候就可以保存下来,以备后事之需。那么如果移除比他高的树之后,占比还不够1/2以上怎么办?这时候就需要移除比他矮的树木,你会发现移除比他矮的树木时候只需要关注花费。又因为花费是 1 - 200 。所以可以设一个数组 cost [ i ] = j 。 意思是花费为 i 的有 j 棵树木。这样就可以做到 O(200) 的复杂度来计算移除比他矮的树木需要的花费(这时可以按照比例计算出还需要移除几颗比他矮的树),然后直接遍历cost数组就可以。需要注意的是需要一直维护cost,就是比当前高的还有当前的都要从cost中减去。具可以参照AC代码。
如果花费取值比较大,就不可以暴力了,可以用线段树来维护。
AC代码:
#include
#define up(i, x, y) for(ll i = x; i <= y; i++)
#define down(i, x, y) for(ll i = x; i >= y; i--)
#define bug prllf("*********\n")
#define debug(x) cout<<#x"=["< b.h; // 高度从大到小排序
}
ll tot;
int main()
{
while(~scanf("%lld", &n))
{
memset(cost, 0, sizeof(cost));
tot = 0;
ll ans = 1e18;
for(ll i = 1; i <= n; i++)
{
scanf("%lld %lld %lld", &a[i].h, &a[i].c, &a[i].p);
tot += a[i].p; //总树木个数
cost[a[i].c] += a[i].p; //计算 cost 数组
}
sort(a + 1, a + 1 + n, cmp);
pre_cost = 0; // 移除比当前树高的那些树的花费和数目
pre_num = 0;
cur_cost = 0; // 因为有高度相同的树木,高度相同的要看成同一组,都要最为最后的保留的树
cur_num = 0;
for(ll i = 1; i <= n; i++)
{
cur_cost = 0;
cur_num = 0;
while(i < n && a[i].h == a[i + 1].h) // 找高度相同的树木
{
cost[a[i].c] -= a[i].p; // 维护cost,cost只保留比当前树的高度小的那些树的花费和对应的个数,因为这个数组是为了计算移除比当前的树矮的那些树的花费
cur_cost += a[i].c * a[i].p;
cur_num += a[i].p;
i++;
}
// debug(cur_cost);
cost[a[i].c] -= a[i].p; // 找高度相同的树木
cur_cost += a[i].c * a[i].p;
cur_num += a[i].p;
// debug(cur_cost);
// debug(cur_num);
ll k = tot - pre_num;
ll del = k - 2 * cur_num + 1; // 计算还需要删除的树木的个数
del = max(0LL, del);
ll res = pre_cost;
// debug(pre_cost);
for(ll i = 1; i <= 200; i++) // 暴力移除
{
if(!cost[i]) continue;
ll p = min(del, cost[i]);
del -= p;
res += i * p;
if(!del) break;
// cout << res << '\n';
}
ans = min(ans, res);
pre_cost += cur_cost;
pre_num += cur_num;
}
printf("%lld\n", ans);
}
} D - Number(思维水题)
题意:
链接:https://ac.nowcoder.com/acm/contest/887/D
给你 n 和 p 让你输出一个数,它满足是p的倍数,并且有 n 位数字构成,如果不存在输出 'T_T'
解题思路:
构造答案,构造方式: 一个数字P然后后面都跟 0 就可以,比如 n = 5 , p = 7 . 70000 就满足条件如果p的位数比n大则不可能,输出 'T_T'
AC代码:
#include
#define up(i, x, y) for(int i = x; i <= y; i++)
#define down(i, x, y) for(int i = x; i >= y; i--)
#define bug printf("*********\n")
#define debug(x) cout<<#x"=["<> n >> p;
int len_p = log10(p) + 1;
if(n < len_p) puts("T_T");
else
{
cout << p ;
int time = n - len_p;
while(time--) cout << "0" ;
puts("");
}
} E - Find the median(权值线段树+离散化)
题意+解题思路:
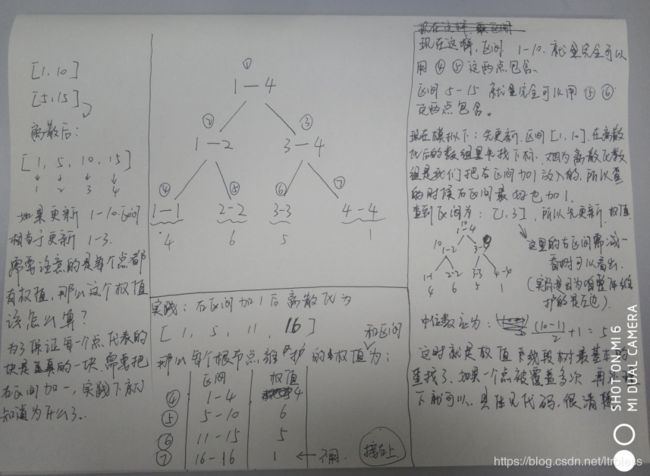
给你一种计算规则,让你计算出 L [ i ] , R [ i ] ,( i 取值是 1 - n )。然后每次增加 L[ i ] - R[ i ] 这些数,然后让你求当前的中位数,如果是偶数个(如 6 个 取第3个)。比如 L[ 1 ] = 5 , R [ 1 ] = 15 . 就会增加 5、6、7 ... ... 13、14、15 这些数。又因为区间大小为 1 - 10^9 比较大,但是 n 是4*10^5。所以可以开一个权值线段树来维护,不过需要对区间离散化来维护。有几个点说一下
举个例子: 有两个区间 [ 1, 10 ] 、[ 5,15 ] ,这时候维护的根节点的值应该什么呢?
AC代码:
#include
#define up(i, x, y) for(ll i = x; i <= y; i++)
#define down(i, x, y) for(ll i = x; i >= y; i--)
#define bug prllf("*********\n")
#define debug(x) cout<<#x"=["<> 1;
build(k << 1, l, mid);
build(k << 1 | 1, mid + 1, r);
push_up(k);
}
void update(ll k, ll l, ll r)
{
if(l <= t[k].l && t[k].r <= r)
{
t[k].sum += t[k].v; // 更新真实权值
t[k].f++;
return ;
}
if(t[k].f) push_down(k);
ll mid = (t[k].l + t[k].r) >> 1;
if(l <= mid) update(k << 1, l ,r);
if(mid + 1 <= r) update(k << 1 | 1, l ,r);
push_up(k);
}
void query(ll k, ll x, ll &ans)
{
if(t[k].l == t[k].r)
{
ll time = t[k].sum / t[k].v; // 被覆盖过 time 次
ll lll = a[ t[k].l ];
ll pos = (x - 1) / time + 1; // 寻找中位数
ans = lll + pos - 1; // 真实中位数大小
return ;
}
if(t[k].f) push_down(k);
if( t[k << 1].sum >= x ) query(k << 1, x, ans);
else
{
query(k << 1 | 1, x - t[k << 1].sum, ans);
}
push_up(k);
}
ll getid(ll x)
{
return lower_bound(a + 1, a + 1 + cnt, x) - a;
}
int main()
{
cnt = 0;
scanf("%lld", &n);
scanf("%lld %lld %lld %lld %lld %lld", &x[1], &x[2], &a1, &b1, &c1, &m1);
scanf("%lld %lld %lld %lld %lld %lld", &y[1], &y[2], &a2, &b2, &c2, &m2);
for(ll i = 3; i <= n; i++)
{
x[i] = (a1 * x[i - 1] + b1 * x[i - 2] + c1) % m1;
y[i] = (a2 * y[i - 1] + b2 * y[i - 2] + c2) % m2;
}
for(ll i = 1; i <= n; i++)
{
l[i] = min(x[i], y[i]) + 1;
r[i] = max(x[i], y[i]) + 1;
a[++cnt] = l[i];
a[++cnt] = r[i] + 1; // 右区间加一
// cout << l[i] << ' ' << r[i] << '\n';
}
// l[1] = 1; l[2] = 5;
// r[1] = 10; r[2] = 15;
// a[1] = l[1]; a[2] = l[2]; a[3] = r[1] + 1; a[4] = r[2] +1;
// cnt = 4;
// n = 2;
sort(a + 1, a + 1 + cnt);
cnt = unique(a + 1, a + 1 + cnt) - a - 1;
// debug(cnt);
a[cnt + 1] = a[cnt] + 1; // 避免最右边根节点建树的时候数组越界
build(1, 1 ,cnt);
ll sum = 0;
for(ll i = 1; i <= n; i++)
{
update(1, getid(l[i]), getid(r[i] + 1) - 1); // 更新区间
ll ans = 0;
sum += r[i] - l[i] + 1; // 累计,计算需要查询第几个数
query(1, (sum - 1) / 2 + 1, ans); // 查询并用ans,保留答案 ((sum - 1) / 2 + 1 --> 代表除2向上取整)
printf("%lld\n", ans);
}
}