算法小题:最大子矩阵问题
目录
- 前言
- 问题描述
- 解法一
- 解法二
- 总结
前言
这次想要总结的求数组(或者二维数组)之间的最优值还有最后一篇最大子矩阵问题。今天把它搞定。
问题描述
解法一
按照正常人的思维水平,如果不是以前对相关知识有了解,首先冲向脑子的解法应该就是暴力遍历了。 你别说,这题暴力解法还真能A出来。不过要做一点小小的优化。 不多说,上代码。
//暴力求解的主要代码
for(i_min = 1;i_min<=n;++i_min)
{
for(int i_max = i_min;i_max<=n;++i_max)
{
for(j_min = 1;j_min<=n;++j_min)
{
for(j_max=j_min;j_max<=n;++j_max)
{
int tmpSum = Sum(i_min,i_max,j_min,j_max); //求(i_min,j_min)-(i_max,j_max)矩形的和
if(maxArea < tmpSum)
{
maxArea = tmpSum;
}
}
}
}
}
分析:简单说一下,就是遍历所有的矩阵的可能,行从i_min到i_max,列从j_min到j_max. 当然把这四个维度的选择遍历出来已经是O(N4)的复杂度了,如果求解矩阵之和也继续暴力的话,那估计肯定是通不过了。
通过简单的分析,我们可以知道,在求解矩阵(假设左上角为(i_min,j_min),右下角为(i_max,j_max))之和的时候,我们可以提前算出来(类似于利用动态规划提前打表了)。
//打表:PS[i][j]:为(1,1),(i,1),(1,j),(i,j)的矩阵之和
void InitPS(int n)
{
//初始化边界值
for(int i = 0;i<=n;++i)
{
PS[i][0] = 0;
PS[0][i] = 0;
}
//计算各个矩阵之和
for(int i = 1;i<=n;++i)
{
for(int j = 1;j<=n;++j)
{
PS[i][j] = PS[i-1][j]+PS[i][j-1]-PS[i-1][j-1]+data[i][j];
}
}
}
//求(i_min,j_min)-(i_max,j_max)矩形的和
int Sum(int i_min,int i_max,int j_min,int j_max)
{
return PS[i_max][j_max] - PS[i_min-1][j_max]-PS[i_max][j_min-1]+PS[i_min-1][j_min-1];
}
解法二
高级一点的算法,那就是要开动我们的小脑袋,发掘一些有用信息了。
由上篇求数组连续的子序列和,可以联想到如果把二维转化为一维,那么就可以利用上篇的算法在O(N)的时间内解决问题了。
so,同样的,外部遍历,我们可以只遍历所有可能的行情况
1-1,1-2,1-3,1-4…
2-2,2-3,2-4,…
3-3,3-4,…
4-4
…
然后对于每一种情况,把所有的行加起来,那不就是一维数组了吗? 然后就可以利用上节中算法在确定两个列界限,最终就可以比较出所有可能的情况了。
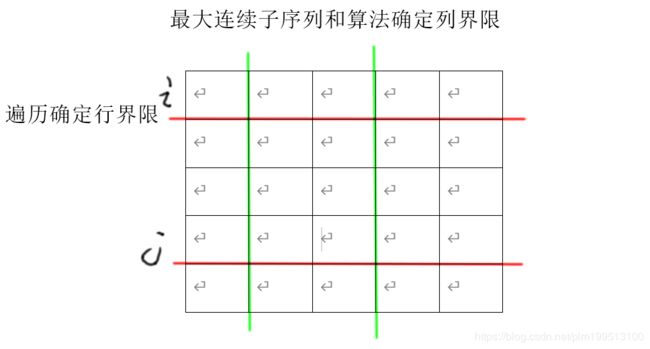
代码如下:
//求解最大子矩阵和
int MatrixMaxSum(int n)
{
int tmpArr[n+1];
int max = INF; //初始化定为最小值
for(int i = 1;i<=n;++i) //遍历所有的行可能
{
for(int j = i;j<=n;++j)
{
for(int k = 1;k<=n;++k)
tmpArr[k] = Sum(i,j,k,k); //第i行到第j行之间,第k列的矩阵和
int retSum = MaxSum(tmpArr,n); //转化为一维数组问题,利用一维数组求解连续子序列和
if(max<retSum)
max = retSum;
}
}
return max;
}
分析:经过上面的改进,算法的复杂度就变成了O(N3)了。注意,上面的代码中Sum函数和解法一是一样的。
总结
好了,又到了激动人心的总结阶段了。今天的总结是,
一般来说,拿到一个问题,我们最先想到的应该是一种比较直接的思路(特殊天才除外)因为这符合我们大脑的学习逻辑,我们要做的就是在规定的时间内,发掘出题目中的信息,进行优化改进。当然,小的改进较为简单,大的改进可能就涉及到思考角度的变化了,也就是那些牛逼的人经常说的:“换个角度思考问题”。

