单源最短路径问题Dijkstra算法的c语言实现
求单源最短路径是图论中比较基本的问题,通常的Dijkstra算法是按阶段进行的,每个节点标有处理和未处理状态的标记,设立一个数组,每个数组中第i个元素为源节点到第i个节点的最短路径(当然,该数组的初值是依照图赋的,邻接节点赋对应边的权值,其他节点赋无穷大)。在Dijkstra算法的每一个阶段,将未处理的节点放入一个集合S,扫描S中距离最小的一个节点v,将v置为处理状态。然后在剩下的所有未处理节点中,对于每个节点w,如果w对应的距离小于v对应的距离加上v到w的距离,则将w对应的距离更新为v对应的距离加上v到w的距离。直到S为空,算法结束。
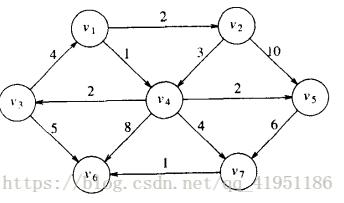
本文换了一种思路,考虑按照层序来遍历节点。我们先来看一下什么是层序。如下图所示(《数据结构与算法分析——c语言描述》fig9.20),令源节点为v1(第一层),因为v2和v4与v1邻接,则可以称v2和v4层序相同,即位于第二层,考虑v2,v4与v5与之邻接,位于第三层序。值的注意的是,v4的层序发生了变化,但这并不影响结果。因为按层序遍历节点只是一种搜索的方式v4在第一层序中已经计算过,但路径不同(第一次是v1->v4,第二次是v1->v2->v4)。显然,v4处的距离值取小的那一个。计算完相同层序的节点后,程序继续计算下一层序的节点,从源节点出发,逐层往外推进。
#include
#include
typedef int Vertex;//图节点编号
#define x 10000 //表示无穷大
#define size 7//节点数目
int Graph[size][size] =
// 1 2 3 4 5 6 7
{
x, 2, x, 1, x, x, x,//1
x, x, x, 3, 10, x, x,//2
4, x, x, x, x, 5, x,//3
x, x, 2, x, 2, 8, 4,//4
x, x, x, x, x, x, 6,//5
x, x, x, x, x, x, x,//6
x, x, x, x, x, 1, x //7
};//图的邻接矩阵表示;
int Graph_Dist[size] = { x,x,x,x,x,x,x };//数组的第i个元素表示从源节点到节点i的最短距离,初始化为无穷大
int Graph_Path[size] = { -1,-1,-1,-1,-1,-1,-1 };//数组的第i个元素表示第i个节点的路径状态,初始化为-1
int Graph_Order[size] = { 0 };//数组的第i个元素代表第i个节点处于的层数
void
Dijkstra(Vertex V0)
{
Vertex V, W;
int Order;
Graph_Path[V0 - 1] = 0;
Graph_Dist[V0 - 1] = 0;
Graph_Order[V0 - 1] = 1;//源点的初始化,层序为1
for (Order = 1; Order <= size; Order++)
{
for (V = 0; V < size; V++)
{
if (Graph_Order[V] == Order)//搜索同一层上的节点
{
for (W = 0; W Graph_Dist[V] + Graph[V][W])
//W与V邻接&&W到源点的距离大于V到源点的距离加上V到W的距离
{
Graph_Dist[W] = Graph_Dist[V] + Graph[V][W];
Graph_Path[W] = V+1;
Graph_Order[W] = Order + 1;
}
}
}
}
}
}
void printarray(int a[]){
for (int i = 0; i < size; i++)
printf("%d ", a[i]);
}
void main()
{
Dijkstra(1);
printarray(Graph_Dist);
}