# cs231n （三）优化问题及方法

cs231n （三）优化问题及方法

标签（空格分隔）： 神经网络

---

0.回顾

cs231n （一）图像分类识别讲了KNN
cs231n （二）讲了线性分类器：SVM和SoftMax

回顾上次的内容，其实就会发现，虽然我们构造好了损失函数，可以简单使用导数的定义解决损失函数优化问题，但是并不高效啊，现在探索一下呗。

1.引言

之前（二部分），我们介绍了图像分类任务中的两个关键部分

1. 评分函数----> 原始图像像素直接映射为评分值：线性函数
2. 损失函数----> 根据分类评分和实际视觉分类差别衡量那个权重矩阵的好坏：SoftMax,SVM.

线性函数的形式是$$f(x_i,W)=W{x}_i$$
SVM实现的公式是：
$$L=\frac{1}{N}\sum _i\sum _{j̸=y_i}[max(0,f(x_i;W{)}_j-f(x_i;W{)}_{y_i}+1)]+\lambda R(W)$$

L 越小，说明这个权重矩阵W越好呗，那么什么时候最小？
很聪明嘛！我们这次讲的就是最优化问题， 这里可真是大(shu)学问。

2. 损失函数是什么东东？

这里讨论的是高维空间重中的：

大声告诉我：CIFAR-10的线性分类权重矩阵大小是多啊？
10x3073呗 （Class X Dimension）另加了一个1.

我能不能看到啊？
比较困难，但我们可以：在1个维度或者2个维度的方向上对高维空间进行分割

• 例如，随机生成一个权重矩阵W，该矩阵就与高维空间中的一个点对应
  然后沿着某个维度方向前进----> 同时记录损失函数值的变化。

• 生成一个随机的方向 $W_1$ 并且沿着此方向计算损失值，计算方法是根据不同的a 值来计算$L(W+a{W}_1)$。

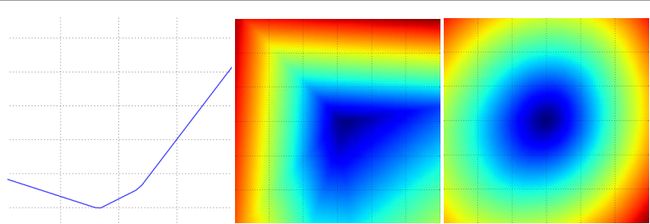
这个过程将生成一个图表，其x轴是a值，y轴是损失函数值。同样的方法还可以用在两个维度上，通过改变a,b来计算损失值 $L(W+a{W}_1+b{W}_2)$，从而给出二维的图像。在图像中，a,b可以分别用x和y轴表示，而损失函数的值可以用颜色变化表示：

一个无正则化的SVM的损失函数就是看上面，左中分别有一个数据，右是10个

左：a值渐变时，及某个维度方向上对应的的损失值变化
中右：蓝色部分是低损失值区域，红色部分是高损失值区域

---

对于一个图像数据，损失函数的计算公式如下：

$$Li=\sum _{j̸=y_i}[max(0,w_j^T{x}_i-w_{y_i}^T{x}_i+1)]$$

假设有一个简单的数据集，其中包含有3个只有1个维度的点，数据集数据点有3个类别。那么完整的无正则化SVM的损失值计算如下：

$$L_0=max(0,w_1^T{x}_0-w_0^T{x}_0+1)+max(0,w_2^T{x}_0-w_0^T{x}_0+1)$$
$$L_1=max(0,w_0^T{x}_1-w_1^T{x}_1+1)+max(0,w_2^T{x}_1-w_1^T{x}_1+1)$$
$$L_2=max(0,w_0^T{x}_2-w_2^T{x}_2+1)+max(0,w_1^T{x}_2-w_2^T{x}_2+1)$$
$$L=(L_0+L_1+L_2)/3$$

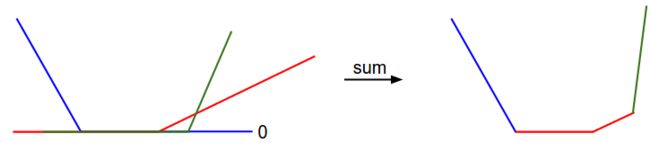
对于一维数据，$x_i$和权重$w_j$都是数字,从$w_0$，可以看到上面的式子中一些项是$w_0$的线性函数，且每一项都会与0比较，取两者的最大值。

那么：x轴方向就是一个权重，y轴就是损失值

每个部分 1.是某个权重的独立部分，2.是该权重的线性函数与0阈值的比较。完整的SVM数据损失就是这个形状的30730维版本(3073*10).

对：就是凸函数 ，人家还出了课程:最优化凸函数
由于max，则SVM函数产生不可导的点，那么这个损失函数不可微，所以梯度没有意义，这里用到了次梯度。

3. 最优化

失函数可以量化某个具体权重集W的质量，最优化的目标：到能够最小化损失函数值的W

办法1：随机搜索（不好）

随机尝试很多不同的权重，然后看其中哪个最好，就是瞎蒙呗，你想想能好么？

# X_train的每一列都是一个数据样本（3073 x 50000的数组）
# Y_train是数据样本的类别标签（1x50000的数组）
# 函数L即损失函数

bestloss = float("inf") # Python assigns the highest possible float value
for num in xrange(1000):
  W = np.random.randn(10, 3073) * 0.0001 # generate random parameters
  loss = L(X_train, Y_train, W) # get the loss over the entire training set
  if loss < bestloss: # keep track of the best solution
    bestloss = loss
    bestW = W
  print 'in attempt %d the loss was %f, best %f' % (num, loss, bestloss)

# in attempt 0 the loss was 9.401632, best 9.401632
# in attempt 1 the loss was 8.959668, best 8.959668
# in attempt 2 the loss was 9.044034, best 8.959668
# in attempt 3 the loss was 9.278948, best 8.959668
# in attempt 4 the loss was 8.857370, best 8.857370
# in attempt 5 the loss was 8.943151, best 8.857370
# in attempt 6 the loss was 8.605604, best 8.605604
# ... (trunctated: continues for 1000 lines)

结果可想而知，L是有大有小，不管怎么样，先用测试集试试

# Assume X_test is [3073 x 10000], Y_test [10000 x 1]
scores = Wbest.dot(Xte_cols) # 10 x 10000, the class scores for all test examples
# find the index with max score in each column (the predicted class)
Yte_predict = np.argmax(scores, axis = 0)
# and calculate accuracy (fraction of predictions that are correct)
np.mean(Yte_predict == Yte)
# returns 0.1555

表现最好的权重W跑测试集的准确率是15.5%，瞎蒙就是10%，好学生!

关键思路：迭代优化： 从一个随机的W开始，然后迭代，每次都让它的损失值变得更小一点, 还是在尝试。

蒙眼山林猎人：蒙着眼睛回家（山底）， 那就滚呗，哈哈。

办法2：随机本地试探

还是蒙着眼睛，超每个方向都试一下，如果感觉自己下降了，那就走那个方向啦。
看专家怎么说的：随机的扰动$\delta W $，只有当$W+\delta$ W的损失值变低，我们才会更新损失。

嗯，大家都是凡人。

W = np.random.randn(10, 3073) * 0.001 # 随机 初始值：W 
bestloss = float("inf")
for i in xrange(1000):
  step_size = 0.0001
  Wtry = W + np.random.randn(10, 3073) * step_size
  loss = L(Xtr_cols, Ytr, Wtry)
  if loss < bestloss:
    W = Wtry
    bestloss = loss
  print 'iter %d loss is %f' % (i, bestloss)

这个方法得到21.4%的分类准确率。这个比策略一好，但是依然过于浪费计算资源，但是累还耗时。

方法3：跟随梯度—>望眼欲穿法

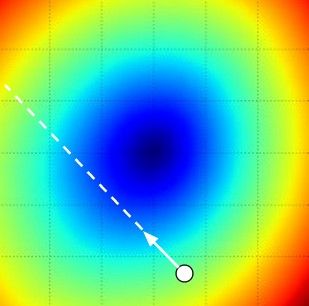
这次是睁开眼睛，你就往下看啊，越陡你下山越快，回家越快啊，小心别掉坑里啊。

数学专家：从数学上计算出最陡峭的方向。这个方向就是损失函数的梯度（gradient），这个方法就好比是感受我们脚下山体的倾斜程度，然后向着最陡峭的下降方向下山。

在一维函数中，斜率是函数在某一点的瞬时变化率. 梯度是函数的斜率的一般化表达，它不是一个值，而是一个向量。在输入空间中，梯度是各个维度的斜率组成的向量（或者称为导数derivatives）。对一维函数的求导公式如下：

$$\frac{df(x)}{dx}=\underset{h\to 0}{\lim }\frac{f(x+h)-f(x)}{h}$$
当函数有多个参数的时候，我们称导数为偏导数。而梯度就是在每个维度上偏导数所形成的向量,多个参数的时候，我们称导数为偏导数.(我就叫它偏头痛)。哼~~~

4. 梯度计算

算梯度有两种方法：一个是缓慢的近似方法（数值梯度法），但实现相对简单。另一个方法（分析梯度法）计算迅速且精确，但是确实容易出错，且需要使用微分。

大白话就是: 一个是慢一点像老头一样一点一点的挪，一个是很快啊纵深一跃，容易骨折我真的没写错字，。

• 利用有限差值计算
  下面代码输入函数f和向量x，计算f的梯度的通用函数，返回函数f在点x处的梯度。

def eval_numerical_gradient(f, x):
  """ 
  a naive implementation of numerical gradient of f at x 
  简单的实现梯度
  - f should be a function that takes a single argument
  只有一个参数
  - x is the point (numpy array) to evaluate the gradient at
  计算梯度的位置
  """ 
  
  # 原点计算函数值
  fx = f(x) # evaluate function value at original point
  grad = np.zeros(x.shape)
  h = 0.00001

  # iterate over all indexes in x
  # 来啊， 挪啊（迭代啦~~）
  it = np.nditer(x, flags=['multi_index'], op_flags=['readwrite'])
  while not it.finished:

    # evaluate function at x+h
    # 挪了一步之后的海拔（x+h处的值）
    ix = it.multi_index
    old_value = x[ix]
    x[ix] = old_value + h # increment by h（再挪一步，更新）
    fxh = f(x) # evalute f(x + h)
    
    # 记住你的海拔，太重要了
    x[ix] = old_value # restore to previous value (very important!)
    
    # compute the partial derivative
    # 计算偏导数
    grad[ix] = (fxh - fx) / h # the slope
    it.iternext() # step to next dimension

  return grad

概括一下回家过程：先对所有维度进行迭代，每个维度上会产生一个很小的变化h，通过观察函数值变化，计算函数在该维度上的偏导数，最后把所有的梯度存储在变量grad中。

**实践一下：**我们一般用 1e-5来表示h,反正就是很小啦，其实我们还可以用：$[f(x+h)-f(x-h)]/2h$更好，细节。

计算权重空间中的某些随机点上，CIFAR-10损失函数的梯度：

# 要使用上面的代码我们需要一个只有一个参数的函数(直译)
# 在这里参数就是权重，所以包含X_train和Y_train
def CIFAR10_loss_fun(W):
  return L(X_train, Y_train, W)

W = np.random.rand(10, 3073) * 0.001 # 随机权重向量
df = eval_numerical_gradient(CIFAR10_loss_fun, W) # 得到梯度

梯度就是每个维度的斜率，以此来更新

loss_original = CIFAR10_loss_fun(W) # the original loss
print 'original loss: %f' % (loss_original, )

# lets see the effect of multiple step sizes
for step_size_log in [-10, -9, -8, -7, -6, -5,-4,-3,-2,-1]:
  step_size = 10 ** step_size_log
  W_new = W - step_size * df # new position in the weight space
  loss_new = CIFAR10_loss_fun(W_new)
  print 'for step size %f new loss: %f' % (step_size, loss_new)

# prints:
# original loss: 2.200718
# for step size 1.000000e-10 new loss: 2.200652
# for step size 1.000000e-09 new loss: 2.200057
# for step size 1.000000e-08 new loss: 2.194116
# for step size 1.000000e-07 new loss: 2.135493
# for step size 1.000000e-06 new loss: 1.647802
# for step size 1.000000e-05 new loss: 2.844355
# for step size 1.000000e-04 new loss: 25.558142
# for step size 1.000000e-03 new loss: 254.086573
# for step size 1.000000e-02 new loss: 2539.370888
# for step size 1.000000e-01 new loss: 25392.214036

梯度负方向更新：我们要下坡呢

步长： 这个不好选择啊，步子迈太大，扯淡啊。。。太小？回到家，老婆都和人跑了。

目前为止，时快时慢好像是最好的选择，并且这样效率很低哇。。。

5. 微分分析计算梯度

这里做了一个近似，因为定义来说是，h值越小越好啊，所以我们要时不时的看看自己是不是下降了（梯度检查），我们试试新办法。

用SVM的损失函数在某个数据点上的计算来举例：

$$L_i=\sum _{j̸=y_i}[max(0,w_j^T{x}_i-w_{y_i}^T{x}_i+\Delta )]$$
可以对函数进行微分。比如，对$w_{y_i}$进行微分得到：

$${\nabla }_{w_{y_i}}{L}_i=-(\sum _{j̸=y_i}1(w_j^T{x}_i-w_{y_i}^T{x}_i+\Delta >0))x_i$$

其中1是一个示性函数，如果括号中条件为真，那么函数值为1，反之，则函数值为0. 这个可不是很简单的1喔！！！

公式唬人，代码实现的时候比较简单：只需计算对损失函数产生了贡献分类的数量，然后乘以$x_i$就是梯度了。这个梯度只是对应正确分类的W的行向量的梯度，那些$j̸=y_i$行的梯度是：

$${\nabla }_{w_j}{L}_i=1(w_j^T{x}_i-w_{y_i}^T{x}_i+\Delta >0)x_i$$

6. 梯度下降

计算梯度，然后更新

# 普通梯度下降

while True:
  weights_grad = evaluate_gradient(loss_fun, data, weights)
  weights += - step_size * weights_grad # 梯度更新

梯度下降是对神经网络的损失函数最优化中最常用的方法, 我们一直跟着梯度走，直到结果不再变化.

7. 小批量数据梯度下降（Mini-batch GD）：

批量干活效果好，因为：训练集中的数据都是相关的！

# 普通的小批量数据梯度下降

while True:
  data_batch = sample_training_data(data, 256) # 256个数据
  weights_grad = evaluate_gradient(loss_fun, data_batch, weights)
  weights += - step_size * weights_grad # 参数更新

如果批量是一个呢？
聪明，就是随机梯度下降啦！（SGD）
小批量数据的大小是一个超参数，但是一般并不需要通过交叉验证来调参！开心，有木有！！！

tricks

使用比如32，64，128batch，因为在实际中许多向量化操作实现的时候，输入数据量是2的倍数，那么运算更快。

回到家了，总结时间，老婆让总结一下山林冒险

8. Summary

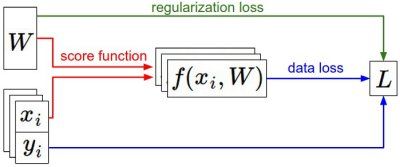
信息流图（路线图），数据集中的(x,y)是确定的，
权重：是随机开始（后期迁移学习就不是啦），
评分：评分函数计算出来存储在f中
损失：数据损失，和正则化损失。

数据损失计算的是：分类评分f和实际标签y之间的差异
正则化损失是：一个关于权重的函数（ 其实一般就只计算这里啦 ）

理解、计算损失函数关于权重的梯度，这个可是设计、训练和理解神经网络的核心能力。

下节课介绍反向传播！

转载和疑问声明

如果你有什么疑问或者想要转载，没有允许是不能转载的哈
赞赏一下能不能转？哈哈，联系我啊，我告诉你呢 ~~
欢迎联系我哈，我会给大家慢慢解答啦~~~怎么联系我？ 笨啊~ ~~ 你留言也行

你关注微信公众号1.机器学习算法工程师：2.或者扫那个二维码，后台发送 “我要找朕”，联系我也行啦！

（爱心.gif） 么么哒 ~么么哒 ~么么哒
码字不易啊啊啊，如果你觉得本文有帮助，三毛也是爱！

我祝各位帅哥，和美女，你们永远十八岁，嗨嘿嘿~~~