可能是关于 kNN 算法最详细的入门总结
【从零开始学机器学习第 10 篇】
摘要:机器学习最简单算法——kNN 算法总结。
对于不少想学机器学习的初学者来说,可能听到「机器学习」四个字就有点发怵,觉得难学门槛高,既要会编程数学还要好,那些科班出身的研究生才干得了。
这话也对也不对,要说它对是因为要学的内容的确不少也不简单,远不像数据分析、爬虫看着好学。其次,学习路径一定程度地被魔化了:很多人说学机器学习要先去啃《西瓜书》、《统计学习方法》这些大篇幅的数学公式算法书,很容易让新手放弃。
要说它不对也有道理。一是可能你并没有真正想去学它,没发现它有用或者至少有趣的地方;二是机器学习真的没有那么难入门,前提是找到合适自己的方法。所以想清楚为什么学和从哪儿开始学很重要。
看了很多教程后,找到了合适自己的机器学习入门方法,也觉得适合很多人,接下来会一点点分享出来。
作为入门的第一课,kNN 算法是最好的选择,因为它是机器学习中最简单的算法,学会它几乎没有难度只需要会两点:高中数学和一点 Python 编程基础(远没有爬虫那么难)。
虽然是最简单的算法,但我们还是花了大量篇幅(9 篇文章)来介绍它,为的是打好基础,今天这一篇做个总结。
kNN 算法(K-Nearest Neighbor),也叫 K 近邻算法,在具体介绍它之前,记住它的两个特点。
它有什么用途?主要有两种。
一是可以解决分类问题,比如预测红酒属于哪一类,花属于哪一种,是良性肿瘤还是恶性肿瘤等。除了二分类,它还可以解决多分类问题。
二是可以解决回归问题,比如预测房价多少、学生成绩多高等。
kNN 算法是少数能同时解决分类和回归问题的算法,很实用。
它的算法思想和实现难么?非常简单。
kNN 算法思想可以用「近朱者赤近墨者黑」形容,谁离待预测值近,待预测值就属于哪一类,就这么简单。判断远近可以用中学学过的欧拉距离公式计算。
知道特点后,我们通过一个酒吧猜酒的例子引入了 kNN算法:桌上倒的红酒属于两类,需要根据它们的颜色深度、酒精浓度值去预测新倒的酒属于哪一类:
【机器学习01】Python 手写机器学习最简单的 kNN 算法(可点击)

具体如何预测呢?很简单,只需要两步:先把场景抽象为数学问题,然后将数学问题写成 Python 代码得到预测结果。
抽象为数学问题就是把酒映射到坐标轴中,接着根据欧拉公式计算待预测酒(黄色点)同每杯样本酒(红绿色点)之间的距离,然后排序并取前 k 杯酒(k 个点),哪一类酒占比多,则新倒的酒就归属哪一类。

理清数学思路后就可以手写代码,手写代码可以加深对算法的理解,同时也能搞懂 Sklearn 调包背后的真正含义。
在这第一篇文章中,我们就手写了 kNN 算法,预测出新倒的酒(黄色点)属于绿色的赤霞珠。
接下来为了作对比,我们又调用了 Sklearn 中的 kNN 算法包,仅 5 行代码就得到了相同的结果。
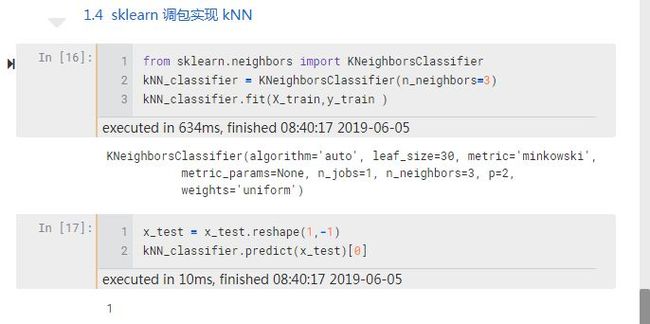
初次接触 sklearn 的话,可能并不清楚代码背后的 fit、predict 做了什么,于是我们仿写了 Sklearn 的 kNN 算法包,加深了对 Sklearn 调包的理解:
【机器学习02】sklearn 中的 kNN 封装算法实现
通过以上两篇我们就初步学会了 kNN 算法。不过在对算法做预测时,使用了全部数据作为训练集,这样一来算法的预测准确率如何并不清楚。
所以我们做了改进,将数据集拆成一大一小两部分,大的作为训练集,小的作为测试集。在训练集上训练好 kNN 模型后,把测试集喂给它得到预测结果,接着和测试集本身的真实标签值作比较,得到了模型的准确率。
这一过程用到了 sklearn 的 train_test_split 方法,最终将一份有 178 个样本的葡萄酒数据集,按照 7:3 的比例随机划分出了 124 个训练样本和 54 个测试样本。
【机器学习03】手写 Sklearn 的 train_test_split 函数
具体如何计算模型的分类准确率呢?我们又用到了 sklearn 的 accuracy_score 方法,在葡萄酒数据集上达到了 76% 的准确率 。(54 个测试样本中,预测对了 41 个)
【机器学习04】Sklearn 的 model.score 和 accuracy_score 函数
为了巩固之前 4 节内容,我们又以两个机器学习中常见的数据集为例:鸢尾花和手写数字识别,初步走了一遍 kNN 分类算法。
【机器学习05】kNN小结:解决鸢尾花和手写数字识别分类

最后,模型在鸢尾花数据集上的准确率达到 97.8%(45 个花样本仅预测错 1 个),在手写数字数据集上的预测准确率达到了 98.7%。这是在使用默认参数而未调参的情况下得到的结果,可见 kNN 算法虽简单但效果很好。
不过,我们又发现存在一个问题:kNN 模型有很多参数(叫超参数),我们使用的都是默认参数,这样建立得到的模型不一定是最好的,而我们期望找到最好的模型。
如何做到呢?这就需要调参,于是我们了解了 kNN 算法几个重要的超参数,手动搭配组合之后找到了更好的模型,分类准确率进一步提升:
【机器学习06】调参——得到更好的 kNN 模型

但手动调整超参数很不方便,为此我们想到了 Sklearn 中专门实现调参功能的网格搜索方法(GridSearchCV),只需要指定超参数范围,它就会运行所有超参数组合建立模型,最后返回其中效果最好的一组,这比我们自己手写的方法方便地多。
【机器学习07】使用网格搜索(GridSearchCV)快速找到 kNN 模型最佳超参数
通过网格搜索我们进一步优化了 kNN 模型,这并没有完,还有很重要的一点工作:对数据做归一化处理。因为 kNN 模型跟样本距离有密切关系,如果特征之间的数量级相差很大的话,在计算距离时就容易产生偏差影响分类效果,所以最好建模前先去除数据量纲。
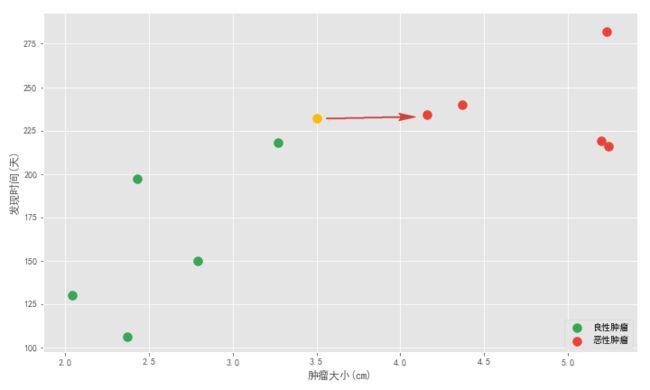 原始特征
原始特征
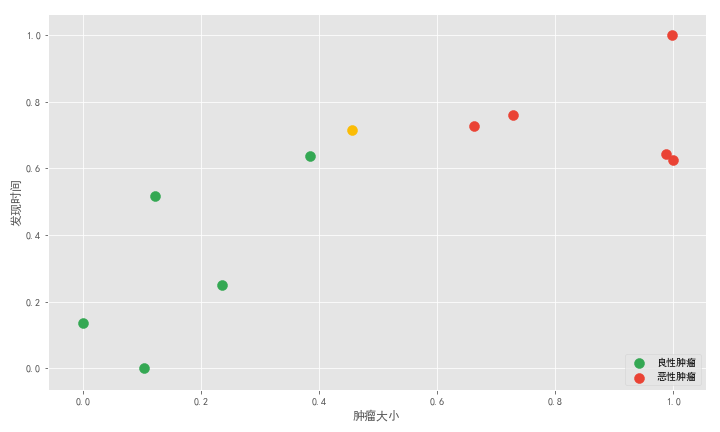 最值归一化后
最值归一化后
 均值方差归一化后
均值方差归一化后
常用的数据归一化方式有最值归一化和均值方差归一化,详细对比了两种方法的特点,最终建议使用均值方差归一化:
【机器学习08】数据归一化 Feature Scaling
归一化处理后,之前葡萄酒模型的分类准确率从最初的 0.76 飙升到了 0.96。(54 个测试样本中,正确分类的样本数从 41 个上升到 52 个),可见数据归一化对 kNN 算法的重要性。
以上我们主要介绍的是 kNN 算法解决分类问题,它还可以解决回归问题,方法大同小异。为了加深理解,我们以常见的回归数据集波士顿房价为例,运用 kNN 回归模型预测了房价,效果不错。
【机器学习09】kNN 解决回归问题:以波士顿房价为例
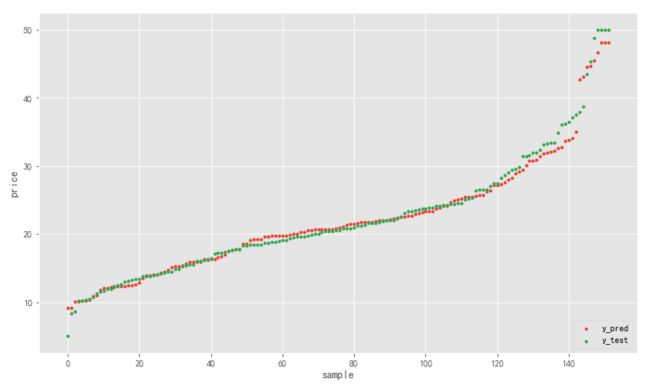
以上就是 kNN 算法的主要内容,最后总结一下 kNN 算法的特点:
优点:
可解决二分类和多分类问题(一些算法只能解决二分类问题)
可解决回归问题(部分算法只能解决分类问题,解决不了回归问题)
算法简单效果好
缺点:
计算耗时
kNN 算法在计算样本距离时,每个样本都要遍历计算一篇全部训练样本,当数据量很大时,会很耗时,虽然可以用 KD 树、球树等改进方法但效率依然不高。
对异常值敏感
kNN 算法预测结果依赖最近的 K 个点,一旦 K 个点之中有异常值,很可能会分类错误。
预测结果不具有可解释性
对于预测的结果,并不能解释预测值为什么属于这个类别。不像线性回归算法具有可解释性。
维数灾难
随着维度的增加,“看似相近”的两个点,它们之间的距离会随着特征维数的增多而越来越大。比如有 2 个特征的数据集,两个点之间的距离是1.4,一旦特征数量增大到 10000 维时,距离就变成了 100。
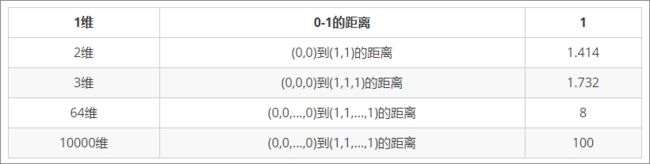
相信看完这十篇文章,应该就可以搞明白 kNN 算法了,也能看得懂李航《统计学习方法》第 3 章的 kNN 算法。
到这儿,你就迈出了机器学习的第一步。接下来一起学习第二个算法吧:线性回归。
最后以上所有文章代码,可以在下方公众号中回复:knn 得到。

