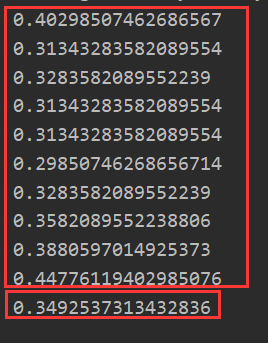
回顾:
梯度下降
梯度下降和梯度上升区别
一:加载数据和实现sigmoid函数(同梯度下降)
import numpy as np def loadDataSet(): data = np.loadtxt("testSet.txt") data_X = data[:,0:2] data_Y = data[:,-1] #注意,后面需要有一个常数项x0,设置为1即可 data_X = np.c_[np.ones(data_X.shape[0]),data_X] return data_X,np.array([data_Y]).T def sigmoid(Z): return 1/(1+np.exp(-Z))
二:实现批量梯度上升(重点)
(一)代码实现
def gradientAsc(data_X,data_Y,iter_Count,alpha): #使用梯度上升,不需要求解代价函数,利用的是概率---我们想求概率最大值 及误差最小 这里就体现了我们之前提及的sigmoid不只是表示0/1,还是一个表示概率的函数 m,n = data_X.shape W = np.ones((n,1)) #初始化权重矩阵 这里直接是n行1列 for i in range(iter_Count): #进行迭代 yPred = sigmoid(data_X@W)#开始计算sigmoid值---即预测值 error = data_Y - yPred #获取实际标签值和预测值的误差 W += alpha*data_X.T@error #其中梯度上升---我们这里的W一直在上升,注意:yPred由于来自sigmoid函数,所以会一直<=1,所以error不会为负值,可能最后拟合出error正好为全0的结果,就是我们要的结果 return W
(二)结果预测
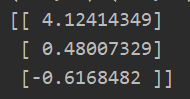
data_X,data_Y = loadDataSet() print(gradientAsc(data_X,data_Y,500,0.001))
三:绘制图像决策边界
#绘图图像,画出决策边界 plt.figure() plt.scatter(data_X[np.where(data_Y==1),1],data_X[np.where(data_Y==1),2],c="red",s=30) plt.scatter(data_X[np.where(data_Y==0),1],data_X[np.where(data_Y==0),2],c="green",s=30) #绘制决策边界直线 x = np.linspace(-3,3,100) y = -(W[0]+W[1]*x)/W[2] plt.plot(x,y) plt.show()
四:随机梯度下降法
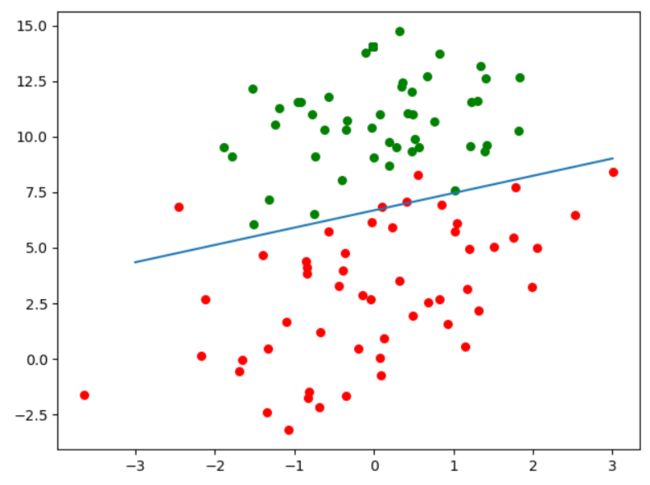
(一)简陋版随机梯度下降法
def stocGradientAsc(data_X,data_Y,alpha): #随机梯度算法(简陋版) m,n = data_X.shape W = np.ones((n,1)) for i in range(m): #循环的次数和批量随机梯度下降不一致 h = sigmoid(data_X[i]@W) #这里选择一个数据,获取预测(没体现随机) error = data_Y[i] - h W += alpha*error*(np.array([data_X[i]]).T) return W data_X,data_Y = loadDataSet() W = stocGradientAsc(data_X,data_Y,150,0.01) #绘图图像,画出决策边界 plt.figure() plt.scatter(data_X[np.where(data_Y==1),1],data_X[np.where(data_Y==1),2],c="red",s=30) plt.scatter(data_X[np.where(data_Y==0),1],data_X[np.where(data_Y==0),2],c="green",s=30) #绘制决策边界直线 x = np.linspace(-3,3,100) y = -(W[0]+W[1]*x)/W[2] plt.plot(x,y) plt.show()
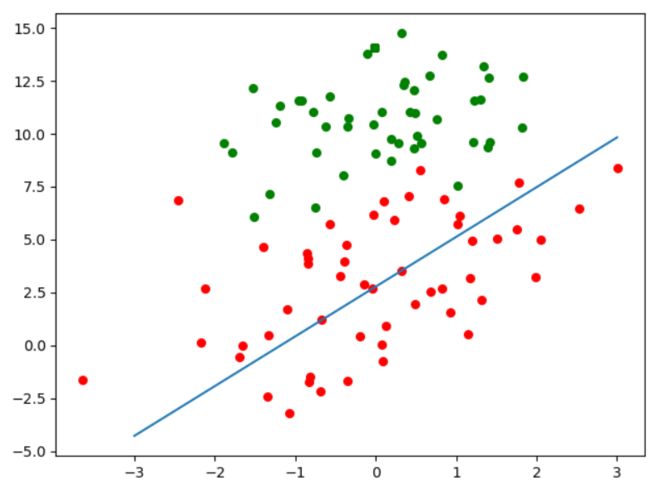
(二)改进版随机梯度下降法
def stocGradientAsc2(data_X,data_Y,iter_Count,alpha): m,n = data_X.shape W = np.ones((n,1)) for j in range(iter_Count): #迭代次数和批量随机梯度保持一致 dataInt = list(range(m)) #获取全部索引0 - m-1 列表 for i in range(m): #迭代数据和批量保持一致 new_alpha = 4/(1+j+i)+alpha #适当调整alpha参数,随着迭代次数上升,适当降低alpha的值。防止后面的波动。并且避免参数严格下降 randIdx = int(random.uniform(0,len(dataInt))) #uniform随机选取范围内的一个实数,所以要int h = sigmoid(data_X[randIdx]@W) error = data_Y[randIdx] - h W += new_alpha*error*np.array([data_X[randIdx]]).T del(dataInt[randIdx]) return W data_X,data_Y = loadDataSet() W = stocGradientAsc2(data_X,data_Y,150,0.01) #绘图图像,画出决策边界 plt.figure() plt.scatter(data_X[np.where(data_Y==1),1],data_X[np.where(data_Y==1),2],c="red",s=30) plt.scatter(data_X[np.where(data_Y==0),1],data_X[np.where(data_Y==0),2],c="green",s=30) #绘制决策边界直线 x = np.linspace(-3,3,100) y = -(W[0]+W[1]*x)/W[2] plt.plot(x,y) plt.show()
五:从疝气病症预测病马的死亡率
(一)数据导入
import random import numpy as np import matplotlib.pyplot as plt def loadDataSet(): #获取训练集 data = np.loadtxt("horseColicTraining.txt") m,n = data.shape trainData_X = data[:,0:n-1] trainData_X = np.c_[np.ones(m),trainData_X] trainData_Y = np.array([data[:,n-1]]).T #注意,后面需要有一个常数项x0,设置为1即可 #获取测试集 data = np.loadtxt("horseColicTest.txt") m, n = data.shape TestData_X = data[:, 0:n-1] TestData_X = np.c_[np.ones(m),TestData_X] TestData_Y = np.array([data[:, n-1]]).T return trainData_X,trainData_Y,TestData_X,TestData_Y
(二)改进sigmoid函数
def sigmoid(Z): if Z >= 0: return 1/(1+np.exp(-Z)) #-Z可能会是极大值,所以导致np.exp(-Z)过大,导致溢出。所以由下面分支处理 else: #若是Z<0,那么会出现结果为0。我们只是将上面的式子展开来了。这样,不会出现np.exp(-Z)过大溢出 return np.exp(Z) / (1+np.exp(Z))
(三)实现预测误差率
def stocGradientAsc2(data_X,data_Y,iter_Count,alpha): m,n = data_X.shape W = np.ones((n,1)) for j in range(iter_Count): #迭代次数和批量随机梯度保持一致 dataInt = list(range(m)) #获取全部索引0 - m-1 列表 for i in range(m): #迭代数据和批量保持一致 new_alpha = 4/(1+j+i)+alpha #适当调整alpha参数,随着迭代次数上升,适当降低alpha的值。防止后面的波动。并且避免参数严格下降 randIdx = int(random.uniform(0,len(dataInt))) #uniform随机选取范围内的一个实数,所以要int h = sigmoid(data_X[randIdx]@W) error = data_Y[randIdx] - h W += new_alpha*error*np.array([data_X[randIdx]]).T del(dataInt[randIdx]) return W def classifyVector(PreDataVec,W): h = sigmoid(PreDataVec@W) if h > 0.5: return 1 else: return 0 def OneTestGetErr(trainData_X,trainData_Y,TestData_X,TestData_Y): W = stocGradientAsc2(trainData_X,trainData_Y,500,0.01) err = 0 for i in range(TestData_X.shape[0]): if classifyVector(TestData_X[i],W) != TestData_Y[i]: err += 1 return err / TestData_X.shape[0] def GetAvgErr(trainData_X,trainData_Y,TestData_X,TestData_Y,TestNums=10): ErrAvg = 0.0 for i in range(TestNums): err = OneTestGetErr(trainData_X,trainData_Y,TestData_X,TestData_Y) print(err) ErrAvg += err return ErrAvg / TestNums trainData_X,trainData_Y,TestData_X,TestData_Y = loadDataSet() print(GetAvgErr(trainData_X,trainData_Y,TestData_X,TestData_Y))