机器学习数据不平衡问题及其解决方法

数据不平衡是机器学习任务中的一个常见问题。真实世界中的分类任务中，各个类别的样本数量往往不是完全平衡的，某一或某些类别的样本数量远少于其他类别的情况经常发生，我们称这些样本数量较少的类别为少数类，与之相对应的数量较多的类别则被称为多数类。在很多存在数据不平衡问题的任务中，我们往往更关注机器学习模型在少数类上的表现，一个典型的例子是制造业等领域的缺陷产品检测任务，在这个任务中，我们希望使用机器学习方法从大量的正常产品中检测出其中少数几个存在缺陷的产品，有缺陷产品在所有产品中的占比可能只有十分之一或者百分之一甚至更低。在这个例子里，我们只关心机器学习模型对少数类（有缺陷产品）的查准率和查全率，并不在意模型在多数类（正常产品）上的表现。

1、为什么需要解决数据不平衡问题

1.1 分类器性能下降

在数据不平衡的情况下，少数类样本的数量远少于多数类样本，会产生更多的稀疏样本（那些样本数很少的子类中的样本）。由于缺乏足够的数据，分类器对稀疏样本的刻画能力不足，难以有效的对这些稀疏样本进行分类。数据不均衡导致的分类器决策边界偏移也会影响到最终的分类效果。这里以SVM为例，少数类和多数类的每个样本对优化目标的贡献都是相同的，但由于多数类样本的样本数量远多于少数类，最终学习到的分类边界往往更倾向于多数类，导致分类边界偏移的问题。下图给出了在一个三分类问题中，不同的数据不平衡程度对应的分类器分类效果示意。从图中可以看出，随着数据不平衡程度的增加，分类器分类边界偏移也逐渐增加，导致最终分类性能下降明显。

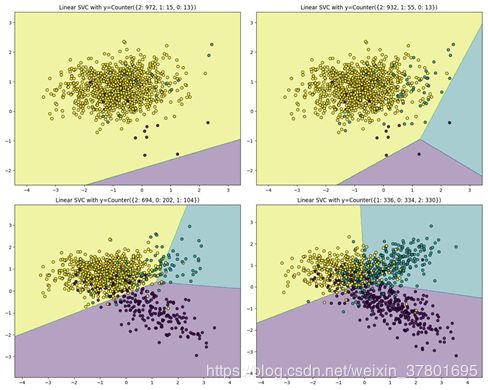
像逻辑回归或随机森林这样开箱即用的分类器，倾向于通过舍去稀有类来泛化模型。

在一个二分类问题中，训练集中class 1的样本数比class 2的样本数是60:1。使用逻辑回归进行分类，最后结果是其忽略了class 2，即其将所有的训练样本都分类为class 1。

在分类任务的数据集中，有三个类别，分别为A，B，C。在训练集中，A类的样本占70%，B类的样本占25%，C类的样本占5%。最后我的分类器对类A的样本过拟合了，而对其它两个类别的样本欠拟合。

1.2 评价指标不适用

当你在对一个类别不均衡的数据集进行分类时得到了90%的准确度（Accuracy）。当你进一步分析发现，数据集的90%的样本是属于同一个类，并且分类器将所有的样本都分类为该类。在这种情况下，显然该分类器是无效的。并且这种无效是由于训练集中类别不均衡而导致的。

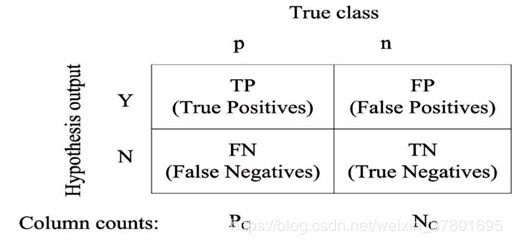
可以看到，在计算accuracy时，TP和TN是完全等价的，即每个类别的样本对accuracy的贡献是相同的，在数据不均衡的情况下，accuracy难以体现模型对少数类的分类效果，不适合直接使用。

相对于accuracy来说，在数据不平衡的情况下，precision, recall、F、 ROC曲线和ROC AUC值不会受到数据分布的影响，可以更有效的反应分类模型在特定类别上，尤其是少数类上的分类性能。

2、 解决数据不平衡问题的方法

2.1 从数据上解决

2.1.1 数据采样

采样(Sampling)方法通过特定的对数据采样的方式（例如过采样、降采样和合成采样等）改变数据集的数据分布，使得数据集中不同类别的数据分布较为均衡，从而改善数据不平衡问题。可以通过交叉验证的方式对采样的效果进行评估。采样方法中的常见算法可以分为3类：

（1）随机采样算法：包括随机过采样(Oversampling)和随机降采样(Undersampling)等；

（2）合成采样算法：其中包括SMOTE，Border-line-SMOTE, ADASYN, SMOTE+Tomek, oss等；

（3）基于聚类的采样算法：例如CBO等。

随机过采样算法首先对数据集中的少数类样本做随机采样，然后将采样出的样本加入数据集，并多次重复以上流程，得到数据分布更加平衡的数据集。

随机降采样算法首先对数据集中的多数类样本做随机采样，然后将采样出的样本移出数据集，并多次重复以上流程，得到数据分布更加平衡的数据集。

随机过采样和随机降采样都可以平衡数据集样本类别分布，有利于缓解数据不平衡问题。但过采样会将数据集中的少数类样本重复多次，易导致模型出现过拟合；降采样则会去除数据集中部分样本，导致信息损失问题。

合成采样方法是对随机采样方法的改进，最经典的合成采样算法是NV Chawla等人在2002年提出的SMOTE(Synthetic Minority Oversampling Technique)算法，对该算法的描述下图所示。

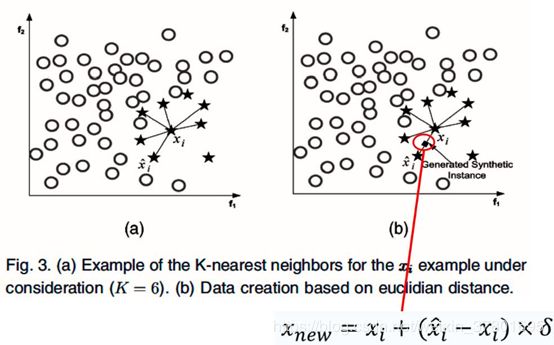
SMOTE算法是通过从少数类中随机选取2个样本，然后使用这2个样本作为基样本合成新的样本，一定程度上可以弥补随机过采样的缺陷，但在合成过程中可能会生成大量无效或者低价值样本。已经有很多基于SMOTE的改进算法，例如Border-line-SMOTE, ADASYN, SMOTE+Tomek, oss等。以Border-line-SMOTE为例，其算法描述如下图所示。

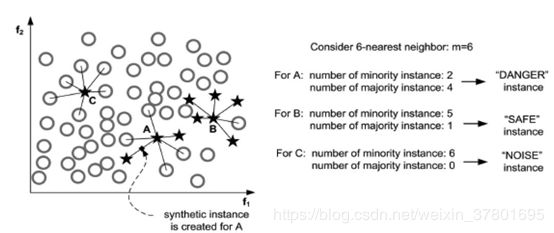
Border-line SMOTE对原始SMOTE算法的改进主要体现在对基样本的选择上，通过优先选择分类边界附近样本作为基样本的方法来提升合成样本的价值。

除了合成采样，还可以加入聚类的方法来改进随机采样算法，一种CBO(Cluster-based Oversampling)算法如下图所示。

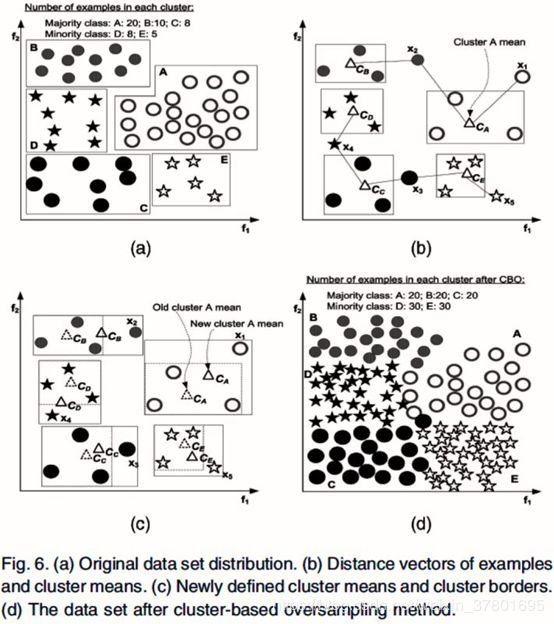
CBO算法流程主要包含以下3个步骤：
1）使用聚类算法分别对每个类别的样本做聚类，获得多个聚类cluster
2）对多数类的每个cluster做随机过采样或合成采样，使得每个cluster的样本数满足：表示多数类中最大cluster的样本数。
3）对少数类的每个cluster做随机过采样或合成采样，使得每个cluster的样本数满足：表示多数类在过采样之后的样本数，m_min为少数类聚类之后的聚类数目。

2.2 问题转化

2.2.1 转化为异常检测问题（一分类问题）

对于二分类问题，如果正负样本分布比例极不平衡，我们可以换一个完全不同的角度来看待问题：把它看做一分类（One Class Learning）或异常检测（Novelty Detection）问题。这类方法的重点不在于捕捉类间的差别，而是为其中一类进行建模，经典的工作包括One-class SVM等，如下图所示：

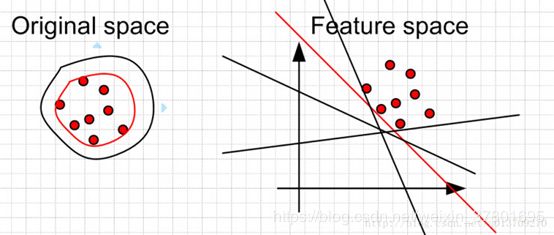
One Class SVM 是指你的训练数据只有一类正（或者负）样本的数据， 而没有另外的一类。在这时，你需要学习的实际上你训练数据的边界。而这时不能使用最大化软边缘了，因为你没有两类的数据。 所以假设最好的边缘要远离特征空间中的原点。左边是在原始空间中的边界，可以看到有很多的边界都符合要求，但是比较靠谱的是找一个比较紧的边界（红色的）。这个目标转换到特征空间就是找一个离原点比较远的边界，同样是红色的直线。当然这些约束条件都是人为加上去的，你可以按照你自己的需要采取相应的约束条件。比如让你data 的中心离原点最远。对于正负样本极不均匀的问题，使用异常检测，或者一分类问题，也是一个思路。

2.3 从模型上解决

2.3.1代价敏感型方法（调整模型训练目标函数）

代价敏感型(Cost-Sensitive)方法通过改变在模型训练过程中，不同类别样本分类错误时候的代价值来获得具有一定数据倾向性的分类模型。常见的代价敏感型方法有MetaCost, AdaCost, Adaptive Scaling等。

Adaptive Scaling

检测任务是信息抽取领域非常常见的任务，典型的任务如命名实体识别、关系抽取和事件检测等。在做检测任务时，我们可以把待检测的标签作为正例，其他标签作为反例，从而将检测任务转换为标准的分类任务。在这种分类任务中，一般使用交叉熵作为损失函数，正例的F值作为评价指标。由于正例（待检测的标签）往往非常稀疏，因此这是一个数据不平衡的分类任务。

最小化交叉熵损失等价于最大化Accuracy，而在计算Accuracy时，正负例的每个样本都是等价的。在计算F值时，正例和反例并非是等价的，这导致评估指标和优化目标出现了背离。因此在设计模型训练方法时，需要考虑到这种差异，尽量保证训练目标与评估指标的一致性。

Adaptive Scaling算法借鉴了经济学中的边际效用理论：指每新增（或减少）一个单位的商品或服务，它对商品或服务的收益增加（或减少）的效用。在分类任务中，将边际效用理论中的“商品或服务”替换为分类样本，收益即为评估指标（F值），此时的边际效用定义为：每新增（或减少）一个分类正确（错误）的样本，它对评估指标F值增加（或减少）的效用。由此，可以使用每个类别对F值的边际效用作为其重要程度的衡量。

实际计算时，可以将评估指标对TP和TN的偏导值作为正例和反例的边际效用值。如果是把Accuracy作为目标，计算正例和反例的边际效用可以得到：
可以看到，当把Accuracy作为目标时，正例和反例的边际效用始终是恒定而且相等的，如果是将F值作为目标，可以得到：

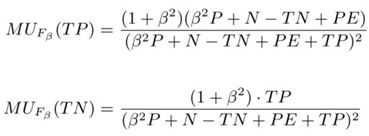
正例和反例的边际效用不再相等，而且在训练过程中会随着模型分类能力的变化而动态变化。调整之后的交叉熵损失：

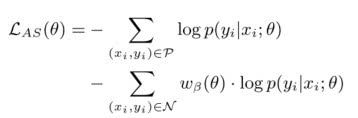
这样就得到了能够自动在训练过程中调整样本权重的Adaptive Scaling算法，而且该算法不需要引入任何额外的超参数。相比于传统的cost-sensitive方法，其特点在于：
1）正例和反例的相对重要程度既与正反例的比例有关，也会受到当前模型的分类能力影响
2）反例的重要性会随着正例分类准确率的提升而增加
3）反例的重要性也会随着反例分类准确率的提升而增加
4）当precision比recall更重要时，反例的重要性也会增加

2.3.2 集成学习方法

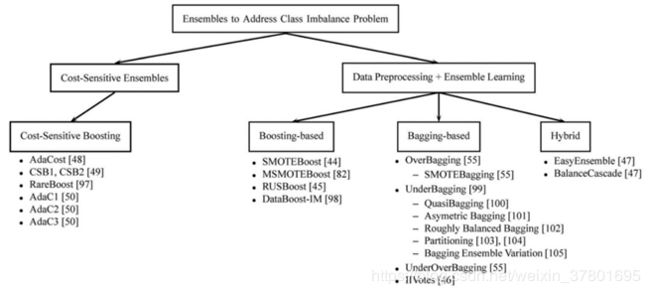
集成学习（Ensemble）是一种通过多分类器融合来获取更强分类性能的方法，将上两小节所述采样方法和代价敏感方法与之结合可以获得多种基于集成学习的数据不平衡下的学习算法，按照集成学习方法的不同，可以分为以下三类：

1）基于Bagging的方法。主要思想是将采样方法应用到Bagging算法的抽样过程中，具体操作时一般是首先从不均衡数据中抽取多个均衡子数据集，分别训练多个分类器，然后做Bagging模型集成。主要算法包括OverBagging, UnderBagging, UnderOverBagging, IIVotes等。

2）基于Boosting的方法。主要思想是将Boosting方法与采样方法或代价敏感型方法结合使用，因此又可以分为2小类：
a）代价敏感+Boosting: Boosting过程中更改类别权重，迭代时更关注少数类样本。主要算法包括AdaCost, CSB1, CSB2, RareBoost, AdaC1等。
b）采样方法+Boosting: Boosting过程中更改样本分布，迭代时更关注少数类样本。主要算法包括SMOTEBoost, MSMOTEBoost, RUSBoost, DataBoost-IM等。

3）Hybrid方法，即将基于Bagging的方法和基于Boosting的方法结合使用，主要算法包括EsayEnsemble和BalanceCascade等。

2.3.3 选择适用于不平衡数据的算法

某些算法支持不平衡样本处理，可以通过参数进行配置

参考链接
https://cloud.tencent.com/developer/news/300118
https://cloud.tencent.com/developer/news/302617
https://www.cnblogs.com/DjangoBlog/p/7903619.html
https://www.leiphone.com/news/201706/dTRE5ow9qBVLkZSY.html