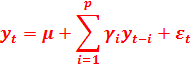时间序列ARIMA模型
时间序列ARIMA模型（预测模型）
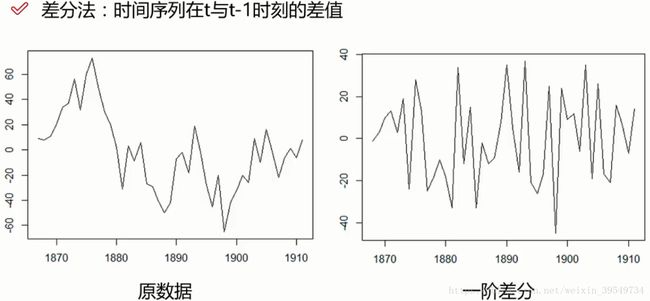
1.数据平稳性与差分法
A.平稳性
平稳性就是要求经样本时间序列所得到的拟合曲线在未来一段期间内仍能顺着现有的形态“惯性”地延续下去；
平稳性要求样本时间序列的均值和方差不发生明显变化
严平稳：严平稳表示的分布不随时间的改变而改变。只有当时间序列的所有统计性质都不会随着时间的推移而发生变化时,该序列才能被认为平稳。如：白噪声（正态），无论怎么取，都是期望为0，方差为1
弱平稳（宽平稳）：期望与相关系数（依赖性）不变，未来某时刻t的值Xt要依赖于它过去的信息，所以需要依赖性。实际数据大部分都是弱平稳。
B.差分法
问题：如果样本时间序列浮动特别大怎么办？怎么样处理这些数据来保证序列的平稳性呢？
--采用差分法：时间序列在t与 t-1时刻的差值
注意：二阶差分是在一阶差分的基础上再进行差分
应用：股票预测、降雨量预测
2.ARIMA模型
A.自回归模型AR（p阶）
自回归模型由于数据是时间序列，不存在变量与变量之间的关系，只有当前值与历史值之间的关系
--描述当前值与历史值之间的关系，用变量自身的历史时间数据对自身进行预测
--自回归模型必须满足平稳性的要求
--p阶（时间间隔）自回归过程的公式定义如下
--
：当前值；μ ：常数项；εt
：误差项；
--
：阶数（评估方法：PACF函数图）；
--
：自相关系数（求解方法：最大似然估计、最小二乘法）；
--
：表示当前值与前p阶都有关，是一个累加和的操作
自回归模型的限制
--自回归模型是用自身的数据来进行预测（训练数据集与测试集一样）
--必须具有平稳性
--必须具有自相关性，如果自相关系数（φi
）小于0.5，则不宜采用
--自回归只适用于预测与自身前期相关的现象
B.移动平均模型MA（q阶）
--移动平均模型关注的是自回归模型中的误差项的累加
--q阶自回归过程的公式定义如下：
--
：当前值；μ
：常数项；εt
：误差项；
--
：阶数（评估方法：ACF函数图）；
--
：误差项系数
--
：表示对误差项累加和的操作
--移动平均法能够有效地消除预测中的随机波动
C.自回归移动平均模型ARMA
--自回归AR与移动平均MA的结合
--公式定义如下：
D.差分自回归移动平均模型ARIMA
ARIMA(Autoregressive Integrated Moving Average Model)模型全称为自回归积分滑动平均模型，是由博克思(Box)和詹金斯(Jenkins)于70年代初提出一著名时间序列预测方法，所以又称为box-jenkins模型、博克思-詹金斯法。
其中ARIMA（p，d，q）称为差分自回归移动平均模型
--AR是自回归， p为自回归项数；
--MA为移动平均，q为移动平均项数；
--d为时间序列成为平稳时所做的差分次数。
ARIMA模型原理：将非平稳时间序列转化为平稳时间序列，仅对它的滞后值
以及随机误差项的现值
和滞后值
进行回归所建立的模型。ARIMA模型根据原序列是否平稳以及回归中所含部分的不同，包括自回归过程（AR）、移动平均过程（MA）、自回归移动平均过程（ARMA）以及差分自回归移动平均模型（ARIMA）过程。
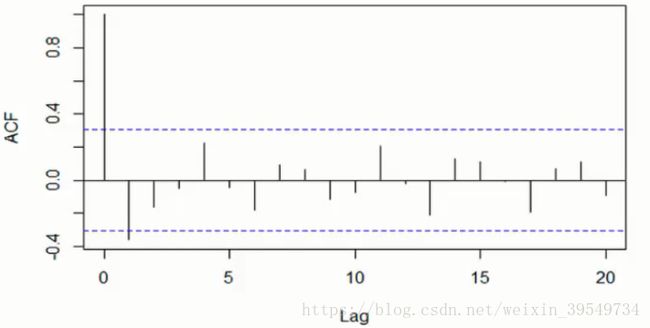
3.自相关函数ACF与偏自相关函数PACF
A.自相关函数ACF（用来确定q值）autocorrelation function
有序的随机变量序列与其自身相比较，自相关函数反映了同一序列在不同时序的取值之间的相关性
取值范围：[-1,1]
-1：负相关
+1：正相关
0：无关
虚线：置信区间
横轴：阶数
纵轴：ACF值
B.偏自相关函数PACF（用来确定p值）
--对于一个平稳的AR(p)模型，求出滞后k自相关系数p(k)时，实际上得到并不是x(t)与x(t-k)之间单纯的相关关系。
--x(t)同时还会受到中间k-1个随机变量x(t-1)、x(t-2)、……x(t-k+1)的影响，而这k-1个随机变量又都和x(t-k)具有相关关系，所以自相关系数p(k)里实际掺杂了其他变量对x(t)与x(t-k)的影响
--PACF剔除了中间k-1个随机变量x(t-1)、x(t-2)、……x(t-k+1)的干扰之后， x(t-k)对x(t) 单纯影响的相关程度
--ACF还包含了其他变量的影响，而PACF是严格这两个变量之间的相关性
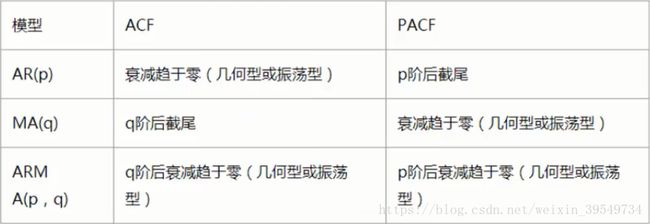
4.ARIMA（p,d,q）阶数确定
截尾：落在置信区间内（95%的点都符合规则）
AR(p)看PACF
MA(q)看ACF
5.建立ARIMA模型流程
A.将序列平稳（差分法确定d）
B.p和q阶数确定：结合图ACF和图PACF
C.ARIMA(p,d,q)
6.模型评估选择（目的：选择更简单的模型）
当有多组备选参数可以选择时，这时候就要根据AIC和BIC值进行模型参数的选择，通过衡量模型的复杂度来选择更简单的模型
A. AIC：赤池信息准则（普及一下：赤池是一个人名）
B. BIC：贝叶斯信息准则
k：模型参数个数
n：样本数量
L：最大似然函数
AIC和BIC值越低越好，其值越低，模型越简单，即k、n取值越小，L取值越大，模型越简单
7.模型残差检验（诊断残差序列是否为白噪声）
ARIMA模型的残差是否是期望为0且方差为常数的正态分布
QQ图：线性即正态分布
statsmodels库
8.ARIMA模型预测的基本程序
A.对原始序列的平稳性进行识别：根据时间序列的散点图、自相关函数图、偏自相关函数图以ADF单位根检验其方差、趋势及其季节性变化规律，一般来讲，经济运行的时间序列都不是平稳序列。
B.对非平稳序列进行平稳化处理：如果数据序列是非平稳的，并存在一定的增长或下降趋势，则需要对数据进行差分处理；如果数据存在异方差，则需对数据进行技术处理，直到处理后的数据的自相关函数值和偏相关函数值无显著地异于零。
C.根据时间序列模型的识别规则，建立相应的模型。
若平稳序列的偏相关函数是截尾的，而自相关函数是拖尾的，可断定序列适合AR模型；
若平稳序列的偏相关函数是拖尾的，而自相关函数是截尾的，则可断定序列适合MA模型；
若平稳序列的偏相关函数和自相关函数均是拖尾的，则序列适合ARMA模型。
截尾：指时间序列的自相关函数（ACF）或偏自相关函数（PACF）在某阶后均为0的性质（比如AR的PACF）
拖尾：ACF或PACF并不在某阶后均为0的性质（比如AR的ACF）
D.进行参数估计，检验是否具有统计意义。
E.进行假设检验，诊断残差序列是否为白噪声。
F. 利用已通过检验的模型进行预测分析。
更多AI资源请关注公众号：大胡子的AI
欢迎各位AI爱好者加入群聊交流学习：882345565（内有大量免费资源哦！）
版权声明：本文为博主原创文章，未经博主允许不得转载。如要转载请与本人联系。