图的无权最短路径算法
无权最短路径
- 对于无权图G(边没有权值或认为权值为1),如果G是连通的,则每个顶点之间都存在路径。
- 最短路径算法就是要找到一条连接不同顶点的最短路径。
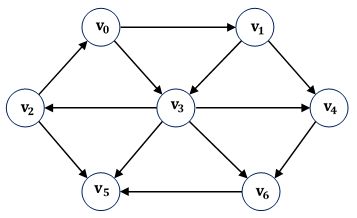
- 上图表示一个有向无权图,顶点 v2 v 2 到 V6 V 6 之间存在多条路径如 v2→v0→v1→v4→v6 v 2 → v 0 → v 1 → v 4 → v 6 为其中的1条,而最短的一条路径为 v2→v0→v3→v6 v 2 → v 0 → v 3 → v 6 。
无权最短路径算法
- 求顶点间的最短路径,首先可以遍历所有可能的路径,这种做法时间复杂度高。
- 另外,可以采取广度优先搜索的策略求顶点间的最短路径。具体过程如下:
- 一些必要准备:
- (1) 选取一个点s,例如上图的 v2 v 2 。我们求 v2 v 2 到所有其他顶点的最短路径。
- (2) 借助一个标记每个顶点状态的信息表InfoTable,包含三个必要的信息:是否被遍历Known,与 v2 v 2 的距离dist,以及标记上一个经过的顶点的Path。下图为求 v2 v 2 的最短路径的状态表的初始化。Known=0表示没被遍历,dist无穷大表示初始其他顶点都不可达。

- 对于下图求 v2 v 2 到其他顶点的最短路径
主要步骤- (1) 标记 v2 v 2 的Known为1,找与 v2 v 2 最近的点即遍历 v2 v 2 的邻接表,更新邻接表中的顶点 v0、v5 v 0 、 v 5 的Known=1,dist=0+1=1,Path= v2 v 2 。
- (2) 接着找离 v0 v 0 和 v5 v 5 的最近的点,对于 v0 v 0 ,遍历其邻接表,更新 v1 v 1 和 v3 v 3 的相关状态。
- (3) 最终得到一个状态表,从改状态表中可以提取 v2 v 2 到其他所有顶点的最短路径。
- (4) 该方法的时间复杂度为 O(|V|2) O ( | V | 2 ) ,主要细节在代码中描述:
template<class T>
void Graph::UnweightPath(int index) // 求图中某个顶点的无权最短路径
{
if (index >= size)
cout << "Out of range";
int Currdist; // 表示遍历过程中每一次的到index顶点的距离
for (Currdist = 0;Currdist < size;Currdist++) // 每次通过Currdist来指示接下来要处理的顶点及其邻接表
{
for (int i = 0;i < size;i++) // 遍历index顶点状态信息表
{
if (VSet[index].table[i].Known == false && VSet[index].table[i].dist == Currdist) // 如果某个顶点没被经过,且dist为当前距离值
{
VSet[index].table[i].Known = true; // 改变其状态
for (vector 无权最短路径算法2(借助队列)
主要步骤:
- 首先将目标顶点 v2 v 2 入队列。
- 当队列不为空时,执行循环:
- 顶点出队列,标记信息表中该顶点的状态Known=1(这个可以省去不要)。遍历该顶点的邻接表,当该顶点的邻接点的dist为无穷大时,更新它们的dist值为该顶点的dist+1,更新它们的Path值为该顶点。它们(该顶点的邻接点)入队列。
- 当队列为空时,遍历完 v2 v 2 的所有可达顶点。关于 v2 v 2 的状态表也更新完毕。读取状态表的Path栏,可以得到到所有顶点的最短路径。
- 借助队列的无权最短路径算法的时间复杂度为 O(|V|+|E|) O ( | V | + | E | ) 。
template<class T>
void Graph::UnweightPathQ(int index)
{
queue W;
Q.push(VSet[index]); // 下标为index的顶点入队列
while (!Q.empty()) // 当队列不为空
{
W = Q.front(); // 取队首元素
Q.pop(); // 出队
VSet[index].table[W.value].Known = true; // 该句可以省略
for (vector 附图的无权最短路径算法实现C++
- 上面可以看出,无论是算法1还是借助队列的算法2,求某个顶点到其他顶点的无权最短路径的过程,就是更新与之相关的状态信息表的过程。
- 故创建一个状态信息表类,顶点类包含一个状态信息表的成员。
#include* table; // 最短路径时每个顶点的信息栏
Vertex(T value = 0) :value(value) {}
};
template<class T>
class Graph{ // 创建一个图类
public:
vector &G) { size = G.size;VSet = G.VSet; } // 复制构造函数
void UnweightPath(int index); // 无权最短路径
void InitInfoTable(); // 初始化图中顶点的状态信息表
void PrintPath(int index); // 打印某个节点的最短路径
void UnweightPathQ(int index); // 借助队列的指定下标顶点的无权最短路径
private:
int size; // 图中顶点的个数
};
template<class T>
void Graph::InitInfoTable() // 初始化图中每个顶点的状态信息表
{
for (int i = 0;i < size;i++)
{
VSet[i].table = new InfoTable[size]; // 为每个顶点的状态表申请空间
for (int j = 0;j < size;j++)
{
VSet[i].table[j].Known = false; // 每个节点都没被经过
VSet[i].table[j].dist = INF; // 初始时每个顶点距离为无穷,表示不可达
VSet[i].table[j].Path = -1; // 初始Path为-1,方便以后遍历
}
VSet[i].table[i].dist = 0; // 初始时每个顶点距离自身为0
}
}
template<class T>
void Graph::UnweightPath(int index) // 求图中某个顶点的无权最短路径
{
if (index >= size)
cout << "Out of range";
int Currdist; // 表示遍历过程中每一次的到index顶点的距离
for (Currdist = 0;Currdist < size;Currdist++)
{
for (int i = 0;i < size;i++) // 遍历该顶点的状态表
{
if (VSet[index].table[i].Known == false && VSet[index].table[i].dist == Currdist) // 如果某个顶点没被经过,且dist为当前距离值
{
VSet[index].table[i].Known = true; // 改变其状态
for (vector::UnweightPathQ(int index)
{
queue W;
Q.push(VSet[index]); // 下标为index的顶点入队列
while (!Q.empty()) // 当队列不为空
{
W = Q.front(); // 取队首元素
Q.pop(); // 出队
VSet[index].table[W.value].Known = true; // 该句可以省略
for (vector::PrintPath(int index)
{
cout << "The InfoTable of V" << index << " is:\n";
for (int i = 0;i < size;i++) // 打印下标为index的顶点的状态表
{
cout<<"V"<" "<" " << VSet[index].table[i].dist
<< " "<<"V"<< VSet[index].table[i].Path << endl;
}
cout << "\nShow the unweighted paths form V"<< index << " to other vertices: \n";
stack - 运行结果
The InfoTable of V2 is:
V0 1 1 V2
V1 1 2 V0
V2 1 0 V-1
V3 1 2 V0
V4 1 3 V1
V5 1 1 V2
V6 1 3 V3
Show the unweighted paths form V2 to other vertices:
->V2->V0
->V2->V0->V1
->V2
->V2->V0->V3
->V2->V0->V1->V4
->V2->V5
->V2->V0->V3->V6
The InfoTable of V0 is:
V0 1 0 V-1
V1 1 1 V0
V2 1 2 V3
V3 1 1 V0
V4 1 2 V1
V5 1 2 V3
V6 1 2 V3
Show the unweighted paths form V0 to other vertices:
->V0
->V0->V1
->V0->V3->V2
->V0->V3
->V0->V1->V4
->V0->V3->V5
->V0->V3->V6
请按任意键继续. . .参考资料
Mark Allen Weiss: 数据结构与算法分析