机器学习算法——KNN算法总结

相关的资源的在我的github仓库中：https://github.com/2462612540/ML_Algorithm

KNN算法的简介：

KNN算法简称的为K近邻的算法。属于监督学习算法。其指导思想是”近朱者赤，近墨者黑“，即由你的邻居来推断出你的类别。KNN最邻近分类算法的实现原理：为了判断未知样本的类别，以所有已知类别的样本作为参照，计算未知样本与所有已知样本的距离，从中选取与未知样本距离最近的K个已知样本，根据少数服从多数的投票法则（majority-voting），将未知样本与K个最邻近样本中所属类别占比较多的归为一类。以上就是KNN算法在分类任务中的基本原理，实际上K这个字母的含义就是要选取的最邻近样本实例的个数。

中心思想：找到未分类的测试的样本附近的K个最相近的已经分类的样本，该样本的分类，由附近已经分类的样本的投票决定。

K值的选择：

    K值选的太大易引起欠拟合，太小容易过拟合，需交叉验证确定K值。

    通常是根据先验知识来选择K的值、通常也是选择是奇数、一般选择是(1,n] 其中n为样本的总数。

算法的流程说明：

 

K-D树的讲解：

    KD树算法没有一开始就尝试对测试样本分类，而是先对训练集建模，建立的模型就是KD树，建好了模型再对测试集做预测。所谓的KD树就是K个特征维度的树，注意这里的K和KNN中的K的意思不同。KNN中的K代表特征输出类别，KD树中的K代表样本特征的维数。为了防止混淆，后面我们称特征维数为n。

KD树算法包括三步，第一步是建树，第二部是搜索最近邻，最后一步是预测。

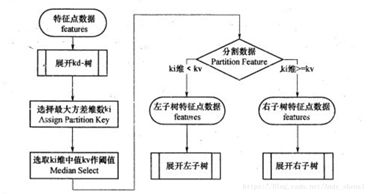
1、KD树的建立

我们首先来看建树的方法。KD树建树采用的是从m个样本的n维特征中，分别计算n个特征的取值的方差，用方差最大的第k维特征nk来作为根节点。对于这个特征，我们选择特征nk的取值的中位数nkv对应的样本作为划分点，对于所有第k维特征的取值小于nkv的样本，我们划入左子树，对于第k维特征的取值大于等于nkv的样本，我们划入右子树，对于左子树和右子树，我们采用和刚才同样的办法来找方差最大的特征来做更节点，递归的生成KD树。

构造平衡kd树算法：

输入:k维空间数据集T={x1,x2,…,xN},其中xi=(x(1)i,x(2)i,…,x(k)i)T, i=1,2,…N;输出:kd树

(1)开始：构造根结点，根结点对应于包含T

的k维空间的超矩形区域。

选择x(1)为坐标轴，以T中所有实例的x(1)坐标的中位数为切分点，将根结点对应的超矩形区域切分为两个子区域。切分由通过切分点并与坐标轴x(1)垂直的超平面实现。 将落在切分超平面上的实例点保存在根结点。

(2)重复。对深度为j的结点，选择x(l)为切分的坐标轴，l=j(modk)+1，以该结点的区域中所有实例的x(l)

坐标的中位数为切分点，将该结点对应的超矩形区域切分为两个子区域。切分由通过切分点并与坐标轴x(l)垂直的超平面实现。 由该结点生成深度为j+1的左、右子结点：左子结点对应坐标x(l)小于切分点的子区域，右子结点对应坐标x(l)大于切分点的子区域。 将落在切分超平面上的实例点保存在该结点。

(3)直到两个子区域没有实例存在时停止,从而形成kd 树的区域划分.

 

有了KD树搜索最近邻的办法，KD树的预测就很简单了，在KD树搜索最近邻的基础上，我们选择到了第一个最近邻样本，就把它置为已选。在第二轮中，我们忽略置为已选的样本，重新选择最近邻，这样跑k次，就得到了目标的K个最近邻，然后根据多数表决法，如果是KNN分类，预测为K个最近邻里面有最多类别数的类别。如果是KNN回归，用K个最近邻样本输出的平均值作为回归预测值。

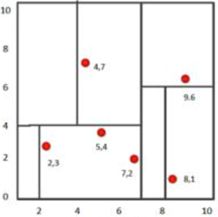
比如我们有二维样本6个，{(2,3)，(5,4)，(9,6)，(4,7)，(8,1)，(7,2)}，构建kd树的具体步骤为：

1、 确定：split域=x。具体是：6个数据点在x，y维度上的数据方差分别为39，28.63，所以在x轴上方差更大，故split域值为x；

2、确定：Node-data =（7,2）。具体是：根据x维上的值将数据排序，6个数据的中值(所谓中值，即中间大小的值)为7[这里中位数应该是(5+7)/2=6,但是参考了所有的资料–李航的统计学习方法–都是按照7来的，所以我这里也按照7来进行分区]，所以Node-data域位数据点（7,2）。这样，该节点的分割超平面就是通过（7,2）并垂直于：split=x轴的直线x=7；

3、确定：左子空间和右子空间。具体是：分割超平面x=7将整个空间分为两部分：x<=7的部分为左子空间，包含3个节点={(2,3),(5,4),(4,7)}；另一部分为右子空间，包含2个节点={(9,6)，(8,1)}；

4、用同样的办法划分左子树的节点{(2,3),(5,4),(4,7)}和右子树的节点{(9,6)，(8,1)}。最终得到KD树。

算法的优缺点的总结

KNN算法的优点：

1） 理论成熟，思想简单，既可以用来做分类也可以用来做回归

2） 可用于非线性分类

3） 训练时间复杂度比支持向量机之类的算法低，仅为O(n)

4） 朴素贝叶斯之类的算法比，对数据没有假设，准确度高，对异常点不敏感

5） 由于KNN方法主要靠周围有限的邻近的样本，而不是靠判别类域的方法来确定所属类别的，因此对于类域的交叉或重叠较多的待分样本集来说，KNN方法较其他方法更为适合

6）该算法比较适用于样本容量比较大的类域的自动分类，而那些样本容量较小的类域采用这种算法比较容易产生误分。

KNN算法的缺点：

1）计算量大，尤其是特征数非常多的时候

2）样本不平衡的时候，对稀有类别的预测准确率低

3）KD树，球树之类的模型建立需要大量的内存

4）使用懒散学习方法，基本上不学习，导致预测时速度比起逻辑回归之类的算法慢

5）相比决策树模型，KNN模型可解释性不强

#!/usr/bin/env python
# -*- coding: utf-8 -*-
# @Time    : 12/13/2019 3:35 PM
# @Author  : xjl
# @File    : cancer_knn.py
# @Software: PyCharm

import csv
import random

data_path="you file path"
k=1

# 读取数据
with open(data_path,'r') as file:
    reader=csv.DictReader(file)
    datas=[row for row in reader]
    # print("row=",format(data))

# 数据的分组
n=len(datas)//3
random.shuffle(datas)
test_set=datas[0:n]
train_set=datas[n:]
# print("train_set=",train_set)
# print("test_set",test_set)

#距离的选择
def distance(d1,d2):
    res=0
    for key in ("radius","texture","perimeter","area","smoothness","compactness","symmetry","fractal_dimension"):
        res+=(float(d1[key])-float(d2[key]))**2
    return res**0.5

#KNN的算法
"""data 这个是求解的数据，包括这个数据的所有的特征的数据"""
def KNN(data):
    #求距离
    res=[{"result":train['diagnosis_result'],"distance":distance(data,train)} for train in train_set]
    #进行排序
    sorted(res,key=lambda item:item['distance'])
    # print("res=", res)
    #取前面的K个
    res2=res[0:k]
    # print(res2)
    #来一个加权的平均的数
    result={'B':0,'M':0}
    #求解总的距离
    total_length=0
    for r in res2:
        total_length+=r['distance']
    for r in res2:
        result[r['result']]+=1-r['distance']/total_length#这里的是要么是B 或者是M  =单个的距离/总的距离

    if result['B']>result['M']:
        return 'B'
    else:
        return 'M'

#测试的阶段
correct=0
for test in test_set:
    result=test['diagnosis_result']
    result2=KNN(test)
    if result==result2:
        correct+=1;

print(correct)
print(len(test_set))
print("准确率=",correct/len(test_set))