VINS-Mono关键知识点总结——预积分和后端优化IMU部分

VINS-Mono关键知识点总结——预积分和后端优化IMU部分

像VINS-Mono这样优秀的框架网上优秀的总结实在太多，我写这篇博客仅仅是为了自己将知识点梳理得更加清楚写的，也顺带分享出来和大家交流，先推荐几篇大佬的总结：
VINS技术路线与代码详解
VINS-Mono论文学习与代码解读——目录与参考
VINS-Mono详解.pdf
VINS-mono详细解读
VINS论文推导及代码解析 by 崔华坤
大家大都是相互借阅补充，以我的水平现在也只能是看了别人的总结自己的，不过也多亏了有这么多善意的分享才能这么快地对一个框架能有所了解，不废话了，进入正题

首先为什么要将预积分和后端优化放在一起写呢？这两个其实是很独立的知识点，因为我觉得这两者可以组成其中一条很重要的pipeline，通过这个把这条pipeline理清了就能更好地理解为什么要做预积分以及Vins-Mono的后端有什么不同，当然，预积分的结果不仅仅是给后端优化用的，下面从预积分开始总结。

1. 预积分的理论推导

第一个问题是为什么要预积分呢？
首先积分是肯定需要的，因为IMU的频率通常是远高于Camera的，而IMU获得的是每一时刻的加速度和角速度，我们通过积分获得两帧之间的由IMU测出的位移和旋转变换。那么预积分呢？在世界坐标系下的连续时刻积分是这样计算的：$$p_{b_{k+1}}^w=p_{b_k}^w+v_{b_k}^w\Delta t_k+{\iint }_{t\in [k,k+1]}\left[R_t^w\left({\hat{a}}_t-b_{a_t}\right)-g^w\right]d{t}^2$$$$v_{b_{k+1}}^w=v_{b_k}^w+{\int }_{t\in [k,k+1]}\left[R_t^w\left({\hat{a}}_t-b_{a_t}\right)-g^w\right]dt\text{\hspace{1em}(1)}$$$$q_{b_{k+1}}^w=q_{b_k}^w\otimes {\int }_{t\in [k,k+1]2}\Omega \left({\omega }_t-b_{{\omega }_t}\right)q_t^{b_k}dt$$其中$$\Omega (w)=\left[\begin{array}{cc}-[w{]}_{\times }& w\\ -w^T& 0\end{array}\right],[w{]}_{\times }=\left[\begin{array}{ccc}0& -w_z& w_y\\ w_z& 0& -w_x\\ -w_y& w_x& 0\end{array}\right]$$因为我们获得的IMU数据是离散的，所以第一步我们先需要对上述（1）式进行离散化：$$p_{b_{i+1}}^w=p_{b_i}^w+v_{b_i}^w\delta t+\frac{1}{2}{\overline{\hat{a}}}_i\delta t^2$$$$v_{b_{i+1}}^w=v_{b_i}^w+{\overline{\hat{a}}}_i\delta t\text{\hspace{1em}(2)}$$$$q_{b_{i+1}}^w=q_{b_i}^w\otimes \left[\begin{array}{c}1\\ \frac{1}{2}{\omega }_i\delta t\end{array}\right]$$
其中，运用了中值积分有$${\overline{\hat{a}}}_i=\frac{1}{2}\left[q_i\left({\hat{a}}_i-b_{a_i}\right)-g^w+q_{i+1}\left({\hat{a}}_{i+1}-b_{a_i}\right)-g^w\right]$$$${\overline{\hat{\omega }}}_i=\frac{1}{2}\left({\omega }_i+{\omega }_{i+1}\right)-b_{{\omega }_i}$$

这样会遇到一个问题就是假如我们通过后端优化使得$p_{b_k}^w$和$v_{b_k}^w$等发生了变化，那么$p_{b_{k+1}}^w$我们就需要重新按照上述公式积分一次，如下图所示

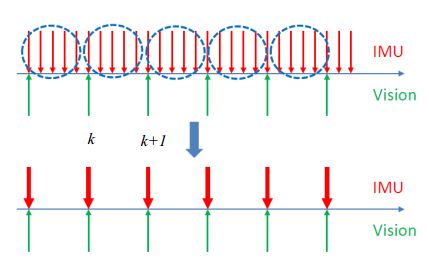
这里需要先剧透下我们的后端优化里面的代价函数是包括两帧之间的残差量，以位置为例，就是状态量$p_{b_k}^w$和$p_{b_{k+1}}^w$以及IMU积分出来的结果之间的差，如果我们想获得这个位置差，我们如果按照（2）式计算，我们需要计算上图第一幅图中红色箭头的每一个位置的状态量，这是我们不愿意发生的，因此我们引入了预积分，它的作用就是避免重复积分，将IMU预积分的参考坐标系改为前一帧体坐标系，从而获得两帧之间的相对运动，也就是第二幅图中红色箭头之间的量。

下面就按照正常的推导走一遍，然后我最后会对应着代码解释推导的结果：
既然我们要避免第$b_k$帧的影响，我们就需要以$b_k$帧为参考系，如下：$$R_w^{b_k}{p}_{b_{k+1}}^w=R_w^{b_k}\left(p_{b_k}^w+v_{b_k}^w\Delta t_k-\frac{1}{2}{g}^w\Delta t_k^2\right)+{\alpha }_{b_{k+1}}^{b_k}$$$$R_w^{b_k}{v}_{b_{k+1}}^w=R_w^{b_k}\left(v_{b_k}^w-g^w\Delta t_k\right)+{\beta }_{b_{k+1}}^{b_k}\text{\hspace{1em}(3)}$$$$q_w^{b_k}\otimes q_{b_{k+1}}^w={\gamma }_{b_{k+1}}^{b_k}$$其中$${\alpha }_{b_{k+1}}^{b_k}={\iint }_{t\in [k,k+1]}\left[R_t^{b_k}\left({\hat{a}}_t-b_{a_t}\right)\right]d{t}^2$$$${\beta }_{b_{k+1}}^{b_k}={\int }_{t\in [k,k+1]}\left[R_t^{b_k}\left({\hat{a}}_t-b_{a_t}\right)\right]dt\text{\hspace{1em}(4)}$$$${\gamma }_{b_{k+1}}^{b_k}={\int }_{t\in [k,k+1]}\frac{1}{2}\Omega \left({\hat{\omega }}_t-b_{{\omega }_t}\right){\gamma }_t^{b_k}dt$$上述（4）式就是我们需要的预积分公式了，但是它是连续形式下的，因此我们将其离散化：$${\hat{\alpha }}_{i+1}^{b_k}={\hat{\alpha }}_i^{b_k}+{\hat{\beta }}_i^{b_k}\delta t+\frac{1}{2}{\overline{\hat{a}}}_i^{\prime }\delta t^2$$$${\hat{\beta }}_{i+1}^{b_k}={\hat{\beta }}_i^{b_k}+{\overline{\hat{a}}}_i^{\prime }\delta t\text{\hspace{1em}(5)}$$$${\hat{\gamma }}_{i+1}^{b_k}={\hat{\gamma }}_i^{b_k}\otimes {\hat{\gamma }}_{i+1}^i={\hat{\gamma }}_i^{b_k}\otimes \left[\begin{array}{c}1\\ \frac{1}{2}{\overline{\hat{\omega }}}_i^{\prime }\delta t\end{array}\right]$$其中$${\overline{\hat{a}}}_i^{\prime }=\frac{1}{2}\left[q_i\left({\hat{a}}_i-b_{a_i}\right)+q_{i+1}\left({\hat{a}}_{i+1}-b_{a_i}\right)\right]$$$${\overline{\hat{\omega }}}_i^{\prime }=\frac{1}{2}\left({\omega }_i+{\omega }_{i+1}\right)-b_{{\omega }_i}$$这里值得注意的是，以位置变化为例，(5)中的${\hat{\alpha }}_{i+1}^{b_k}$和(6)中的${\alpha }_{b_{k+1}}^{b_k}$并不是一回事，当然，下标不一样可以忽略，主要不一样的地方是(6)中的${\alpha }_{b_{k+1}}^{b_k}$计算是加速度计和陀螺仪的Bias是实时在变化的，而(5)中的${\hat{\alpha }}_{i+1}^{b_k}$计算时默认是不变的，在等下的源码里可以看出来积分计算时用的Bias固定是是$b_k$帧时的，而不是实时变化的，因此会存在一个和Bias相关的误差如下：$${\alpha }_{b_{k+1}}^{b_k}\approx {\hat{\alpha }}_{b_{k+1}}^{b_k}+J_{b_a}^{\alpha }\delta b_a+J_{b_{\omega }}^{\alpha }\delta b_{\omega }$$$${\beta }_{b_{k+1}}^{b_k}\approx {\hat{\beta }}_{b_{k+1}}^{b_k}+J_{b_a}^{\beta }\delta b_a+J_{b_{\omega }}^{\beta }\delta b_{\omega }\text{\hspace{1em}(6)}$$$${\gamma }_{b_{k+1}}^{b_k}\approx {\hat{\gamma }}_{b_{k+1}}^{b_k}\otimes \left[\begin{array}{c}1\\ \frac{1}{2}{J}_{b_{\omega }}^{\gamma }\delta b_{\omega }\end{array}\right]$$
那么上式中的$J_{b_a}^{\alpha }$，$J_{b_{\omega }}^{\alpha }$，$J_{b_a}^{\beta }$，$J_{b_{\omega }}^{\beta }$怎么计算呢，接下来进一步推导

---------------------我是分割线----------------------下面就是怎么推导误差了------------------------

在上面的推导中引入误差的不仅仅是将变换的Bias视为不变，还存在加速度计和陀螺仪的噪声，同时位置、速度和角度之间的误差也会相互影响，并且误差是随时间一直累计的，因此，我们直接给出误差的状态方程，也就是误差变化的情况，通过误差的变化以及上一时刻累计的误差我们就可以求得下一时刻的误差：$$\begin{array}{rl}\left[\begin{array}{c}\delta {\dot{\alpha }}_t^{b_k}\\ \delta {\dot{\beta }}_t^{b_k}\\ \delta {\dot{\theta }}_t^{b_k}\\ \delta {\dot{b}}_{a_t}\\ \delta {\dot{b}}_{w_i}\end{array}\right]& =\left[\begin{array}{ccccc}0& I& 0& 0& 0\\ 0& 0& -{\hat{R}}_t^{b_k}{\left[a_t-{\hat{b}}_{a_i}\right]}_{\times }& -{\hat{R}}_t^{b_k}& 0\\ 0& 0& -{\left[w_t-{\hat{b}}_{w_i}\right]}_{\times }& 0& -I\\ 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0\end{array}\right]\left[\begin{array}{c}\delta {\alpha }_t^{b_k}\\ \delta {\beta }_t^{b_k}\\ \delta {\theta }_t^{b_k}\\ \delta b_{a_t}\\ \delta b_{w_i}\end{array}\right]+\left[\begin{array}{cccc}0& 0& 0& 0\\ -{\hat{R}}_t^{b_k}& 0& 0& 0\\ 0& -I& 0& 0\\ 0& 0& I& 0\\ 0& 0& 0& I\end{array}\right]\left[\begin{array}{c}{n}_a\\ n_w\\ n_{b_a}\\ n_{b_w}\end{array}\right]\\ & =F_t\delta z_t^{b_k}+G_t{n}_t\end{array}$$那么根据导数的定义有上一时刻推导下一时刻的误差如下：$$\delta z_{t+\delta t}^{b_k}=\delta z_t^{b_k}+\delta {\dot{z}}_t^{b_k}\delta t=\left(\mathrm{I}+F_t\delta t\right)\delta z_t^{b_k}+\left(G_t\delta t\right)n_t=F\delta z_t^{b_k}+V{n}_t\text{\hspace{1em}(7)}$$类比EKF的运动转移方程（其实也是把一个原本非线性的方程线性化），我们类似给出误差的协方差变化：
$$P_{t+\delta t}^{bk}=\left(1+F_t\delta t\right)P_t^{b_k}{\left(1+F_t\delta t\right)}^T+\left(G_t\delta t\right)Q{\left(G_t\delta t\right)}^T\text{\hspace{1em}(8)}$$因为上面的方程是线性方程，那么我们的状态转移方程关于$\delta z_t$的雅克比矩阵也可以递推出来：$$J_{t+\delta t}=\left(\mathrm{I}+F_t\delta t\right)J_t\text{\hspace{1em}(9)}$$上面的公式都是在连续时间推导的（t嘛）所以我们下面对应进行离散化一下：
(7)式离散形式为：$$\left[\begin{array}{c}\delta {\alpha }_{k+1}\\ \delta {\theta }_{k+1}\\ \delta {\beta }_{k+1}\\ \delta b_{a_{k+1}}\\ \delta b_{w+1}\end{array}\right]=\left[\begin{array}{ccccc}I& f_{01}& \delta t& f_{03}& f_{04}\\ 0& f_{11}& 0& 0& -\delta t\\ 0& f_{21}& I& f_{23}& f_{24}\\ 0& 0& 0& I& 0\\ 0& 0& 0& 0& I\end{array}\right]\left[\begin{array}{c}\delta {\alpha }_k\\ \delta {\theta }_k\\ \delta {\beta }_a\\ \delta b_{a_k}\\ \delta b_{w_k}\end{array}\right]+\left[\begin{array}{cccccc}{v}_{00}& v_{01}& v_{02}& v_{03}& 0& 0\\ 0& \frac{-\delta t}{2}& 0& \frac{-\delta t}{2}& 0& 0\\ -\frac{R_k\delta t}{2}& v_{21}& -\frac{R_{k+1}\delta t}{2}& v_{23}& 0& 0\\ 0& 0& 0& 0& \delta t& 0\\ 0& 0& 0& 0& 0& \delta t\end{array}\right]\left[\begin{array}{c}{n}_{a_k}\\ n_{w_k}\\ n_{a_{k+1}}\\ n_{w_{k+1}}\\ n_{b_a}\\ n_{b_w}\end{array}\right]$$其中$$\begin{array}{rl}& f_{01}=\frac{\delta t}{2}{f}_{21}=-\frac{1}{4}{R}_k{\left({\hat{a}}_k-b_{a_k}\right)}^{\wedge }\delta t^2-\frac{1}{4}{R}_{k+1}{\left({\hat{a}}_{k+1}-b_{a_k}\right)}^{\wedge }\left[I-{\left(\frac{{\omega }_k+{\omega }_{k+1}}{2}-b_{{\omega }_k}\right)}^{\wedge }\delta t\right]\delta t^2\\ & f_{03}=-\frac{1}{4}\left(R_k+R_{k+1}\right)\delta t^2\\ & f_{04}=\frac{\delta t}{2}{f}_{24}=\frac{1}{4}{R}_{k+1}{\left({\hat{a}}_{k+1}-b_{a_k}\right)}^{\wedge }\delta t^3\\ & f_{11}=I-{\left(\frac{{\omega }_k+{\omega }_{k+1}}{2}-b_{{\omega }_k}\right)}^{\wedge }\delta t\\ & f_{21}=-\frac{1}{2}{R}_k{\left({\hat{a}}_k-b_{a_k}\right)}^{\wedge }\delta t-\frac{1}{2}{R}_{k+1}{\left({\hat{a}}_{k+1}-b_{a_k}\right)}^{\wedge }\left[I-{\left(\frac{{\omega }_k+{\omega }_{k+1}}{2}-b_{{\omega }_k}\right)}^{\wedge }\delta t\right]\delta t\\ & f_{23}=-\frac{1}{2}\left(R_k+R_{k+1}\right)\delta t\\ & f_{24}=\frac{1}{2}{R}_{k+1}{\left({\hat{a}}_{k+1}-b_{a_k}\right)}^{\wedge }\delta t^2\\ & v_{00}=-\frac{1}{4}{R}_k\delta t^2\\ & v_{01}=v_{03}=\frac{\delta t}{2}{v}_{21}=\frac{1}{4}{R}_{k+1}{\left({\hat{a}}_{k+1}-b_{a_k}\right)}^{\wedge }\delta t^2\frac{\delta t}{2}\\ & v_{02}=-\frac{1}{4}{R}_{k+1}\delta t^2\\ & v_{21}=v_{23}=\frac{1}{4}{R}_{k+1}{\left({\hat{a}}_{k+1}-b_{a_k}\right)}^{\Lambda }\delta t^2\end{array}$$
可以简写为$$\delta z_{k+1}^{15\times 1}=F^{15\times 15}\delta z_k^{15\times 1}+V^{15\times 18}{Q}^{18\times 1}\text{\hspace{1em}(10)}$$

(8)式的离散形式如下：
$$P_{k+1}^{15\times 15}=F{P}_k{F}^T+VQ{V}^T\text{\hspace{1em}(11)}$$其中$$Q^{18\times 18}=\left[\begin{array}{cccccc}{\sigma }_a^2& 0& 0& 0& 0& 0\\ 0& {\sigma }_w^2& 0& 0& 0& 0\\ 0& 0& {\sigma }_a^2& 0& 0& 0\\ 0& 0& 0& {\sigma }_w^2& 0& 0\\ 0& 0& 0& 0& {\sigma }_{b_a}^2& 0\\ 0& 0& 0& 0& 0& {\sigma }_{b_w}^2\end{array}\right]$$

(9)式的离散形式如下：$$J_{k+1}^{15\times 15}=F{J}_k\text{\hspace{1em}(12)}$$上面我仅仅是给出了结果，从大流程上走了一遍（全部写一遍太费时间了），如果想知道这些公式是怎么给出的，可以参考VINS-Mono详解.pdf或者崔华坤老师的推导。

2. 预积分的代码分析

和预积分相关的代码主要在estimator_node.cpp、estimator.cpp和intergration_base.h中，三个文件中分别各有一段：
（1）在estimator_node.cpp中的pridict函数中

Eigen::Vector3d un_acc_0 = tmp_Q * (acc_0 - tmp_Ba) - estimator.g;
Eigen::Vector3d un_gyr = 0.5 * (gyr_0 + angular_velocity) - tmp_Bg;
tmp_Q = tmp_Q * Utility::deltaQ(un_gyr * dt);
Eigen::Vector3d un_acc_1 = tmp_Q * (linear_acceleration - tmp_Ba) - estimator.g;
Eigen::Vector3d un_acc = 0.5 * (un_acc_0 + un_acc_1);
tmp_P = tmp_P + dt * tmp_V + 0.5 * dt * dt * un_acc;
tmp_V = tmp_V + dt * un_acc;

这一段并不是预积分公式，只是和预积分相关的一部分，这一部分对应的是上面的公式（2），而且是在tmp_P、tmp_V、tmp_Q是在非线性优化之后获得的世界坐标系下准确的位置、速度和位姿。

（2）在estimator.cpp中的processIMU函数中

Vector3d un_acc_0 = Rs[j] * (acc_0 - Bas[j]) - g;
Vector3d un_gyr = 0.5 * (gyr_0 + angular_velocity) - Bgs[j];
Rs[j] *= Utility::deltaQ(un_gyr * dt).toRotationMatrix();
Vector3d un_acc_1 = Rs[j] * (linear_acceleration - Bas[j]) - g;
Vector3d un_acc = 0.5 * (un_acc_0 + un_acc_1);
Ps[j] += dt * Vs[j] + 0.5 * dt * dt * un_acc;
Vs[j] += dt * un_acc;

这里也是对应上面公式（2），但是这里的Ps[j]、 Vs[j]、Rs[j]是未经后端优化之前的位置、速度和位姿。

（3）在integration_base.h中的midPointIntegration函数中

Vector3d un_acc_0 = delta_q * (_acc_0 - linearized_ba);
Vector3d un_gyr = 0.5 * (_gyr_0 + _gyr_1) - linearized_bg;
result_delta_q = delta_q * Quaterniond(1, un_gyr(0) * _dt / 2, un_gyr(1) * _dt / 2, un_gyr(2) * _dt / 2);
Vector3d un_acc_1 = result_delta_q * (_acc_1 - linearized_ba);
Vector3d un_acc = 0.5 * (un_acc_0 + un_acc_1);
result_delta_p = delta_p + delta_v * _dt + 0.5 * un_acc * _dt * _dt;
result_delta_v = delta_v + un_acc * _dt;

这里对应上面的公式（5），这里的result_delta_p、result_delta_v和result_delta_q就是相对于$b_k$帧的预积分，对应预计分类IntergrationBase类中delta_p、delta_v、delta_q三个全局变量，每来一帧新图像或者滑动一次窗口时就会新创建一个预计分，创建时预积分中的delta_p、delta_v、delta_q中这三个量都设为零，然后在获得新的IMU值之后不断积分。
同样在midPointIntegration函数中，在上面预积分完成之后，马上会更新相关的雅克比矩阵和协方差矩阵：

MatrixXd F = MatrixXd::Zero(15, 15);//这里可以看出来F是一个15*15的矩阵
F.block<3, 3>(0, 0) = Matrix3d::Identity();
F.block<3, 3>(0, 3) = -0.25 * delta_q.toRotationMatrix() * R_a_0_x * _dt * _dt + 
                      -0.25 * result_delta_q.toRotationMatrix() * R_a_1_x * (Matrix3d::Identity() - R_w_x * _dt) * _dt * _dt;
F.block<3, 3>(0, 6) = MatrixXd::Identity(3,3) * _dt;
F.block<3, 3>(0, 9) = -0.25 * (delta_q.toRotationMatrix() + result_delta_q.toRotationMatrix()) * _dt * _dt;
F.block<3, 3>(0, 12) = -0.25 * result_delta_q.toRotationMatrix() * R_a_1_x * _dt * _dt * -_dt;
F.block<3, 3>(3, 3) = Matrix3d::Identity() - R_w_x * _dt;
F.block<3, 3>(3, 12) = -1.0 * MatrixXd::Identity(3,3) * _dt;
F.block<3, 3>(6, 3) = -0.5 * delta_q.toRotationMatrix() * R_a_0_x * _dt + 
                      -0.5 * result_delta_q.toRotationMatrix() * R_a_1_x * (Matrix3d::Identity() - R_w_x * _dt) * _dt;
F.block<3, 3>(6, 6) = Matrix3d::Identity();
F.block<3, 3>(6, 9) = -0.5 * (delta_q.toRotationMatrix() + result_delta_q.toRotationMatrix()) * _dt;
F.block<3, 3>(6, 12) = -0.5 * result_delta_q.toRotationMatrix() * R_a_1_x * _dt * -_dt;
F.block<3, 3>(9, 9) = Matrix3d::Identity();
F.block<3, 3>(12, 12) = Matrix3d::Identity();

MatrixXd V = MatrixXd::Zero(15,18);//V是一个15*18的矩阵
V.block<3, 3>(0, 0) =  0.25 * delta_q.toRotationMatrix() * _dt * _dt;
V.block<3, 3>(0, 3) =  0.25 * -result_delta_q.toRotationMatrix() * R_a_1_x  * _dt * _dt * 0.5 * _dt;
V.block<3, 3>(0, 6) =  0.25 * result_delta_q.toRotationMatrix() * _dt * _dt;
V.block<3, 3>(0, 9) =  V.block<3, 3>(0, 3);
V.block<3, 3>(3, 3) =  0.5 * MatrixXd::Identity(3,3) * _dt;
V.block<3, 3>(3, 9) =  0.5 * MatrixXd::Identity(3,3) * _dt;
V.block<3, 3>(6, 0) =  0.5 * delta_q.toRotationMatrix() * _dt;
V.block<3, 3>(6, 3) =  0.5 * -result_delta_q.toRotationMatrix() * R_a_1_x  * _dt * 0.5 * _dt;
V.block<3, 3>(6, 6) =  0.5 * result_delta_q.toRotationMatrix() * _dt;
V.block<3, 3>(6, 9) =  V.block<3, 3>(6, 3);
V.block<3, 3>(9, 12) = MatrixXd::Identity(3,3) * _dt;
V.block<3, 3>(12, 15) = MatrixXd::Identity(3,3) * _dt;

jacobian = F * jacobian;
covariance = F * covariance * F.transpose() + V * noise * V.transpose();

对应上述推导中的公式（11） 和 公式（12），但是并没有计算公式（10），这是应为，通过预积分误差的递推公式确实可以求出来从$b_k$帧到$b_{k+1}$帧的累积出来的误差大小，但是这个值并没有用，我们在后端需要的是误差对$b_k$帧和$b_{k+1}$帧的导数，而误差对$b_k$帧的导数却可以通过公式(12)的雅克比矩阵直接计算出来，至于协方差矩阵是我们进行后端优化计算残差时用马氏距离需要用到的，这里提到了那么多和后端有关的东西，现在就顺着来总结下后端优化相关的知识

3. 后端优化IMU部分

（1）残差定义

这里仅仅总结下和预积分先关的后端优化IMU部分，完整的后端优化等把Marginization搞明白之后再总结，IMU定义的残差是两帧之间的位置、速度、旋转以及Bias变换量的差（就是通过公式（2）积分出来的世界坐标系下$b_k$和$b_{k+1}$之间的变换和预积分所求的变换之间的差），如下：$$r_B^{15\times 1}\left({\hat{z}}_{b_{k+1}^{\prime }}^{b_k},X\right)=\left[\begin{array}{c}\delta {\alpha }_{b_{k+1}}^{b_k}\\ \delta {\theta }_{b_{k+1}}^{b_k}\\ \delta {\beta }_{b_{k+1}}^{b_k}\\ \delta b_a\\ \delta b_g\end{array}\right]=\left[\begin{array}{c}{R}_w^{b_k}\left(p_{b_{k+1}}^w-p_{b_k}^w-v_{b_k}^w\Delta t_k+\frac{1}{2}{g}^w\Delta t_k^2\right)-{\alpha }_{b_{k+1}}^{b_k}\\ 2{\left[{\gamma }_{b_{k+1}}^{b_k-1}\otimes q_{b_k}^{w-1}\otimes q_{b_{k+1}}^w\right]}_{xyz}\\ \begin{array}{c}{R}_w^{b_k}\left(v_{b_{k+1}}^w-v_{b_k}^w+g^w\Delta t_k\right)-{\beta }_{b_{k+1}}^{b_k}\\ b_{a_{b_{k+1}}}-b_{a_k}\\ b_{{\omega }_{k+1}}-b_{{\omega }_{b_k}}\end{array}\end{array}\right]\text{\hspace{1em}(13)}$$这里还有一点需要注意的是，公式中的预积分符号用的是${\alpha }_{b_{k+1}}^{b_k}$、${\beta }_{b_{k+1}}^{b_k}$和${\gamma }_{b_{k+1}}^{b_k}$，而不是${\hat{\alpha }}_{b_{k+1}}^{b_k}$、${\hat{\beta }}_{b_{k+1}}^{b_k}$和${\hat{\gamma }}_{b_{k+1}}^{b_k}$，因此应该用公式(6)中的值，对应代码为integration_base.h里的evaluate函数：

//提取雅克比矩阵
Eigen::Matrix3d dp_dba = jacobian.block<3, 3>(O_P, O_BA);
Eigen::Matrix3d dp_dbg = jacobian.block<3, 3>(O_P, O_BG);
Eigen::Matrix3d dq_dbg = jacobian.block<3, 3>(O_R, O_BG);
Eigen::Matrix3d dv_dba = jacobian.block<3, 3>(O_V, O_BA);
Eigen::Matrix3d dv_dbg = jacobian.block<3, 3>(O_V, O_BG);

Eigen::Vector3d dba = Bai - linearized_ba;
Eigen::Vector3d dbg = Bgi - linearized_bg;

//计算修正后的位置、速度和旋转值
Eigen::Quaterniond corrected_delta_q = delta_q * Utility::deltaQ(dq_dbg * dbg);
Eigen::Vector3d corrected_delta_v = delta_v + dv_dba * dba + dv_dbg * dbg;
Eigen::Vector3d corrected_delta_p = delta_p + dp_dba * dba + dp_dbg * dbg;

//计算误差
residuals.block<3, 1>(O_P, 0) = Qi.inverse() * (0.5 * G * sum_dt * sum_dt + Pj - Pi - Vi * sum_dt) - corrected_delta_p;
residuals.block<3, 1>(O_R, 0) = 2 * (corrected_delta_q.inverse() * (Qi.inverse() * Qj)).vec();
residuals.block<3, 1>(O_V, 0) = Qi.inverse() * (G * sum_dt + Vj - Vi) - corrected_delta_v;
residuals.block<3, 1>(O_BA, 0) = Baj - Bai;
residuals.block<3, 1>(O_BG, 0) = Bgj - Bgi;

（2）优化变量

与$b_k$和$b_{k+1}$帧之间残差有关的变量如下：
$$\left[p_{b_k}^w,q_{b_k}^w\right],\left[v_{b_k}^w,b_{a_k},b_{{\omega }_k}\right],\left[p_{b_{k+1}}^w,q_{b_{k+1}}^w\right],\left[v_{b_{k+1}}^w,b_{a_{k+1}},b_{{\omega }_{k+1}}\right]$$

（3）雅克比矩阵

这个雅克比矩阵指的是高斯牛顿法求解时需要用到的残差相对于优化变量的雅克比矩阵，对应的代码在imu_factor.h文件的Evaluate函数中，按照上面优化变量的分类，列出公式和代码如下：$$J[0{]}^{15\times 7}=\left[\frac{\partial r_B}{\partial p_{b_k}^w},\frac{\partial r_B}{\partial q_{b_k}^w}\right]=\left[\begin{array}{cc}-R_w^{b_k}& {\left[R_w^{b_k}\left(p_{b_{k+1}}^w-p_{b_k}^w-v_{b_k}^w\Delta t_k+\frac{1}{2}{g}^w\Delta t_k^2\right)\right]}^{\wedge }\\ 0& -\mathcal{L}-\mathcal{L}\left[q_{b_{k+1}}^{w-1}\otimes q_{b_k}^w\right]\mathcal{R}\left[{\gamma }_{b_{k+1}}^{b_k}\right]\\ 0& {\left[R_w^{b_k}\left(v_{b_{k+1}}^w-v_{b_k}^w+g^w\Delta t_k\right)\right]}^{\wedge }\\ 0& 0\\ 0& 0\end{array}\right]$$对应代码：

Eigen::Matrix3d dq_dbg = pre_integration->jacobian.template block<3, 3>(O_R, O_BG);
if (jacobians[0])
{
    Eigen::Map> jacobian_pose_i(jacobians[0]);
    jacobian_pose_i.setZero();
    jacobian_pose_i.block<3, 3>(O_P, O_P) = -Qi.inverse().toRotationMatrix();
    jacobian_pose_i.block<3, 3>(O_P, O_R) = Utility::skewSymmetric(Qi.inverse() * (0.5 * G * sum_dt * sum_dt + Pj - Pi - Vi * sum_dt));
	Eigen::Quaterniond corrected_delta_q = pre_integration->delta_q * Utility::deltaQ(dq_dbg * (Bgi - pre_integration->linearized_bg));
	jacobian_pose_i.block<3, 3>(O_R, O_R) = -(Utility::Qleft(Qj.inverse() * Qi) * Utility::Qright(corrected_delta_q)).bottomRightCorner<3, 3>();
    jacobian_pose_i.block<3, 3>(O_V, O_R) = Utility::skewSymmetric(Qi.inverse() * (G * sum_dt + Vj - Vi));
    jacobian_pose_i = sqrt_info * jacobian_pose_i;
}

$$J[1{]}^{15\times 9}=\left[\frac{\partial r_B}{\partial v_{b_k}^w},\frac{\partial r_B}{\partial b_{a_k}},\frac{\partial r_B}{\partial b_{w_k}}\right]=\left[\begin{array}{ccc}-R_w^{b_k}\Delta t& -J_{b_a}^{\alpha }& -J_{b_{\omega }}^{\alpha }\\ 0& 0& -\mathcal{L}\left[q_{b_{k+1}}^{w-1}\otimes q_{b_k}^w\otimes {\gamma }_{b_{k+1}}^{b_k}\right]J_{b_{\omega }}^{\gamma }\\ -R_w^{b_k}& -J_{b_a}^{\beta }& -J_{b_{\omega }}^{\beta }\\ 0& -I& 0\\ 0& 0& -I\end{array}\right]$$
对应代码：

Eigen::Matrix3d dp_dba = pre_integration->jacobian.template block<3, 3>(O_P, O_BA);
Eigen::Matrix3d dp_dbg = pre_integration->jacobian.template block<3, 3>(O_P, O_BG);
Eigen::Matrix3d dv_dba = pre_integration->jacobian.template block<3, 3>(O_V, O_BA);
Eigen::Matrix3d dv_dbg = pre_integration->jacobian.template block<3, 3>(O_V, O_BG);
if (jacobians[1])
{
    Eigen::Map> jacobian_speedbias_i(jacobians[1]);
    jacobian_speedbias_i.setZero();
    jacobian_speedbias_i.block<3, 3>(O_P, O_V - O_V) = -Qi.inverse().toRotationMatrix() * sum_dt;
    jacobian_speedbias_i.block<3, 3>(O_P, O_BA - O_V) = -dp_dba;
    jacobian_speedbias_i.block<3, 3>(O_P, O_BG - O_V) = -dp_dbg;
    jacobian_speedbias_i.block<3, 3>(O_V, O_V - O_V) = -Qi.inverse().toRotationMatrix();
    jacobian_speedbias_i.block<3, 3>(O_V, O_BA - O_V) = -dv_dba;
    jacobian_speedbias_i.block<3, 3>(O_V, O_BG - O_V) = -dv_dbg;
    jacobian_speedbias_i.block<3, 3>(O_BA, O_BA - O_V) = -Eigen::Matrix3d::Identity();
    jacobian_speedbias_i.block<3, 3>(O_BG, O_BG - O_V) = -Eigen::Matrix3d::Identity();
    jacobian_speedbias_i = sqrt_info * jacobian_speedbias_i;
}

$$J[2{]}^{15\times 7}=\left[\frac{\partial r_B}{\partial p_{b_{k+1}}^W,}\frac{\partial r_B}{\partial q_{b_{k+1}}^w}\right]=\left[\begin{array}{cc}{R}_w^{b_k}& 0\\ 0& \mathcal{L}\left[{\gamma }_{b_{k+1}}^{b_k-1}\otimes q_{b_k}^{w-1}\otimes q_{b_{k+1}}^w\right]\\ 0& 0\\ 0& 0\\ 0& 0\end{array}\right]$$对应代码：

if (jacobians[2])
{
    Eigen::Map> jacobian_pose_j(jacobians[2]);
    jacobian_pose_j.setZero();
    jacobian_pose_j.block<3, 3>(O_P, O_P) = Qi.inverse().toRotationMatrix();
    jacobian_pose_j = sqrt_info * jacobian_pose_j;
}

$$J[3{]}^{15\times 9}=\left[\frac{\partial r_B}{\partial v_{b_{k+1}}^w},\frac{\partial r_B}{\partial b_{a_{k+1}}},\frac{\partial r_B}{\partial b_{w_{k+1}}}\right]=\left[\begin{array}{ccc}0& 0& 0\\ 0& 0& 0\\ R_w^{b_k}& 0& 0\\ 0& I& 0\\ 0& 0& I\end{array}\right]$$对应代码：

if (jacobians[3])
{
    Eigen::Map> jacobian_speedbias_j(jacobians[3]);
    jacobian_speedbias_j.setZero();
    jacobian_speedbias_j.block<3, 3>(O_V, O_V - O_V) = Qi.inverse().toRotationMatrix();
    jacobian_speedbias_j.block<3, 3>(O_BA, O_BA - O_V) = Eigen::Matrix3d::Identity();
    jacobian_speedbias_j.block<3, 3>(O_BG, O_BG - O_V) = Eigen::Matrix3d::Identity();
    jacobian_speedbias_j = sqrt_info * jacobian_speedbias_j;
}

我这里不厌其烦地把公式对应的代码全部搬过来主要还是想说明这篇博客的主体，预积分的用处，在$J[0]$和$J[1]$中可以看到，我们是利用到了预积分求解的雅克比矩阵里面子矩阵，此外，每个雅克比矩阵最后一步都乘以了sqrt_info这个变量，这个变量怎么来的呢？是通过预积分时获得的误差的协方差获得的，如下：

Eigen::Matrix sqrt_info = Eigen::LLT>(pre_integration->covariance.inverse()).matrixL().transpose();

至于为什么要进行三角分解是因为ceres库使用的原因，到这里应该就能很清楚地看明白预积分的作用了，当然，预积分不仅仅只用在后端优化，在初始化进行视觉IMU标定时也用到了预积分，不过我觉得最核心部分就在这里了吧。

4. 总结

这里最后再总结下，这篇博客主要是从预积分的推导开始，最后在后端优化中说明的了它的用处，这里可以再回到我们的第一个问题，为什么要预积分？还是以这张图为例：

举一个例子，加入现在获得了第k+1帧图像，在程序里面图像的回调函数中会利用k帧到k+1帧的预积分结果以及两帧的位姿进行后端优化，而优化的同时呢，IMU也不断传来数据，假如我们采用的不是预积分的话，当IMU数据已经积分到蓝色箭头处，此时后端优化完成，这个时候k+1帧的位姿和优化前的不一样的，唉呀妈呀，是不是就得重新从k+1帧开始积分，这样当然不行，于是乎我们就采用了预积分的方法，预积分的结果和k+1帧的位姿没关系，所以不需要重新积分，当我们预积分完成之后，直接拿k+1帧和k+2帧的位姿再进行后端优化就可以了，这就是为什么要预积分的原因。

这是我的个人理解，如果有不对的欢迎指正！