记一次看着自己被踢出前100的双周赛——Leetcode第23场双周赛
记一次看着自己被踢出前100的双周赛——Leetcode第23场双周赛
整体来说,这是一个套让我坐下来很顺手的卷子,总共花了45分钟左右排名92,但是由于之前三个错误提交,被踢到了156。(以后提交需谨慎啊!)
5360. 统计最大组的数目
题目描述
题目来源:https://leetcode-cn.com/problems/count-largest-group
给你一个整数 n 。请你先求出从 1 到 n 的每个整数 10 进制表示下的数位和(每一位上的数字相加),然后把数位和相等的数字放到同一个组中。
请你统计每个组中的数字数目,并返回数字数目并列最多的组有多少个。
示例 1:
输入:n = 13
输出:4
解释:总共有 9 个组,将 1 到 13 按数位求和后这些组分别是:
[1,10],[2,11],[3,12],[4,13],[5],[6],[7],[8],[9]。总共有 4 个组拥有的数字并列最多。
示例 2:
输入:n = 2
输出:2
解释:总共有 2 个大小为 1 的组 [1],[2]。
题解
这题贡献了我第一个错误提交:我没看清从0开始还是从1开始。(以后真的要注意)。操作起来很简单,对每个从1到n的数都进行处理(我这里用递归的方式,感觉这样压栈会比较快。)
def Process(n):
if n < 10: return n
return Process(n//10) + n%10
接下来,以返回值作为键,将其放在一个字典下,并利用字典的排序,找出具有最大长度的列表,并计算。(实际上可以优化到只统计出现数字就可以,不用保存每个元素,不过比赛的时候没想这么多)
class Solution(object):
def countLargestGroup(self, n):
def Process(n):
if n < 10: return n
return Process(n//10) + n%10
dic = {}
for i in range(1, n+1):
temp = Process(i)
if temp not in dic:
dic[temp] = [i]
else:
dic[temp].append(i)
lst = sorted(dic.items(), key = lambda x:len(x[1]), reverse = True)
n = len(lst[0][1])
count = 0
for item in lst:
if len(item[1]) != n: break
count += 1
return count
5362. 构造 K 个回文字符串
题目描述
题目来源:https://leetcode-cn.com/problems/construct-k-palindrome-strings
探索题库圈子竞赛面试职位商店下载 App会员中心0题目描述评论 (6)题解(19)提交记录5362. 构造 K 个回文字符串难度中等2给你一个字符串 s 和一个整数 k 。请你用 s 字符串中 所有字符 构造 k 个非空 回文串 。
如果你可以用 s 中所有字符构造 k 个回文字符串,那么请你返回 True ,否则返回 False 。
示例 1:
输入:s = "annabelle", k = 2
输出:true
解释:可以用 s 中所有字符构造 2 个回文字符串。
一些可行的构造方案包括:"anna" + "elble","anbna" + "elle","anellena" + "b"
示例 2:
输入:s = "leetcode", k = 3
输出:false
解释:无法用 s 中所有字符构造 3 个回文串。
题解
首先,考虑到回文串有如下性质:在一个回文串中,一定不会出现多于1个的 出现次数为奇数的字母。那我们只需要考虑原字符串中出现次数为奇数的字符个数。
同时,考虑到边界情况:如果分解数量大于字符数量,那肯定是无法分解的;如果分解数量等于字符数量,那就每个字符为一个回文串即可。
from collections import Counter
class Solution(object):
def canConstruct(self, s, k):
if k > len(s): return False
if k == len(s): return True
dic = Counter(s)
cnt = 0
for i in dic:
if dic[i] % 2: cnt += 1
return cnt <= k
5361. 圆和矩形是否有重叠
题目描述
题目来源:https://leetcode-cn.com/problems/circle-and-rectangle-overlapping
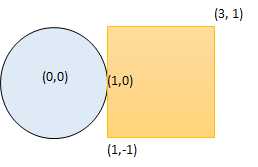
给你一个以 (radius, x_center, y_center) 表示的圆和一个与坐标轴平行的矩形 (x1, y1, x2, y2),其中 (x1, y1) 是矩形左下角的坐标,(x2, y2) 是右上角的坐标。
如果圆和矩形有重叠的部分,请你返回 True ,否则返回 False 。
换句话说,请你检测是否 存在 点 (xi, yi) ,它既在圆上也在矩形上(两者都包括点落在边界上的情况)。
输入:radius = 1, x_center = 0, y_center = 0, x1 = 1, y1 = -1, x2 = 3, y2 = 1
输出:true
解释:圆和矩形有公共点 (1,0)
输入:radius = 1, x_center = 0, y_center = 0, x1 = -1, y1 = 0, x2 = 0, y2 = 1
输出:true
题解
我看到有人直接遍历方块里的点和圆里的点,实际上不用这样。实际上,这是一个与输入数值无关时间复杂度的题目。
我们需要判断两点:
- 是否有嵌套:包含圆套方、方套圆。
- 是否有相交或相切:要考虑正方形四条边是否与圆有交点。
第一个问题就很简单了,分为两种情况:
- 正方形四个顶点都在圆中:到圆心的距离小于半径
- 正方形包含圆:圆到四条边的距离大于半径。
写起来也非常方便:(别看这么多,实际上大部分都是写了第一个,复制黏贴的)
if x0 >= x1 and x0 <= x2 and y0 >= y1 and y0 <= y2: return True
radius2 = pow(r, 2)
if pow(x1 - x0, 2) + pow(y1 - y0, 2) <= radius2 and pow(x2 - x0, 2) + pow(y1 - y0, 2) <= radius2 and pow(x1 - x0, 2) + pow(y2 - y0, 2) <= radius2 and pow(x2 - x0, 2) + pow(y2 - y0, 2) <= radius2:
return True
第二个问题稍稍有点复杂,因为涉及到边际判定的问题。考虑到公式:
( x − x 0 ) 2 + ( y − y 0 ) 2 = r 2 (x-x_0)^2+(y-y_0)^2=r^2 (x−x0)2+(y−y0)2=r2
这是圆周公式,如果我们固定了 x = x 1 , x = x 2 x=x_1,x=x_2 x=x1,x=x2 或是 y = y 1 , y = y 2 y=y_1,y=y_2 y=y1,y=y2 中一个的话,我们就能得到这个圆与矩形四条边的交点,比如这里判定到直线 x = x 1 x=x_1 x=x1 的交点,那:
y = y 0 ± r 2 − ( x − x 0 ) 2 y=y_0\pm \sqrt{r^2-(x-x_0)^2} y=y0±r2−(x−x0)2
当然还是要保证根号下大于0,如果不大于0则肯定说明无交点。(考虑全部四条边就能得到最终结果)一般有两个交点的话,判断交点是否超过两个顶点即可。代码如下
class Solution(object):
def checkOverlap(self, r, x0, y0, x1, y1, x2, y2):
if x0 >= x1 and x0 <= x2 and y0 >= y1 and y0 <= y2: return True
radius2 = pow(r, 2)
if pow(x1 - x0, 2) + pow(y1 - y0, 2) <= radius2 and pow(x2 - x0, 2) + pow(y1 - y0, 2) <= radius2 and pow(x1 - x0, 2) + pow(y2 - y0, 2) <= radius2 and pow(x2 - x0, 2) + pow(y2 - y0, 2) <= radius2:
return True
# line x1
dis = pow(r, 2) - pow(x0 - x1, 2)
if dis >= 0:
sqt = pow(dis, 0.5)
ans1, ans2 = y0 + sqt, y0 - sqt
if ans1 <= y2 and ans1 >= y1: return True
if ans2 <= y2 and ans2 >= y1: return True
# line x2
dis = pow(r, 2) - pow(x0 - x2, 2)
if dis >= 0:
sqt = pow(dis, 0.5)
ans1, ans2 = y0 + sqt, y0 - sqt
if ans1 <= y2 and ans1 >= y1: return True
if ans2 <= y2 and ans2 >= y1: return True
# line y1
dis = pow(r, 2) - pow(y0 - y1, 2)
if dis >= 0:
sqt = pow(dis, 0.5)
ans1, ans2 = x0 + sqt, x0 - sqt
if ans1 <= x2 and ans1 >= x1: return True
if ans2 <= x2 and ans2 >= x1: return True
# line y2
dis = pow(r, 2) - pow(y0 - y2, 2)
if dis >= 0:
sqt = pow(dis, 0.5)
ans1, ans2 = x0 + sqt, x0 - sqt
if ans1 <= x2 and ans1 >= x1: return True
if ans2 <= x2 and ans2 >= x1: return True
return False
5363. 做菜顺序
题目描述
题目来源:https://leetcode-cn.com/problems/reducing-dishes
一个厨师收集了他 n 道菜的满意程度 satisfaction ,这个厨师做出每道菜的时间都是 1 单位时间。
一道菜的 「喜爱时间」系数定义为烹饪这道菜以及之前每道菜所花费的时间乘以这道菜的满意程度,也就是 time[i]*satisfaction[i] 。
请你返回做完所有菜 「喜爱时间」总和的最大值为多少。
你可以按 任意 顺序安排做菜的顺序,你也可以选择放弃做某些菜来获得更大的总和。
示例 1:
输入:satisfaction = [-1,-8,0,5,-9]
输出:14
解释:去掉第二道和最后一道菜,最大的喜爱时间系数和为 (-1*1 + 0*2 + 5*3 = 14) 。每道菜都需要花费 1 单位时间完成。
示例 2:
输入:satisfaction = [4,3,2]
输出:20
解释:按照原来顺序相反的时间做菜 (2*1 + 3*2 + 4*3 = 20)
题解
这是打着困难标签的简单题,为什么这么说呢?其实只需要用贪心+遍历的思路就可以了。这题的意思其实就是:最好吃的菜要放到最后。那我们对评分进行排序,查看从哪道菜开始做,能得到最高的评分就可以。(当然你要注意如果出现负评分,那还不如不做菜)
class Solution(object):
def maxSatisfaction(self, sat):
sat.sort()
n = len(sat)
max_ = -float('inf')
for j in range(n):
count = 0
for i in range(n-j):
count += (i+1) * sat[j + i]
max_ = max(max_, count)
if sat[j] > 0: break # 优化项,读者可以自己考虑为什么,如果有疑问可以评论
return max(0, max_)
赛后总结
提交错误实际上真的挺坑的,所以大家以后一定要读清题,尽量考虑全部边界条件。