Java最短路径:Floyd(弗洛伊德)算法、最短路径问题、思路分析、代码实现
Floyd(弗洛伊德)算法
dijkstra算法与floyd算法的区别:
迪杰斯特拉算法通过选定的被访问顶点,求出从出发访问顶点到其他顶点的最短路径;
弗洛伊德算法中每一个顶点都是出发访问点,所以需要将每一个顶点看做被访问顶点,求出从每一个顶点到其他顶点的最短路径。
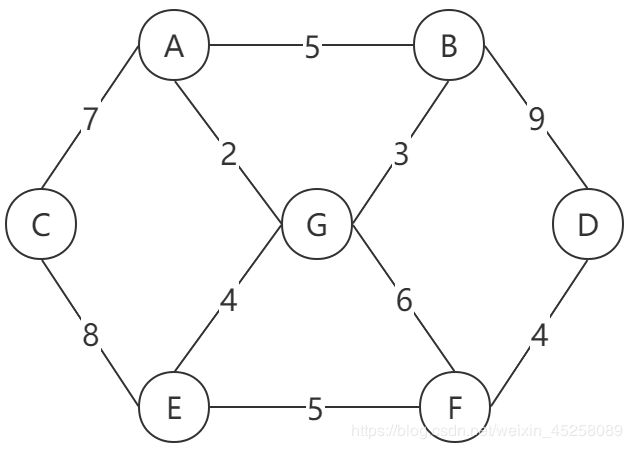
案例:最短路径问题
这里有6个村庄,分别是A、B、C、D、E、F,从G点出发需要将邮件分别送到这6个村庄,各个村庄有不同的路线,路线上都标有公里数,计算各个村庄到各个村庄的最短距离?
. 思路分析
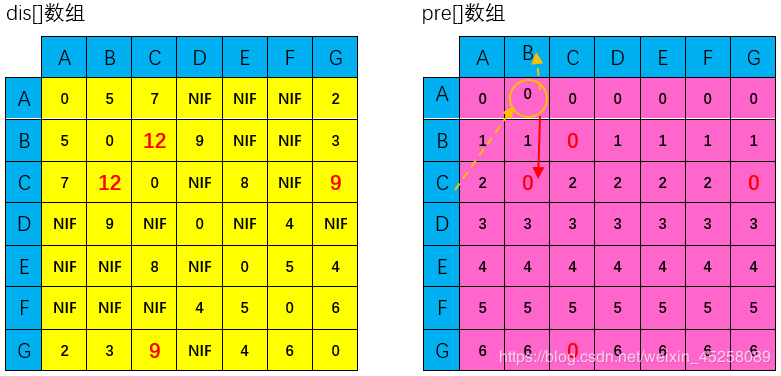
如果已A为中间顶点,即可能的路线为:
如此往复,就会得到每个顶点到达每个顶点的最短距离。
. 代码实现
public class Floyd {
private static final int NIF = 65535;
public static void main(String[] args) {
char vertexData[] = {'A','B','C','D','E','F','G'};
int weight[][] = {
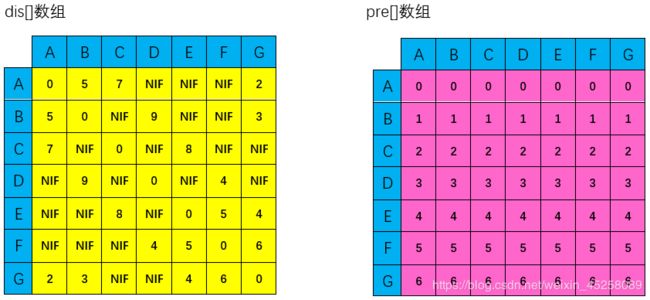
{0, 5, 7, NIF, NIF, NIF, 2},
{5, 0, NIF, 9, NIF, NIF, 3},
{7, NIF, 0, NIF, 8, NIF, NIF},
{NIF, 9, NIF, 0, NIF, 4, NIF},
{NIF, NIF, 8, NIF, 0, 5, 4},
{NIF, NIF, NIF, 4, 5, 0, 6},
{2, 3, NIF, NIF, 4, 6, 0}
};
FloydGraph floydGraph = new FloydGraph(vertexData, weight);
floydGraph.floydAlgorithm();
floydGraph.showRoad();
}
}
class FloydGraph{
private char[] vertexData; // 记录顶点数据
private int[][] dis; // 记录最短路径
private int[][] pre; // 记录前驱顶点
/**
* 构造方法,初始化
* @param vertexData 顶点数据
* @param weight 权值
*/
public FloydGraph(char[] vertexData, int[][] weight) {
this.vertexData = vertexData;
this.dis = weight;
// 初始化前驱顶点,默认初始化前驱顶点为其本身
this.pre = new int[vertexData.length][vertexData.length];
for (int i = 0; i < pre.length; i++) {
Arrays.fill(pre[i],i);
}
}
/**
* 弗洛伊德算法,经过层层遍历,就会得到每个点到达每个点的最短距离
*/
public void floydAlgorithm(){
int len = 0;
// k表示中间顶点
for (int k = 0; k < dis.length; k++) {
// i表示开始顶点
for (int i = 0; i < dis.length; i++) {
// j表示到达顶点
for (int j = 0; j < dis.length; j++) {
// 从i出发,经过k,到达j的距离
len = dis[i][k] + dis[k][j];
// 如果i到j的距离大于i经过k到达j的距离,那么就将i经过k到达j的距离赋值
if (len < dis[i][j]){
dis[i][j] = len;
pre[i][j] = pre[k][j]; // 获得新的前驱节点
}
}
}
}
}
// 展现出最终结果
public void showRoad(){
for (int i = 0; i < dis.length; i++) {
for (int j = 0; j < dis.length; j++) {
System.out.print(vertexData[i]+"->"+vertexData[j]+":"+dis[i][j]+" ");
}
System.out.println();
}
}
}
结果:
A->A:0 A->B:5 A->C:7 A->D:12 A->E:6 A->F:8 A->G:2
B->A:5 B->B:0 B->C:12 B->D:9 B->E:7 B->F:9 B->G:3
C->A:7 C->B:12 C->C:0 C->D:17 C->E:8 C->F:13 C->G:9
D->A:12 D->B:9 D->C:17 D->D:0 D->E:9 D->F:4 D->G:10
E->A:6 E->B:7 E->C:8 E->D:9 E->E:0 E->F:5 E->G:4
F->A:8 F->B:9 F->C:13 F->D:4 F->E:5 F->F:0 F->G:6
G->A:2 G->B:3 G->C:9 G->D:10 G->E:4 G->F:6 G->G:0