神经网络图像输入零均值化的作用
神经网络图像输入零均值化的作用
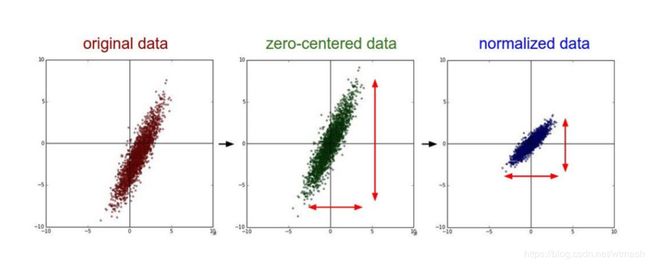
最近有和同学探讨到为什么CNN在做图像识别相关任务时,对图像需要进行零均值化,CS231N里面有进行讲述,但讲得其实不是很清楚,比较难理解,所以在这里做一下较为详细的说明。
1 归一化、标准化和零均值化基本概念
首先介绍一下归一化(Normalization)、标准化(Standardization)以及零均值化(zero-mean)分别的公式和概念。归一化的公式为
x ∗ = x − x m i n x m a x − x m i n x^*=\frac{x-x_{min}}{x_{max}-x_{min}} x∗=xmax−xminx−xmin
其中 x x x为某个特征的原始值, x m i n x_{min} xmin为该特征在所有样本中的最小值, x m a x x_{max} xmax为该特征在所有样本中的最大值, x ∗ x^* x∗为经过归一化处理后的特征值。可以看出,通过该公式,某个特征的值会被映射到[0,1]之间,消除量纲对最终结果的影响,使不同的特征具有可比性。
标准化的公式为
x ∗ = x − μ σ x^* = \frac{x-\mu}{\sigma} x∗=σx−μ
其中 x x x为某个特征的原始值, μ \mu μ为该特征在所有样本中的平均值, σ \sigma σ为该特征在所有样本中的标准差, x ∗ x^* x∗为经过标准化处理后的特征值。即将原值减去均值后除以标准差,使得得到的特征满足均值为0,标准差为1的正态分布。
归一化和标准化都可以消除量纲的影响,使得原本可能分布相差较大的特征对模型有相同权重的影响,在传统机器学习的数据预处理中使用得非常普遍,而具体应该选择归一化还是标准化呢,如果把所有维度的变量一视同仁,在最后计算距离中发挥相同的作用应该选择标准化,如果想保留原始数据中由标准差所反映的潜在权重关系或数据不符合正态分布时应该选择归一化。另外,标准化更适合现代嘈杂大数据场景。
考虑我们对于图像数据做预处理的情况,图像数据的特征实际上是图像上的像素点,比如 224 × 224 × 3 224\times224\times3 224×224×3的图像,一共有150528个像素点,每个像素点也就是一个特征。那么图像的特点就是每个像素点的取值范围都在[0,255]之间,所以不同特征的分布是一样的,不存在量纲的问题,对于模型影响是一样的,所以归一化或标准化是不必要的,而只需要做零均值化。
零均值化在Alexnet论文中是这么说的:“We did not pre-process the images in any other way, except for subtracting the mean activity over the training set from each pixel. ” 即将每个像素的值减去训练集上所有像素值的平均值,比如已计算得所有像素点的平均值为128,所以减去128后,现在的像素值域即为[-128,127],即满足均值为零。而在VGG论文中,关于零均值化是这么说的:"The only preprocessing we do is subtracting the mean RGB value, computed on the training set, from each pixel. ",即对于RGB三通道分开处理,每个通道的像素点减去对应通道所有像素点的平均值。也使得处理后的像素满足均值为零。
我之前预处理的一种做法是对于每个样本的每个通道,取该通道的所有像素的平均值来进行相减,使得每个样本的每个通道满足零均值,但这样会导致一个问题,就是不同样本的像素分布是不一样的,平均值也是不一样的,如果按我那样处理,可能会导致相同的像素值在不同的图像上的处理后的结果是不一样的,那就可能会影响效果了,所以零均值化还是尽量按照之前介绍的两种方法来做。
2 零均值化的作用
那为什么需要做零均值化呢。在CS231N里的说法是零均值化可以避免“Z型更新”的情况,这样可以加快神经网络的收敛速度。下面将分别以Sigmoid、tanh以及ReLu三个最为经典的激活函数来分别说明。
2.1 sigmoid函数
首先以Sigmoid为激活函数来作为例子。如图2为Sigmoid函数的图像,公式如下:
S i g m o i d ( x ) = 1 1 + e − x Sigmoid(x)=\frac{1}{1+e^{-x}} Sigmoid(x)=1+e−x1

可以看出,Sigmoid函数的值域是(0,1)。假设我们对数据不做零均值化,那么对于神经网络第一个隐藏层来讲,输入的数据 X X X就全是正值(因为原始像素数值属于[0,255])。以第一个隐藏层的某一个神经元为例,当进行反向传播算法,梯度从反向到达该神经元时,根据链式法则,对权值w的梯度为全局传过来的梯度乘以激活函数Sigmoid对于w的梯度,即为公式
∂ L ∂ w = ∂ L ∂ f ⋅ ∂ f ∂ w \frac{\partial L}{\partial w}=\frac{\partial L}{\partial f} \cdot \frac{\partial f}{\partial w} ∂w∂L=∂f∂L⋅∂w∂f
其中L为上层传下来的梯度,f为当前的激活函数Sigmoid函数。对于某一个神经元来讲,上层传下来的梯度是一样的,而激活函数也是Sigmoid函数,所以 ∂ L ∂ f \frac{\partial L}{\partial f} ∂f∂L对于所有的w来说都是相同的,而Sigmoid函数的求导公式如下:
s i g m o i d ( x ) ′ = ( 1 1 + e − x ) ′ = 0 ⋅ ( 1 + e − x ) − 1 ⋅ ( − e − x ) ( 1 + e − x ) 2 = e − x ( 1 + e − x ) 2 = 1 + e − x − 1 ( 1 + e − x ) 2 = 1 1 + e − x ⋅ ( 1 − 1 1 + e − x ) = f ( x ) ⋅ ( 1 − f ( x ) ) sigmoid(x)' =(\frac{1}{1+e^{-x}})'\\ =\frac{0\cdot(1+e^{-x})-1\cdot(-e^{-x})}{(1+e^{-x})^{2}}\\ =\frac{e^{-x}}{(1+e^{-x})^{2}}\\ =\frac{1+e^{-x}-1}{(1+e^{-x})^{2}}\\ =\frac{1}{1+e^{-x}}\cdot (1-\frac{1}{1+e^{-x}})\\ =f(x)\cdot(1-f(x))\\ sigmoid(x)′=(1+e−x1)′=(1+e−x)20⋅(1+e−x)−1⋅(−e−x)=(1+e−x)2e−x=(1+e−x)21+e−x−1=1+e−x1⋅(1−1+e−x1)=f(x)⋅(1−f(x))
所以 ∂ f ∂ w \frac{\partial f}{\partial w} ∂w∂f也就是 S i g m o i d ( w x ) Sigmoid(wx) Sigmoid(wx)的对w的求偏导结果为 S i g m o i d ( w x ) ⋅ ( 1 − S i g m o i d ( w x ) ) ⋅ x Sigmoid(wx)\cdot(1-Sigmoid(wx))\cdot x Sigmoid(wx)⋅(1−Sigmoid(wx))⋅x,而已知Sigmoid函数值域为(0,1),所以1-Sigmoid的值域也为(0,1),即结果前两项都为正值,所以 ∂ f ∂ w \frac{\partial f}{\partial w} ∂w∂f的正负只和x的正负有关,此时x全部为正,所以 ∂ f ∂ w \frac{\partial f}{\partial w} ∂w∂f的结果为正,加上 ∂ L ∂ f \frac{\partial L}{\partial f} ∂f∂L对于所有的w来说都是相同的,所以对于第一层的某个神经元的全部w来说,梯度的符号就是 ∂ L ∂ f \frac{\partial L}{\partial f} ∂f∂L的符号,所以这些w的梯度符号全部一致,要么都为正要么都为负,所以该神经元的w都会往同一个方向更新,就会造成"Z型更新"现象,如图3所示。
以只有两维的w1和w2做例子,因为w1和w2的梯度符号一致,要么都为正要么都为负,都为正时则往第一象限变化,都为负时则往第三象限变化,而如果此时最优解在第四象限,则实际训练路径会远远长于最短路径,就会使得网络收敛速度变慢。
所以为了避免Z型更新的情况,将输入进行零均值化,这样某次输入全部为正的可能性就很小,就会是正负掺杂的输入,每个w的梯度符号和输入x相关,也就不会全部都一样,也就不会Z型更新了。
当然这是对于第一层的情况而言的,Sigmoid函数值域是[0,1],有一个特点是非零均值性,也就是输出时非零均值的,经过第一层的激活函数Sigmoid输出后,所有的输出值范围都在[0,1]之间,也就是都大于0,所以后面的第二层、第三层到最后一层,在反向传播时,由于输入的x符号都为正一致,就会出现Z型更新现象,使得网络收敛速度很慢。这就是Sigmoid函数非零均值导致的问题。
所以对于Sigmoid函数来说,第2、3到最后层神经网络,是存在Z型更新问题的,对于输入数据的零均值化,能够避免第一层神经网络的Z型更新问题。
2.2 tanh函数
tanh函数也是经典的激活函数之一,函数图像如图4所示。公式如下:
t a n h ( x ) = s i n h x c o s h x = e x − e − x e x + e − x tanh(x)=\frac{sinhx}{coshx}=\frac{e^{x}-e^{-x}}{e^{x}+e^{-x}} tanh(x)=coshxsinhx=ex+e−xex−e−x
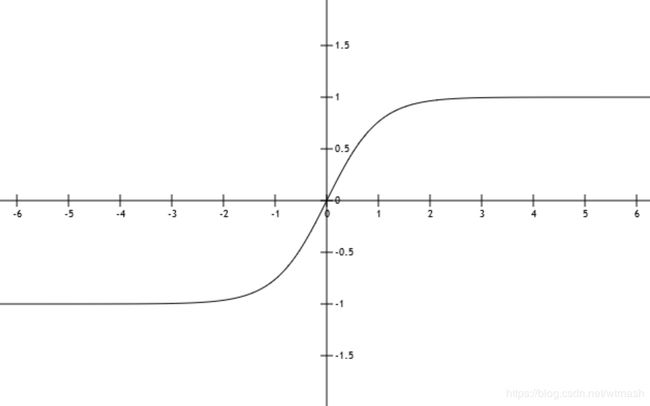
可以看出tanh(x)的值域范围在(-1,1),所以tanh函数是零均值化的。然后tanh(x)的求导公式如下:
t a n h ( x ) ′ = ( e x − e − x e x + e − x ) ′ = ( e x − ( − e − x ) ) ⋅ ( e x + e − x ) − ( e x − e − x ) ⋅ ( e x − e − x ) ( e x + e − x ) 2 = ( e x + e − x ) 2 − ( e x − e − x ) 2 ( e x + e − x ) 2 = 1 − ( e x − e − x e x + e − x ) 2 = 1 − t a n h ( x ) 2 tanh(x)'=(\frac{e^{x}-e^{-x}}{e^{x}+e^{-x}})'\\ =\frac{(e^{x}-(-e^{-x}))\cdot(e^{x}+e^{-x})-(e^{x}-e^{-x})\cdot(e^{x}-e^{-x})}{(e^{x}+e^{-x})^2}\\ =\frac{(e^{x}+e^{-x})^2 - (e^{x}-e^{-x})^2}{(e^{x}+e^{-x})^2}\\ =1-(\frac{e^{x}-e^{-x}}{e^{x}+e^{-x}})^2\\ =1-tanh(x)^2 tanh(x)′=(ex+e−xex−e−x)′=(ex+e−x)2(ex−(−e−x))⋅(ex+e−x)−(ex−e−x)⋅(ex−e−x)=(ex+e−x)2(ex+e−x)2−(ex−e−x)2=1−(ex+e−xex−e−x)2=1−tanh(x)2
还是先以神经网络第一层做例子,如果输入数据不做零均值化,全部为正,此时全局梯度还是和如上文所述,对于某个神经元的所有w来讲是一样的,而本地梯度也就是tanh对w的偏导为
∂ f ∂ w = ( 1 − t a n h ( w x ) 2 ) ⋅ x \frac{\partial f}{\partial w}=(1-tanh(wx)^2)\cdot x ∂w∂f=(1−tanh(wx)2)⋅x
由于tanh(wx)的值域是(-1,1),所以 t a n h ( w x ) 2 tanh(wx)^2 tanh(wx)2的值域为(0,1), 1 − t a n h ( w x ) 2 1-tanh(wx)^2 1−tanh(wx)2的值域也为(0,1),所以该偏导的正负值取决于 x x x的符号,所以当输入全部为正时,对于该神经元的所有w来说梯度的符号也就都一样了,所以更新方向也一致,也就存在Z型更新问题。当将数据进行零均值化后,第一层输入正负掺杂,就能避免Z型更新问题,加快收敛速度。
而由于tanh函数是零均值的,即输出的值范围是在(-1,1),所以对于神经网络的第二、三乃至最后一层,由于输入的值(即上层的输出)都是零均值化的,所以就避免了Z型更新的情况,所以tanh函数的零均值使得其网络收敛速度相较Sigmoid函数更加快。
所以总结一下,tanh函数本身第二、三到最后层的神经网络,在收敛时不存在Z型更新问题,而对于输入数据的零均值化能解决第一层神经网络的Z型更新问题。
2.3 ReLU函数
ReLU是目前最通用的激活函数,函数图像如图5,函数公式为
R e L U = m a x ( 0 , x ) ReLU=max(0,x) ReLU=max(0,x)
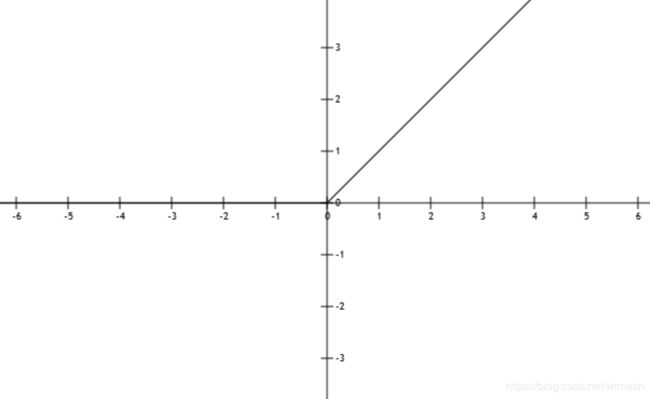
所以ReLU函数明显也是非零均值的。ReLU求导的公式为
f ′ ( x ) = { 1 , x > 0 0 , x ≤ 0 f'(x)=\left\{\begin{array}{cc} 1, & x>0\\ 0, & x\leq0 \end{array}\right. f′(x)={1,0,x>0x≤0
当输入数据不做零均值化时,即输入都大于等于0时,此时和上文一样,第一层接收到的梯度对于该神经元的所有w来说是一样的,而本地梯度为
∂ f ∂ w = { x , w x > 0 0 , w x ≤ 0 \frac{\partial f}{\partial w}=\left\{\begin{array}{cc} x, & wx>0\\ 0, & wx\leq0 \end{array}\right. ∂w∂f={x,0,wx>0wx≤0
由于此时输入x都大于等于0,所以当 w x > 0 wx>0 wx>0时梯度方向仍然只和x符号有关,都为正时该神经元的所有w更新方向仍然一致,也会有Z型更新现象。
而对输入零均值化后,输入正负掺杂,满足 w x > 0 wx>0 wx>0的输入里,x的符号就是正负掺杂的,所以w的更新方向就会不是一致的了,就没有Z型更新现象了。
当然这也只是对于第一层神经元,由于ReLU的输出都是大于等于0的,即它是非零均值的,所以对于第2、3一直到最后层的神经元,在收敛时会有Z型更新问题。