Matryoshka: Fuzzing Deeply Nested Branches
Abstract
灰盒fuzz近年来取得了令人瞩目的进展，从基于启发式的随机变异进化到求解单个分支约束。但是，它们很难解决包含深度嵌套条件语句的路径约束，这些条件语句在图像和视频解码器、网络包分析器和校验和工具中很常见。我们提出了解决这个问题的方法。首先，我们识别目标条件语句的所有控制流相关条件语句。接下来，我们选择污染流相关的条件语句。最后，我们使用三种策略来寻找同时满足所有条件语句的输入。我们在一个叫做Matryoshka1的工具中实现了这种方法，并将其在13个开源程序上的有效性与其他最先进的fuzzer进行了比较。Matryoshka的累积测线和分支覆盖率显著高于AFL、QSYM和Angora。我们手动将Matryoshka发现的碰撞分类为41个独特的新漏洞，并获得12个CVE。我们的评估展示了Matryoshka令人印象深刻的性能的关键技术：在目标条件语句的嵌套约束中，Matryoshka只收集那些可能导致目标无法到达的约束，这大大简化了它必须解决的路径约束。
introduction
Fuzzing是一种自动化的软件测试技术，它成功地发现了现实软件中的许多缺陷。在各种类型的模糊技术中，基于覆盖的greybox模糊技术尤其流行，它优先于分支探索，以便在难以到达的分支中高效地触发bug。与符号执行相比，灰盒模糊避免了昂贵的符号约束求解，因此可以处理大型、复杂的程序。
AFL[2]是一种基本的灰盒fuzz。它让程序报告当前输入是否在运行时探索了新的状态。如果当前输入触发了一个新的程序状态，那么fuzzer将当前输入作为种子保存，以便进一步变异[35]。然而，由于AFL只使用粗糙的试探法对输入进行随机变异，因此很难实现高代码覆盖率。较新的fuzzer使用程序状态来指导输入变异，并显示出比AFL显著的性能改进，例如Vuzzer[30]、Steelix[26]、QSYM[41]和Angora[13]。以Angora为例。它使用动态污点跟踪来确定哪些输入字节流到保护目标分支的条件语句中，然后只对这些相关字节进行变异，而不是对整个输入进行变异，以大幅度减少搜索空间。最后，利用梯度下降法寻找分支约束的解。
然而，这些模糊器在解决包含嵌套条件语句的路径约束时面临困难。分支约束是保护分支的条件语句中的谓词。只有当（1）条件语句是可到达的，并且（2）满足分支约束时，分支才是可到达的。路径约束满足这两个条件。当一个条件语句s被嵌套时，只有当执行路径上的一些先前的条件语句P是可到达的时，s才是可到达的。如果
中的分支约束共享公共输入字节，那么当fuzzer对输入进行变异以满足s中的约束时，它可能会使P中的约束失效，从而使s无法访问。这个问题困扰着前面提到的fuzzer，因为它们无法跟踪控制流，并且污染了条件语句之间的流依赖关系。嵌套条件语句在图像和视频的编码器和解码器、网络包分析器和校验和验证程序中都很常见，它们具有丰富的漏洞历史。尽管混合执行可以解决一些嵌套的约束。结果表明，混合执行引擎会出现过度约束问题，这使得解决约束的代价太高[41]，特别是在实际程序中。
图1在程序readpng中显示了这样一个例子。第6行的谓词嵌套在第4行的谓词中。模糊器很难找到到达第6行假分支的输入，因为输入也必须满足第4行的假分支。当fuzzer试图改变第6行的谓词时，它只改变流入缓冲区[0]的输入字节，但这几乎肯定会导致png_CRC_finish()中的CRC检查失败，这将导致第4行接受真正的分支并返回。
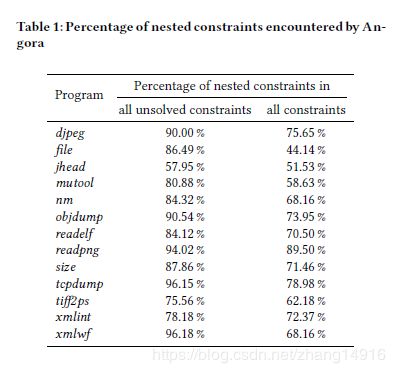
为了评估当前的fuzzer是否难以解决包含嵌套条件语句的路径约束，我们使用Angora作为案例研究。我们在13个开源程序上运行它，这些程序读取结构化输入，因此可能有许多嵌套的条件语句。表1显示，在所有程序中，大多数未解决的路径约束都涉及嵌套的条件语句。在5个程序中，90%以上的未解决约束涉及嵌套条件语句。这表明解决这些约束将显著提高模糊器的覆盖率。
我们设计并实现了一种允许fuzzer探索深度嵌套条件语句的方法。下面以图2中的程序为例。假设当前输入运行第6行的假分支，而fuzzer希望探索第6行的真分支。
- 确定条件语句之间的控制流依赖关系。第一个任务是标识跟踪上第6行之前的所有条件语句，这些语句可能使第6行无法访问。它们包括第2、3和4行，因为如果其中任何一行使用不同的分支，那么第6行将无法访问。第3.3节将描述我们如何使用过程内和过程间的后支配树来查找这些条件语句。
- 确定条件语句之间的污染流依赖关系。在前一步确定的条件语句中，只有第2行和第3行的语句与第6行有污染流依赖关系。这是因为当我们在第6行上进行变异时，这可能会改变第3行的分支选择，从而使第6行无法访问。为了避免这个问题，我们必须保留3号线的分支选择，这可能需要我们同时改变x和y，但这可能会改变2号线的分支选择。因此，2号线和3号线与6号线有污染流依赖关系。相比之下，当我们为了探索6号线的真正分支而进行变异时，4号线的分支选择从未改变，因此它与6号线没有污染流依赖关系。第3.4节将描述我们如何找到这些依赖污染流的条件语句。
- 解决约束。最后，我们需要对输入进行变异以同时满足多个依赖条件语句。换言之，我们需要找到一个既到达第6行又满足其真正分支的新输入。我们提出三个策略。
- 第一种策略保守地假设，如果我们对第6行所依赖的任何条件语句中的任何字节进行变异，那么第6行将变得不可访问。因此，在模糊第6.4行（第3.5.1节）时，此策略避免了这些字节的变异
- 第二种策略人为地保留了第6行在对流入第6行的输入字节进行变异时所依赖的所有条件语句的分支选择。当它找到一个满意的输入时，它验证程序是否可以在不改变分支选择的情况下到达第6行。如果是这样，那么fuzzer成功地解决了这个问题。否则，模糊器将在跟踪上回溯，以在3号线和2号线上尝试此策略。（第3.5.2节）
- 最后一种策略试图找到满足所有依赖条件语句的解决方案。它定义了一个联合约束，其中包括每个依赖条件语句的约束。当fuzzer找到一个满足联合约束的输入时，则保证该输入满足所有相关条件语句中的约束。（第3.5.3节）
我们的方法假设没有特殊结构或属性在被fuzz的程序，比如魔法字节或校验和函数。相反，我们解决嵌套条件语句的一般方法可以自然地处理这些特殊结构。
我们在一个名为Matryoshka的工具中实现了我们的方法，并将其在13个开源程序上的有效性与其他最先进的fuzzer进行了比较。Matryoshka共发现41个独特的新漏洞，并在其中7个程序中获得了12个CVE。Matryoshka令人印象深刻的性能不仅在于它解决嵌套约束的能力，还在于它如何构造这些约束。传统的符号执行收集路径上所有条件语句中的谓词。相比之下，Matryoshka只在目标分支同时依赖于控制流和污染流的条件语句中收集谓词。我们的评估表明，后者只占路径上所有条件语句的一小部分，这大大简化了Matryoshka必须解决的约束。
Background
Greybox fuzzing是一种流行的程序测试方法，它将程序状态监测与随机输入变异结合起来，效果显著。然而，目前最先进的greybox fuzzers无法可靠有效地解决嵌套条件语句。使用启发式（例如，AFL）或原则性变异方法（例如，Angora）的模糊器没有足够的关于条件语句之间的控制流和污染流依赖性的信息来设计能够满足所有相关分支约束的输入。其他使用混合混合混合执行的模糊器，如司钻，由于将路径的整个符号约束具体化，会遇到性能问题[41，42]。QSYM是一个实用的混合执行fuzzer，但它是专门为解决路径上的最后一个约束而定制的，因此面临着与Angora相同的解决嵌套条件语句的挑战。
以Angora为例，我们评估了嵌套条件语句对Angora性能的影响，并在表1中分析了Angora未能解决的8个程序中的约束，其中每个约束对应于程序中的唯一分支。第二列显示嵌套未解决约束的百分比，这取决于控制流和污染流的其他条件语句（第3.4节）。第三列显示所有约束（已解决和未解决）中嵌套的百分比。表1显示，大多数未解决的约束是嵌套的，范围从57.95%到接近100%。研究还表明，嵌套约束占所有约束的很大一部分，从44.14%到89.50%。这些结果表明，解决嵌套约束可以大大提高greybox fuzzers的覆盖率
Design
3.1.problem
最新的覆盖率引导模糊器，例如Angora[13]、QSYM[41]、VUzzer[30]和REDQUEEN[4]，通过解决分支约束来探索新的分支，其中分支约束是保护分支的条件语句中的谓词。这通常包括以下步骤。首先，使用动态污染分析或类似技术确定影响每个条件语句的输入字节。然后，确定输入字节应如何变异，例如计算谓词的梯度并使用梯度下降、匹配幻数字节或使用符号执行解算器。最后，使用变异的输入执行程序，并验证这是否触发条件语句中的另一个分支。
尽管这种方法在解决许多分支约束方面是有效的，但是当目标条件语句在输入变异过程中变得不可访问时，它会失败。
图2显示了一个示例。让变量x、y和z包含不同的输入字节。假设当前输入执行第6行的假分支，目标是探索第6行的真分支。然后，模糊器通过动态字节级污染分析确定它需要更改y中的字节。考虑x和y两个不同的初始值。
- x=0，y=1。如果fuzzer将y变异为3，那么程序将不再到达第6行，因为第3行将采用不同的（false）分支。这使得模糊者在解决分支谓词时无能为力，即使存在满意的赋值y＝2。
- x=1和y=1。在这种情况下，没有一个y值可以同时满足第2行、第3行和第6行的真正分支，除非我们也对x进行了变异。但是，由于x没有流入第6行的条件语句中，fuzzer不知道它应该对x进行变异，因此无论怎样，它都无法找到一个满意的赋值来探索第6行的真正分支用于求解约束的算法。
此示例表明，要执行未探索的分支，有时仅对流入条件语句的输入字节进行变异是不够的，因为这样做可能会使此语句无法访问。人们可以天真地对所有输入字节进行变异，但这会增加许多数量级的搜索空间，使这种方法过于昂贵而不实用
3.2.solution overview
为了克服第3.1节中的问题，我们的关键见解是，当我们模糊条件语句时，必须找到既满足分支约束又保持语句可访问的输入。大多数通过求解分支约束来探索分支的模糊算子只考虑满足性准则，而没有考虑可达性准则。我们提出以下步骤来满足这两个标准，同时改变输入。让我们作为一个条件语句来跟踪这个输入上的程序。我们的目标是改变输入，让我们采取不同的分支。我们调用目标条件语句，并说新输入满足s。
- 确定条件语句之间的控制流依赖关系。标识跟踪上s之前可能使s无法访问的所有条件语句。例如，如果s在图2中的第6行，那么如果第2、3和4行上的任何条件语句采用不同的分支，那么第6行将无法访问。我们称之为s的先验条件语句，这取决于控制流。相比之下，不管5号支线走哪条，6号线总是可以到达的。第3.3节将详细描述此步骤。
- 确定条件语句之间的污染流依赖关系。在s的先前条件语句中，标识那些其相应的输入字节可能必须进行变异以满足s的条件语句。例如，让s成为图2中的第6行。在它的三个先验条件语句中，只有第2行和第3行的那些语句包含可能必须进行变异以满足s的字节（x和y）。我们称这些有效的先验条件语句，这取决于污染流。相比之下，第4行不包含为满足s而必须进行变异的输入字节。第3.4节将详细描述此步骤。
- 解决约束。对有效的先验条件语句中的字节进行变异以满足s.第3.5节将详细描述此步骤。
图3显示了Matryoshka的总体设计，说明了在模糊化过程中如何使用这些策略。
3.3. Determine control flow dependency among conditional statements
对于每个条件语句s，我们希望标识它之前的所有条件语句，这些条件语句如果采用不同的分支，可能会导致s无法访问。路径上的s的紧接的前置条件语句是s的最后一个前置条件语句，即r和s之间没有s的前置条件语句。注意，如果s是t的前置条件语句，而t在u中，那么s是u的一个前置条件语句，这使得我们可以通过传递找到s的所有前置条件语句：从s开始，我们反复找到直接前置条件语句，然后取所有这些语句的并集。
我们提出了两种不同的方法来分别寻找同一函数和不同函数中的立即前置语句。在我们的优化实现中，我们缓存了所有找到的依赖项，以避免重复计算。
3.3.1 程序内紧接前置条件语句
从条件语句s开始，我们返回跟踪。当我们找到第一个条件语句r时，1.在同一个函数中，并且2.那不是后支配。那么r是s的立即前置语句，我们的实现使用了LLVM生成的后支配树
如果我们找不到这样的r，那么s没有过程内的直接先验条件语句，我们将搜索它的程序间直接先验条件语句，如第3.3.2节所述。
3.3.2. 程序间紧接前置条件语句
使用过程间后支配树进行有效的处理是很简单的，但是不幸的是，LLVM并没有提供这样的信息，所以我们设计了以下方法来查找s的过程间前立即条件语句r满足以下所有条件：1.r与s在不同的函数中（我们称之为fr），并且执行s时，fr仍在堆栈上（即，它没有返回），并且让rc是fr执行的最后一个调用指令。rc必须存在，因为r在比s更深的堆栈帧中，如果rc没有后支配r（注意r和rc在相同的函数中），那么r是s的过程间的立即优先语句。
3.3.3不规则的程序间控制流程
除了函数调用之外，程序还可以表现出不规则的过程间控制流，例如涉及exit和longjmp指令的那些流程。如果一个条件语句r至少有一个分支指向一个包含不规则流的基本块，那么即使它的帧不在堆栈上，我们也认为它是它之后所有语句的优先条件语句。如果s是r之后的条件语句，我们将r和r的先验条件语句添加到s的先验条件语句集中。在LLVM中，包含不规则过程间控制流的基本块用不可到达的指令终止。
3.4确定条件语句之间的污染流依赖关系
对于每个条件语句，第3.3节查找其所有先前的条件语句p(s)。设b(s)为流入s的输入字节集，其中s是一个或多个条件语句。当我们对输入进行变异时，只要p(s)中没有条件语句接受不同的分支，就保证s是可到达的。这似乎表明我们应该避免改变b(p(s))中的任何字节。
另一方面，避免改变b(p(s))中的每个字节可能会阻止fuzzer为s找到满意的赋值，如第3.1节所述。以图2为例。让我们模拟程序执行到第6行。根据第3.3.1节，我们确定p(s)由第2、3和4行组成。因此，b(p(s))={x,y,z}；。如果我们保持b(p(s))中的所有字节都是不可变的，那么在试图找到满足s的输入时，就没有输入字节可以变异。
出现问题是因为第3.3节只考虑条件语句之间的控制流依赖性，但是它没有考虑条件语句之间是否存在污染流依赖关系。我们将s,e(s)的有效先验条件语句定义为s的先验条件语句的子集，如果要找到满足s的输入，我们可能需要对在e(s)中流入语句的一些字节进行变异。换言之，如果s的先验条件语句r不是s的有效先验条件语句，则流入r的字节无需进行变异以满足s，这意味着我们可以只考虑有效的先验条件语句而忽略无效的先验条件语句。
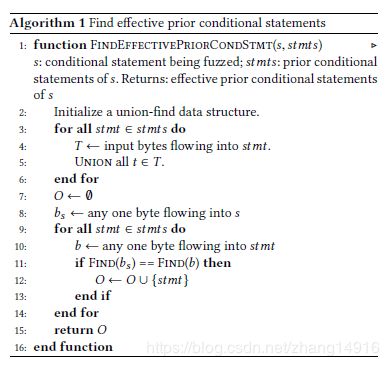
算法1给出了计算有效先验条件语句的算法，该算法依赖于以下性质：如果r是s的有效先验条件语句，q是s的先验条件语句，q和r共享公共输入字节，那么q也是s的有效先验条件语句。
3.5解决约束
第3.4节确定每个条件语句s的有效优先条件语句。一方面，如果我们自由地改变流入其中任何一个的字节，s可能变得不可访问。但另一方面，我们可能需要对其中的一些字节进行变异，以满足s的未探索分支。因此，我们需要确定哪些语句的相关输入字节可能发生变异。我们提出以下三种替代策略。Matryoshka按照这个顺序进行尝试，并为每个策略设定时间预算，以确保整体效率。(1)优先考虑可达性(2)优先满足(3)可达性和可满足性联合优化
每个策略标识一组输入字节上的约束。然后，采用基于梯度的优化方法求解约束条件。这些策略只有当s是嵌套的，即s具有有效的先验条件语句时才提供好处。如果S不是嵌套的，Matryoshka仅仅使用来自Angora或其他模糊体的现有策略来解决分支约束。因此，Matryoshka在解决嵌套条件语句时表现出更好的性能，同时具有与其他fuzzer相同的能力来解决非嵌套条件语句。
3.5.1优先考虑可达性
这种策略悲观地假设，如果我们对任何流入条件语句s的任何有效先验条件语句的字节进行变异，则s可能变得不可访问。因此，该策略通过避免对流入s的任何有效先验条件语句的任何字节进行变异来确保s始终是可到达的。形式上，设b(s)为流入s的字节，b(e(s))为流入s的有效先验条件语句的字节。安哥拉变异了b(s)中的所有字节，这可能导致s变得不可访问。相比之下，Matryoshka的这种策略只对b(s)\b(e(s))中的字节进行变异，即所有流入s但未流入s的有效先验语句的字节。
以图2中的程序为例。当我们模糊s到第3行时，它唯一有效的条件语句是第2行的t。b(s)={x,y}。b(e(s))={x}。使用这种策略，fuzzer只对b(s)\b(e(s))={y}中的字节进行变异。
然而，当我们模糊s到6行时，这个策略失败了。在这种情况下，其有效的先前声明由第2行和第3行的声明组成，因此b(s)={y}，b(e(s))={x,y}。但是b(s)\b(dp(s))= 
。使用这种策略，Matryoshka将无法模糊s，因为它找不到要变异的字节。
3.5.2优先满足
该策略乐观地希望满足条件语句s的变异输入也能到达s，它有一个前向阶段和一个后向阶段。在前向阶段，它对流入s的字节进行变异，同时人为地保留s的所有有效先验条件语句的分支选择，从而保证s始终是可到达的。如果它找到满足S的目标分支的输入，则它正常运行该输入程序（不人为地修复分支选择）。如果此跟踪仍然到达并选择目标分支，则它将成功。否则，它将进入回溯阶段。在这个阶段中，它从s开始，然后按照这个顺序向后模糊s的每个有效先验语句。当它模糊一个这样的语句r时，它避免了对可能流入s的任何字节或r之后的s的任何有效的先验条件语句进行变异。当fuzzer成功地模糊了所有这些有效的先验条件语句时，这个过程就成功了。算法2显示了该算法。
以图2中的程序为例。当我们模糊s到第6行时，它的有效先验条件语句在第3行和第2行。设正确输入为x=1；y=1。在这个输入下，第2行和第3行都取真分支，第6行取假分支。我们的目标是在6号线找到真正的分支。使用这种策略，在前向阶段，模糊器会变异y，同时人为地强制程序在2号线和3号线上采用真正的分支。如果fuzzer发现赋值y=2满足第6行的真正分支，但由于x=1；y=2不满足第3行，它将进入回溯阶段。在此阶段，它将首先模糊3号线。尽管这条线受到两个值fx；yg的影响，因为y流入第6行，fuzzer只会改变x。如果找到一个满意的赋值x=0，它将尝试在x=0；y=2的情况下运行程序，而不会人为地强制执行分支选择。由于此输入到达第3行并满足目标（true）分支，因此模糊化成功。
相比之下，假设fuzzer在模糊第6行时找到了一个满意的赋值y=3。在回溯阶段，当模糊3号线时，由于它只能变异x，因此无法找到满意的赋值。因此，s的模糊化失败了。
3.5.3可达性和可满足性的联合优化
第3.5.1节和第3.5.2节中的两种策略每次搜索一个约束的解决方案。第3.5.1节仅对不会使目标条件语句不可访问的输入字节进行变异，而第3.5.2节则尝试一次满足目标条件语句及其有效的先前条件语句。然而，他们没有找到一个解决方案，我们必须共同优化多个约束。
让s成为目标条件语句。设![f_{i}(x)\leq 0,\forall i\in [1,n]](http://img.e-com-net.com/image/info8/1d00fef86f304cb6b8851a19b705ddb8.gif){kind=small}
表示s的有效先验条件语句的约束，并且
表示s的约束。x是表示输入字节的向量。表2显示了如何将每种类型的比较转换为
。我们的目标是找到一个满足所有![f_{i}(x)\leq 0,i\in [0,n]](http://img.e-com-net.com/image/info8/1d7ba7f804ab4b0fbf548b30a6270f53.gif){kind=small}
。注意，每个
是一个黑箱函数，用条件语句i中的表达式表示输入x的计算。由于的解析形式不可用，许多常用的优化技术，如Lagrange乘子，不适用。
我们提出了一个优化问题的解。定义
。其中纠正
(二进制
运算符输出其操作数的较大值)。因此，
仅当。换句话说，我们将n个优化组合成一个优化。现在我们可以使用梯度下降算法，类似于安哥拉使用的梯度下降算法，来找到一个解。注意到当我们用分化计算g(x)的梯度时，我们需要人工地维持分支选择有效的先决条件声明，以确保这是可以实现的。
让我们重新查看图2中的程序。设[x,y]=[1,3]为初始输入。当我们模糊第6行的目标条件语句s以探索真正的分支时，我们不能仅通过变异y来求解分支约束。使用联合优化，我们将第3行和第2行的s的分支约束及其有效的先验条件语句结合起来构造（通过式1和表2）：
![g([x,y])=R(x-2+\varepsilon )+R(x+y-3+\varepsilon )+R(1-y+\varepsilon ) (\varepsilon=1)](http://img.e-com-net.com/image/info8/70e70e7dacae45238f69b43024d06625.gif){kind=small}
在初始输入[x,y]=[1,3]，g([x,y])=2.使用梯度下降，我们将找到g([x,y])=0的解，其中[x,y]=[0,2]。
3.6检测隐含有效先验条件语句
如果我们不能找到条件语句之间的所有控制流和污染流依赖关系，那么第3.5节中的变异策略可能会失败。第3.3节和第3.4节分别描述了查找所有显式控制流和污染流依赖项的算法。但是，它们无法找到隐式流。图4显示了这样一个例子。第13行的条件语句在函数foo中导致隐式污染流进入fun-ptr，然后隐式确定控制流是程序调用函数条还是其他函数。另外，第3行导致隐式污染流进入变量k，其值将决定第6行谓词的值。因此，第13行和第3行的条件语句都应该是第7行目标语句的有效前置条件语句。但是，由于污染流是隐式的，因此第3.4节中的算法找不到它们。
隐式污染流可以用控制流图来识别[23]。如果谓词被污染，那么该方法污染在条件语句的任一分支中获取新值的所有变量。对于字节级污点跟踪，此方法将谓词的污点标签添加到上述每个变量中。例如，考虑图4中第3行的谓词。由于变量k和n在这个条件语句的一个分支中被赋予了新的值，这个方法将谓词的污点标签（即变量y的污点标签）添加到变量k和n中。但是，这个方法经常导致过度污点或污点爆炸，因为它可能会添加对分析毫无用处的污染标签。例如，在上面的例子中，虽然添加到变量k的污染标签捕获了从第3行到第6行的隐式污染流依赖关系，但是添加到变量n的污染标签是无用的，因为它无助于识别条件语句之间的新污染流依赖关系。更糟糕的是，这些无用的污染标签将进一步传播到程序的其他部分，导致污染爆炸。
我们提出了一种新的方法来识别条件语句之间的隐式控制流和污染流依赖关系，而不会产生巨大的分析开销或污染爆炸。洞察是，我们不需要识别所有的隐式流，而只需要识别那些导致目标条件语句在输入变异期间变得不可访问的流。让我们成为目标条件语句，它在原始输入上是可到达的，但在变异输入上是不可到达的。我们运行程序两次。首先，我们在原始输入上运行程序，并在s之前的路径上记录所有条件语句的分支选择。然后，我们使用一种特殊的处理方法在变异输入上运行程序：当我们遇到条件语句时，我们记录它的分支选择，但强制它接受上次运行时的分支选择（在原始输入上）。因此，两次运行的路径具有相同的条件语句序列。我们按照相反的时间顺序检查从程序开始到s的路径上的所有条件语句。对于每个这样的语句t，如果它还不是由第3.4节中的算法识别的显式有效优先语句，并且如果它在第一次运行（在原始输入上）和第二次运行（在变异输入上）中的分支选择不同，它有一个潜在的控制流或与S的污点流依赖关系，以测试这种依赖性是否真的存在，我们用一个特殊的处理在突变输入上运行程序：我们强制所有以下条件语句像第一次运行一样进行分支选择：(1)路径上t之前的所有条件语句 (2)所有显式有效先验条件语句 (3)所有隐式有效先验条件语句
如果程序不再到达s，那么t确实与s有隐式控制流或污染流依赖关系，我们将它标记为S的隐式有效的先验条件语句。
该算法的复杂性在S之前的条件语句的数目是线性的，它受突变字节的影响，但不是依赖于S的控制流。然而，由于MatRysHKA在输入的一小部分上通过梯度下降来改变输入；我们应该测试的语句数量可能很少