时间序列模型简介

平稳序列
判断样本的平稳性
时间序列模型
参数选择
实验代码

1. 平稳序列

时间序列是一列观测值的集合, 其中每个观测值是在时段观测所得(是自然数 ). 给定时间序列, 如果对任意的, 它满足下列条件:
i.
ii.
iii.
我们把它叫做(弱)平稳(weakly stationary)序列.(下文我们简称平稳序列.)

通俗地讲, 平稳序列的期望, 方差, 协方差不随时间变化. 例如, 服从同一个分布时, 它是平稳的.

例1 下图中的时间序列由生成. 从直观上看, 这个序列是"平稳的".

Fig1. 平稳的时间序列

例2 下图的中的时间序列由生成, 其中, . 它起初有明显地增长, 然后趋于平稳. 利用ADF检验(详情见下文), 我们发现该序列是平稳的(p-value < 0.01).

Fig2. 平稳的时间序列

Remark 弱平稳性的"弱"主要体现在时间序列在全局上是平稳的, 即，时间序列局部是波动的，但整体上看是平稳的, 或者随着时间的变化其样本的均值收敛.

2. 判断样本的平稳性

我们用统计学中假设检验的方法来判断样本的平稳性. 常用的是Augmented Dickey-Fuller(ADF)检验^[1].

Null Hypothesis: 样本中存在unit root^[2]. 如果接受, 则意味着样本是非平稳的.
Alternate Hypothesis: 样本中不存在unit root. 如果拒绝, 则意味着样本是平稳的.

在显著水平的条件下, 我们可以通过计算p-value来接受或者拒绝:

: 接受.
: 拒绝.

Python3中statsmodels.tas.stattools中的adfuller函数^[3]实现了ADF检验. 使用方法如下所示.

from statsmodels.tsa.stattools import adfuller


def test_stationarity(data, alpha=0.05, print_detail=True):
    """ Test stationarity of time series data.
    :param data: time series data, formatted as list
    :param alpha: significance level.
    :param print_detail: if True print additional information. 
    """
    result = adfuller(data)
    is_stationary = True if result[1] <= alpha else False
    if print_detail:
        print('ADF statistic: %f' % result[0])
        print('p-value: %f' % result[1])
        print('critical values:')
        for key, value in result[4].items():
            print('\t%s: %.3f' % (key, value))
    return is_stationary

3. 时间序列模型

前面之所以介绍平稳序列的概念及检验方法, 是因为它是很多基础的时间序列模型的前提假设. 在本节我们介绍一些常见的时间序列模型(更多内容可以参考^[4], ^[5]).

AR(p)

AR代表自回归(Autoregression). 假设时间序列是平稳的, 它可以被表示成如下形式:

是常数.
, 它表示时段的误差(随机变量).
代表自回归阶数.

MA(q)

MA代表移动平均(Moving Average). 假设时间序列是平稳的, 它可以被表示成如下形式:

是常数.
, 它表示时段的误差(随机变量).
代表移动平均阶数.

ARMA(p,q)

ARMA模型是AR和MA的组合. 假设同上. 它可以被表示为如下形式:

是自回归阶数
是移动平均阶数

ARIMA(p,d,q)

ARIMA模型是ARMA模型的推广, 全称是Autoregressive Integrated Moving Average. 当时间序列不满足平稳性时, 我们通常使用差分的技巧把序列变得平稳, 然后再应用ARMA模型.

参数代表差分的阶数. 下面是差分的计算公式(为差分算子):

一阶差分
二阶差分
阶差分

例3 下图是原始的时间序列. 通过观察, 它的均值有明显的上升趋势且不收敛, 因此不是平稳序列(ADF检验的p-value为0.94).

对该序列进行一阶差分后, 我们得到如下平稳的时间序列(p-value为0.00).

ARIMA(p,d,q)(P,D,Q,s)

该记号代表季节性(或周期性)ARIMA模型, 详细的表达式可以参考^[4](4.1 Seasonal ARIMA models), 其中

的意义同上.
代表周期性自回归阶数(前个周期对应观测值的自回归).
代表周期性差分阶数.
代表周期性移动平均阶数(前个周期对应的移动平均).
代表一个周期的长度.

我们可以把它看成两阶段模型: 第一阶段在全局使用ARIMA(p,d,q); 第二阶段通过指定周期长度, 再利用ARIMA(P,Q,D)模型考虑周期之间的关系.

例4 考虑如下周期性的平稳时间序列().

season.png

对序列进行周期性差分: 得到新的时间序列如下图所示(红色部分)

deseason.png

通过使用周期性差分, 我们可以把原有时间序列的周期性移除. 同理, 通过采用周期性的自回归和移动平均系数, 我们可以把周期之间的依赖关系考虑进模型.

例5 考虑周期s=18的数据(蓝色曲线). 用和分别进行预测的结果如下.

不考虑周期性的ARIMA模型的预测结果(灰色曲线)逐渐收敛到时间序列的均值. 由于序列是平稳的, 这样的预测结果符合我们的期望. 考虑到该时间序列有比较强的周期性, 且通过观察发现周期. 在本例中, 我们仅使用周期差分, 最终得到了如图所示(红色曲线)的周期性预测结果.

ARCH(p)

ARCH的全称是Autoregressive Conditionally Heteroscedasticity, 它可以用来考虑样本的方差随着时间变化(或震荡)的时间序列. 设时间序列是平稳的, 模型可以被表示成如下形式:

其中

代表的自回归阶数.

GARCH(p,q)

GARCH即Generalized ARCH, 是ARCH模型的推广^[6]. 设时间序列是平稳的, 模型可以被表示成如下形式:

其中

代表的自回归阶数.
代表的移动平均阶数.

Remark ARCH/GARCH随机过程产生的数据是什么样的? 前面提到它们允许样本的方差随时间变化, 但是由于必须满足平稳性(前提假设), 因此样本的方差从局部看是变化(震荡)的, 但从整体看应该是"平稳的"序列. 例如下图是一个过程生成的时间序列().

VAR(p)

VAR即Vector Autoregression, 它是多变量的自回归模型. 类似地, 我们有, 它是的向量版本. 需要注意的是, VARMA模型处理的时间序列可以有趋势. 我们不做详细的展开, 感兴趣的读者可以参考^[4]章节11.2: Vector Autoregressive models VAR(p) models.

4. 参数选择

给定时间序列的观测样本, 选定预测模型之后如何确定模型的参数? 本节我们介绍两种常用的方法: 1. 画出ACF/PACF图, 然后观察出的值; 2. 通过计算相关的统计指标, 自动化地选择参数.

4.1 观察ACF/PACF

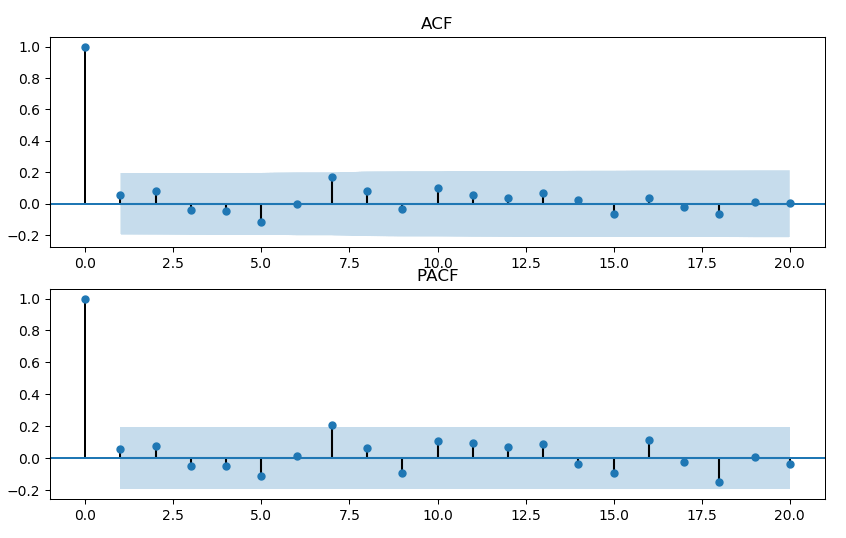
ACF

ACF的全称是Autocorrelation Function. 对变量, ACF的值代表与之间的相关性.

PACF

PACF的全称是Partial Autocorrelation Function. 对变量, PACF的值代表已知的条件下, 与之间的相关性.

例6 设. 考虑下面三个模型生成的时间序列, 并计算相应的ACF/PACF.

指导原则(参考^[4])

模型	ACF	PACF	说明
AR(p)	逐渐趋近于0或像正弦曲线一样收敛到0	前个值非常显著, 其余的值不显著	值主要参考PACF
MA(q)	前个值非常显著, 其余的值不显著	逐渐趋近于0或像正弦曲线一样收敛到0	值主要参考ACF
ARMA(p,q)	逐渐趋近于0或像正弦曲线一样收敛到0	逐渐趋近于0或像正弦曲线一样收敛到0	值靠猜

4.2 自动化地决定参数

基本思想是通过计算一些指标, 并选择参数使得相关的指标值尽可能小. 下面我们介绍一些常用的指标.

为方便描述, 我们先定义一些记号.

= 样本的大小
= 模型中需要拟合的参数数量(例如正态分布有的数量是2: 和)
= 通过最大似然估计得到的最大Likelihood

AIC(Akaike Information Criterion)^[7]

AICc^[8]

(AIC的改良版, 解决小样本过拟合的问题)

BIC(Bayesian Information Criterion)^[9]

(也称为Schwartz Criterion, SBC, SBIC)

HQIC(Hannan–Quinn Information Criterion)^[10]

Remark 建议在实际中综合考虑这些指标.

5. 实验代码

Python3 code on Github

参考文献

Wikipedia. Augmented Dickey-Fuller test. ↩
Dickey, D. A.; Fuller, W. A. Distribution of the Estimators for Autoregressive Time Series with a Unit Root. Journal of the American Statistical Association. 74(366): 427–431, 1979. ↩
https://www.statsmodels.org/dev/generated/statsmodels.tsa.stattools.adfuller.html ↩
Lecture notes of Applied Time Series Analysis (SATA 510). The Pennsylvania State University. ↩ ↩ ↩ ↩
Jan Grandell. Time series analysis (lecture notes). ↩
Bollerslev, T. Generalized autoregressive conditional heteroscedasticity. Journal of Econometrics, 31, 307–327, 1986. ↩
Hirotugu Akaike. A new look at the statistical model identification, IEEE Transactions on Automatic Control, 19 (6): 716–723, 1974. ↩
Wikipedia. https://en.wikipedia.org/wiki/Akaike_information_criterion#AICc. ↩
Schwartz E.S. The Stochastic Behavior of Commodity Prices: Implications for Valuation and Hedging'. J Finance 52(3) Papers and Proceedings Fifty-Seventh Annual Meeting, American Finance Association, New Orleans, Louisiana, 923-973, 1997. ↩
Hannan, E. J. and B. G. Quinn. The Determination of the order of an autoregression, Journal of the Royal Statistical Society, Series B, 41: 190–195, 1979. ↩