字节跳动2018年校招笔试题

1

思路

DFS 找出最大连通分量

代码

mat = []
mark = []

mn = input().split(',')
m = int(mn[0])
n = int(mn[1])

direction = [(-1, -1), (-1, 0), (-1, 1), (0, -1), (0, 1), (1, -1), (1, 0), (1, 1)]

def valid_pos(row, col):
	return row >= 0 and row < m and col >= 0 and col < n

for i in range(m):
	mat.append([int(x) for x in input().split(',')])
	mark.append([])
	for j in range(n):
		mark[i].append(False)

current_count = 0
max_count = 0
group_count = 0

def dfs(row, col):
	global current_count
	mark[row][col] = True
	current_count += 1
	for di in direction:
		new_row = row + di[0]
		new_col = col + di[1]
		if not valid_pos(new_row, new_col) or mark[new_row][new_col] or mat[new_row][new_col] == 0:
			continue
		dfs(new_row, new_col)

for row in range(m):
	for col in range(n):
		if mat[row][col] == 1 and not mark[row][col]:
			dfs(row, col)
			group_count += 1
			max_count = max(max_count, current_count)
			current_count = 0

print('%d,%d' % (group_count, max_count))

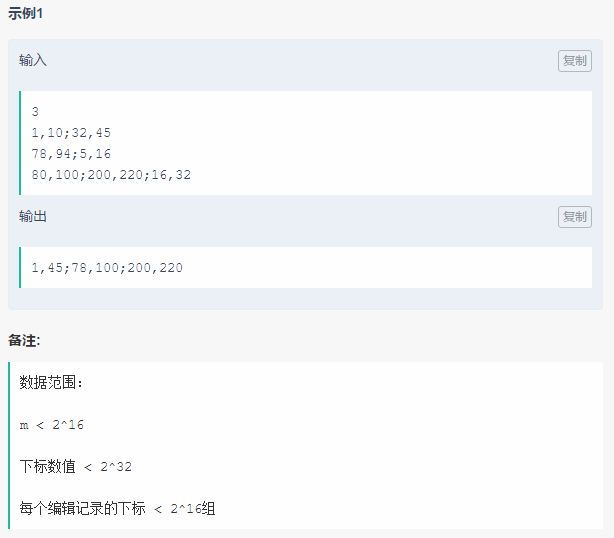
2

思路

先将所有输入都放入一个数组, 每个元素是一个二元组, 然后排序 (Python 默认按照二元组的字典序排序)
然后维护两个指针, 分别指向一个前一个区间$a$和后一个待合并的区间$b$, 如果
$a[1]>b[0]$
那么两个区间就合并, 新合并的区间为
$(a[0],max(a[1],b[1]))$
并将被合并的区间删除

代码

m = int(input())

array = []
for _ in range(m):
	for i in input().split(';'):
		span = i.split(',')
		array.append((int(span[0]), int(span[1])))
array.sort()

current = 0
for i in range(1, len(array)):
	if array[current][1] < array[i][0]:
		current = i
	else:
		array[current] = (array[current][0], max(array[current][1], array[i][1]))
		array[i] = None

res = []
for i in array:
	if i == None:
		continue
	res.append('%d,%d' % i)

print(';'.join(res))

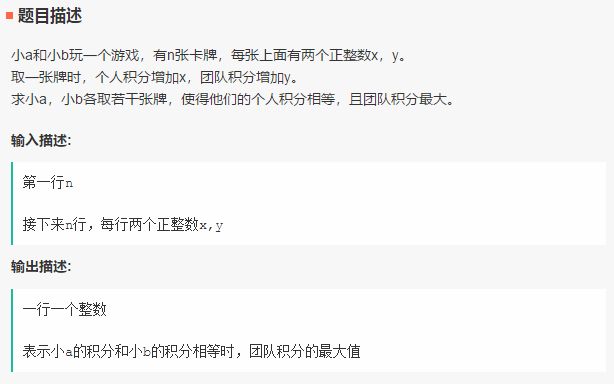
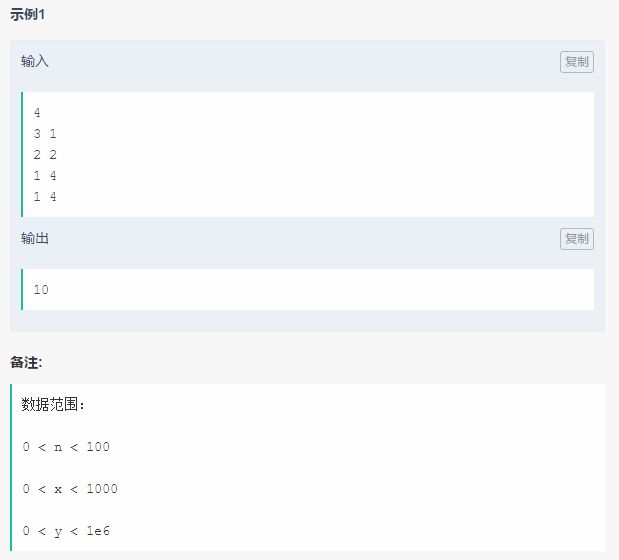
3

思路

之前的想法是回溯法+剪枝, 看了答案才发现是动态规划… 好难啊
$dp[i][j]$ 表示的是前 i 张牌, 积分相差为 j 的时候的最大团队积分
转移公式为 $dp[i][j]=max(dp[i-1][j],dp[i-1][j-person[i]]+team[i],dp[i-1][j+person[i]]+team[i])$

#include 
#define MAXN 100000
int dp[101][MAXN];
int person[101];
int team[101];

int max(int a, int b) {
	return (a > b) ? a : b;
}

int main() {
	for (int i = 0; i < 101; i++) {
		for (int j = 0; j < MAXN; j++) {
			dp[i][j] = -1;
		}
	}
	dp[0][0] = 0;
	int n;
	scanf("%d", &n);
	for (int i = 0; i < n; i++) {
		scanf("%d %d", person + i, team + i);
	}

	for (int i = 1; i <= n; i++) {
		for (int j = 0; j < MAXN; j++) {
			int p = person[i-1];
			int t = team[i-1];
			int a = ((j >= p) && (dp[i-1][j-p] != -1)) ? dp[i-1][j-p] + t : -1;
			int b = (((j + p) < MAXN) && (dp[i-1][j+p] != -1)) ? dp[i-1][j+p] + t : -1;
			dp[i][j] = max(max(a, b), dp[i-1][j]);
		}
	}

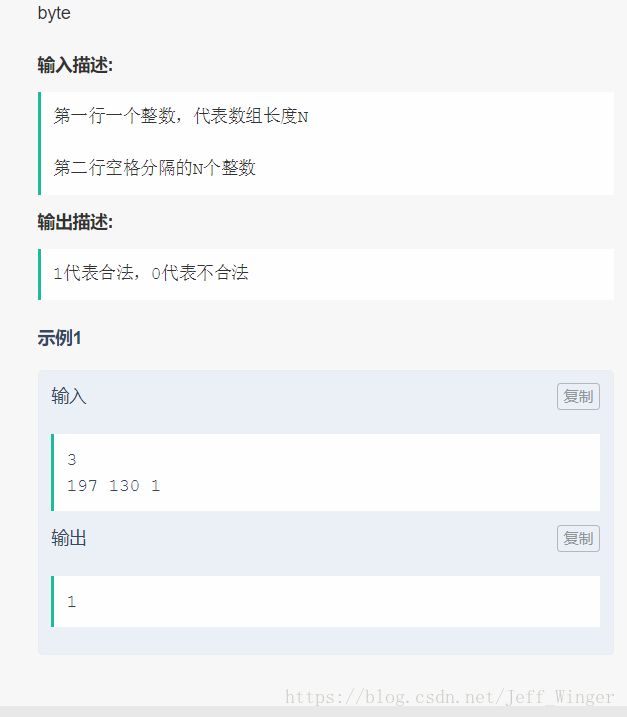
	printf("%d", dp[n][0]);
}

4

思路

送分题

代码

#include 
#include 

int n;
int* a;

int check() {
	for (int i = 0; i < n; i++) {
		int first = a[i];
		int length = 0;
		if ((first & 0x80) == 0) {
			length = 1;
		} else {
			while (first & 0x80) {
				length++;
				first = first << 1;
			}
			if (length > 4) return 0;
			if (length == 1) return 0;
			if ((i + length) > n) return 0;

			for (int j = 1; j < length; j++) {
				if ((a[i+j] & 0xe0) != 0x80) {
					return 0;
				}
			} 
			i += length - 1;
		}
	}
	return 1;
}

int main() {
	scanf("%d", &n);
	a = malloc(sizeof(int) * n);
	for (int i = 0; i < n; i++) {
		scanf("%d", a + i);
	}
	if (check()) {
		printf("1\n");
	} else {
		printf("0\n");
	}
}