KdTree理解与实现（Java）

抛出问题

如果让你设计一个外卖系统，你的数据库中有所有外卖商家所在的经纬度，那么如何能有效地根据用户的位置筛选出所有附近的商家？

最直接的方法是根据城市或者城市的每个区（如崂山区，市南区…）来对商家进行分类，然后根据用户所在的区返回同一区域下的所有商家。这个方法可以解决大部分问题，但是如果用户位于两个区的分界线周围怎么办？

KdTree简介

KdTree 是以二叉搜索树（Binary Search Tree）为原型的用于空间检索的数据结构，能够在随机分布的空间内以 O(log₂N) 的时间复杂度实现对平面内点的搜索以及 O(log₂N) + R 的复杂度查询平面内任意矩形内的所有点（R为矩形内点的个数）。 KdTree的应用十分广泛，包括且不限于范围搜索，最邻近点搜索，物理引擎中的碰撞检测以及地理节点（如外卖商家）数据库等。

原理简介

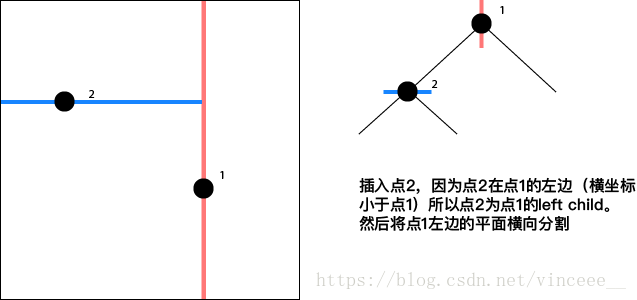
KdTree的实现方法与BST十分相似，以最常用的二维平面的KdTree为例，其每个节点存储一个二维的坐标点，并将平面空间以该点所在的横线/竖线递归地分割成两个子空间。
以width = 1.0, height = 1.0的单位平面为例，依次插入下列点

Note:

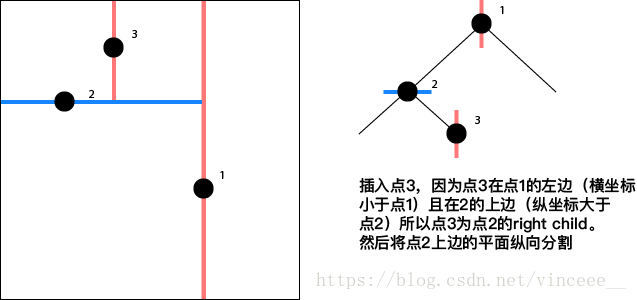
1. 点对平面的分割方式是横向/纵向按照层次交替出现（根节点是哪个方向都可以）。
2. 插入节点的方法类似于BST，即从根节点开始，（设要插入的节点为P_insert，当前遍历的节点为P_current）如果P_insert在P_current的左边或者下边，那么就访问P_current的left child， 反之访问right child直到成为叶子节点。
3. 本KdTree不支持删除操作。

代码实现

在介绍KdTree实现之前先定义两个辅助类Point（用来表示点）和Rect（用来表示矩形）

Point.java

用来表示一个坐标点，在本博客的语境下只需要两个方法：计算与另一点的距离（以平方和的形式） 和 判断两点是否相等。

// @file Point.java
// @author 王成昊 
// @date 2018.10.14
public class Point {
	public final double x;
	public final double y;
	
	// Point类是 immutable datatype
	public Point(double x, double y) {
		this.x = x;
		this.y = y;
	}
	
	// 为了减少计算量，一般使用平方和来表示距离
	public double distanceSquareTo(Point that) {
		double dx = that.x - this.x;
		double dy = that.y - this.y;
		return dx * dx + dy * dy;
	}
	
	@Override
	public boolean equals(Object that) {
		if (this == that) return true;
		if (that == null) return false;
		if (that.getClass() != this.getClass()) return false;
		Point point = (Point) that;
		return (x == point.x) && (y == point.y);
	}
}

Rect.java

用来表示一个矩形，在本例中使用四个坐标值来表示一个矩形。需要的方法是 判断矩形是否包含一个点 和 计算矩形和某点的距离（平方和的形式）

// @file Rect.java
// @author 王成昊 
// @date 2018.10.14
public class Rect {
	// 分别表示左下顶点和右上顶点
	public final double minX;
	public final double minY;
	public final double maxX;
	public final double maxY;
	
	// Rect类是 immutable datatype
	public Rect(double x0, double y0, double x1, double y1) {
		minX = x0;
		minY = y0;
		maxX = x1;
		maxY = y1;
	}
	
	// 判断该点是否位于该矩形之内
	public boolean contains(Point point) {
		return (point.x >= minX) && (point.x <= maxX)
			&& (point.y >= minY) && (point.y <= maxY); 
	}

	// 计算矩形到某一点的最近距离（以平方和的形式）
	public double distanceSquareToPoint(Point point) {
		double dx = 0.0;
		double dy = 0.0;
		if (point.x < minX) dx = minX - point.x;
		else if (point.x > maxX) dx = point.x - maxX;
		if (point.y < minY) dy = minY - point.y;
		else if (point.y > maxY) dy = point.y - maxY;
		return dx * dx + dy * dy;
	}
}

KdTree.java

本例中KdTree将实现4个功能：

• 插入
• 判断是否包含某点
• 查询任意矩形内的所有点
• 查询距离某一点最近的点

// @file KdTree.java
// @author 王成昊 
// @date 2018.10.14

import java.util.LinkedList;

public class KdTree {

    // 节点类，其中 rect 成员表示该节点所分割的平面，
    // 即它的左右孩子所表示的空间之和，该成员用于判断
    // 最邻近点
    private class Node {
        Point point;
        Rect rect;
        Node left;
        Node right;
        Node (Point p, Rect r) {
            point = p;
            rect = r;
            left = null;
            right = null;
        }
    }
    
    // 根节点
    private Node root;
    
    // 构造函数
    public KdTree() {
        root = null;
    }
    
    // 插入， 用同名私有方法递归实现， 默认根节点是纵向分割
    public void insert(Point point) {
        root = insert(point, root, false, 0.0, 0.0, 1.0, 1.0);
    }
    
    private Node insert(Point point, Node node, boolean isVertical, 
        double x0, double y0, double x1, double y1) {

        if (node == null) {
            return new Node(point, new Rect(x0, y0, x1, y1));
        }

        // 改变分割方向
        isVertical = !isVertical;

        // 判断要插入的点在当前点的左/下还是右/上
        double value0 = isVertical ? point.x : point.y;
        double value1 = isVertical ? node.point.x : node.point.y;
        if (value0 < value1) {
            node.left = insert(point, node.left, isVertical,
            x0, y0, isVertical ? node.point.x : x1, isVertical ? y1 : node.point.y);
        } else {
            node.right = insert(point, node.right, isVertical,
            isVertical ? node.point.x : x0, isVertical ? y0 : node.point.y, x1, y1);
        }
        return node;
    }
    
    // 判断是否包含该点， 用同名私有方法递归实现
    public boolean contains(Point point) {
        return contains(point, root, false);
    }

    private boolean contains(Point point, Node node, boolean isVertical) {
        if (node == null) return false;

        if (node.point.equals(point)) return true;

        // 改变分割方向
        isVertical = !isVertical;

        // 判断要查询的点在当前点的左/下还是右/上
        double value1 = isVertical ? point.x : point.y;
        double value2 = isVertical ? node.point.x : node.point.y;
        if (value1 < value2) {
            return contains(point, node.left, isVertical);
        } else {
            return contains(point, node.right, isVertical);
        }
    }

    // 返回矩形范围内的所有点， 用同名私有方法递归实现
    public Iterable<Point> range(Rect rect) {
        LinkedList<Point> result = new LinkedList<Point>();
        range(rect, root, false, result);
        return result;
    }

    private void range(Rect rect, Node node, boolean isVertical, LinkedList<Point> bag) {
        if (node == null) return;

        // 改变分割方向
        isVertical = !isVertical;
        Point point = node.point;
        if (rect.contains(point)) bag.add(point);

        // 判断当前点所分割的两个空间是否与矩形相交
        double value = isVertical ? point.x : point.y;
        double min = isVertical ? rect.minX : rect.minY;
        double max = isVertical ? rect.maxX : rect.maxY;
        if (min < value) {
            range(rect, node.left, isVertical, bag);
        }
        if (max >= value) {
            range(rect, node.right, isVertical, bag);
        }
    }

    // 返回距离该点最近的点， 用同名私有方法递归实现
    public Point nearest(Point target) {
        return nearest(target, root, null, false);
    }

    private Point nearest(Point target, Node node, Point currentBest, boolean isVertical) {
        if (node == null) return currentBest;
        isVertical = !isVertical;
        double value1 = isVertical ? target.x : target.y;
        double value2 = isVertical ? node.point.x : node.point.y;

        // 继续搜索目标点所在的半区
        Node next = value1 < value2 ? node.left : node.right;
        Node other = value1 < value2 ? node.right : node.left;
        Point nextBest = nearest(target, next, node.point, isVertical);
        double currentDistance = 0;
        double nextDistance = nextBest.distanceSquareTo(target);
        if (currentBest == null) {
            currentBest = nextBest;
            currentDistance = nextDistance;
        } else {
            currentDistance = currentBest.distanceSquareTo(target);
            if (nextDistance < currentDistance) {
                currentBest = nextBest;
                currentDistance = nextDistance;
            }
        }
        // 判断另一半区是否可能包含更近的点
        if ((other != null) && (other.rect.distanceSquareToPoint(target) < currentDistance)) {
            currentBest = nearest(target, other, currentBest, isVertical);
        }
        return currentBest;
    }
    public static void main(String[] args) {
		// unit test
    }
}

Note:
比较难理解的是nearest()方法，该方法为深度优先搜索，逻辑是：

1.从根节点开始向下搜索，递归搜索优势半区 （定义 目标点 为

public Point nearest(Point target)

中的target, 目标点所在的半区为优势半区，另一半区为劣势半区 ） ，并将当前点作为currentBest 参数传递给下层，直到叶子节点。

2.此时开始回溯，返回 nextBest ，获得 {该节点优势半区中的所有点，以及parent点} 中距离目标点最近的点 ，其最优距离为currentDistance。 此时考虑是否需要搜索劣势半区。

3.如果劣势半区所在的矩形与目标点的距离小于currentDistance，则搜索劣势半区。换句话说，如果矩形到目标点的距离小于currentDistance，说明劣势半区中有存在更近的点的可能。

复杂度比较

KdTree在最坏情况下的复杂度与暴力求解（用集合遍历所有元素）一样都是O(n)， 但在随机分布的情况下可以达到O(log₂N)。
以下为两个数据结构在随机分布的空间中的算法复杂度 (其中R表示矩形范围内点的个数)

数据结构	insert()	contains()	range()	nearest()
Set	1	N/2	N	N
KdTree	log2N	log2N	log2N + R	log2N

结语

之前在学数据库的时候大作业是做一个类似饿了么的外卖网站，其中的一个难点是如何根据用户所在的位置检索出所有附近的商家。当时想了半天也想不出来怎么能有效的进行区间搜索，用的是暴力方法（因为是demo所以数据量很小），现在学到了KdTree之后真的是大彻大悟啊