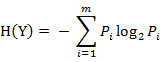特征选择
转载自 http://www.cnblogs.com/xiangshancuizhu/archive/2012/03/12/2392360.html
先看看博客上大家是怎么认为的吧:
如果用少量训练数据训练出来的模型(Ma)比使用全部数据但是经过特征裁剪训练出来的模型(Mb)性能还要高,那么能说明什么问题?这里面两个注意的地方,其一是少量数据产生的特征甚至还要比全部数据裁剪后的特征数量少很多,其二是如果用少量数据中的特征在全部数据上训练得到模型Mc,我猜测性能会比Mb更低。如果猜想成立,那么又说明了什么呢。
在自然语言处理中,我感觉特征中的term比template要重要很多,而事实上一个具体的特征又会由很多term合并而成。那么特征分组是否可以考虑以term为单位,尤其是衡量特征的有效性。特征选择(feature selection)是一种很有实用价值的技术,本质上来说是一种为数据挖掘消除数据噪声的技术。但我们对某件事务进行判断时,我们会根据以往的经验根据 某些信息,而不是所有的信息做出判断。比如,判断一辆车的品牌,我们会去看车头车尾的标志,更细致一点会去看车的铭牌,因为这是最权威,也是最容易判断车 辆品牌的信息。如果根据车的外形去判断车辆的品牌就有可能把QQ当作Spark,把F3当作花冠;如果根据车的价格去判断,也会把奥迪和大奔弄混。也就是说,人做判断时会选择出最有效的信息来做出自己的抉择。
计算机在面对类似问题的却无法根据已有的经验去选择最有效的信息,而大量无效信息对于计算机来说就是噪声,反而会影响计算机的判断结果。如果是前面对车辆品牌进行判断的例子,还可以人工的选择出最有效的信息。但是如果面对的是DNA序列、复杂的图片,那就只能依靠计算机了。于是这就诞生了特征选择技 术,选出与结果最相关的特征,从而提高判断的准确率。
http://www.zhizhihu.com/html/y2011/3188.html
特征选择是指从一组给定的特征集中,按照某一准则选择出一组具有良好区分特性的特征子集。特征选择又称独立评估法,在进行特征选择时一般都是利用某种评价函数独立地对每个原始特征项进行评分,然后将它们按分值的高低排序,从中选取若干个分值最高的特征项。
特征选择实际包含两个方面:特征提取和特征选择。特征提取是一种将数据从高维空间到低维空间的变换,达到降维的目的;特征选择是指从一组特征中去除冗余或不相关的特征来降维。两者常联合使用。
特征选择的作用主要是降低计算开销和提高分类性能。即可以减小数据处理量、节省处理时间,减轻数据中噪声的影响,提高信息处理系统的性能。
良好的特征集一般具有以下几个特点:可区分性、可靠性、独立性、数量少。
特征选择的基本方法为:先产生特征子集(选择算法),然后对子集进行评价(评价标准)。
特征子集的形成方法有:穷举法、启发法、随机法。
评价函数可分为:
筛选器(评价函数与分类器无关)
封装器(采用分类器的错误概率作为评价函数):距离测度、信息测度、相关性测度、一致性测度。
常见的特征提取方法有:主成分分析(PCA)、LDA(线性奇异分析)、独立分量分析(ICA)、神经网络、粗糙集属性约简等。而比较新的方法有:非线性降维方法、流形学习等,它们正成为特征选择的研究热点。
注:PCA与LDA的区别
PCA:非监督学习,把原始数据作为一类,使数据尽可能分开
LDA:有监督学习,已知两类数据的类别,使该两类尽可能分开
http://www.cnblogs.com/heaad/archive/2011/01/02/1924088.html
特征选择是指从一组给定的特征集中,按照某一准则选择出一组具有良好区分特性的特征子集。特征选择又称独立评估法,在进行特征选择时一般都是利用某种评价函数独立地对每个原始特征项进行评分,然后将它们按分值的高低排序,从中选取若干个分值最高的特征项。
特征选择实际包含两个方面:特征提取和特征选择。特征提取是一种将数据从高维空间到低维空间的变换,达到降维的目的;特征选择是指从一组特征中去除冗余或不相关的特征来降维。两者常联合使用。
特征选择的作用主要是降低计算开销和提高分类性能。即可以减小数据处理量、节省处理时间,减轻数据中噪声的影响,提高信息处理系统的性能。
良好的特征集一般具有以下几个特点:可区分性、可靠性、独立性、数量少。
特征选择的基本方法为:先产生特征子集(选择算法),然后对子集进行评价(评价标准)。
特征子集的形成方法有:穷举法、启发法、随机法。
评价函数可分为:
筛选器(评价函数与分类器无关)
封装器(采用分类器的错误概率作为评价函数):距离测度、信息测度、相关性测度、一致性测度。
常见的特征提取方法有:主成分分析(PCA)、LDA(线性奇异分析)、独立分量分析(ICA)、神经网络、粗糙集属性约简等。而比较新的方法有:非线性降维方法、流形学习等,它们正成为特征选择的研究热点。
注:PCA与LDA的区别
PCA:非监督学习,把原始数据作为一类,使数据尽可能分开
LDA:有监督学习,已知两类数据的类别,使该两类尽可能分开
(1) 什么是特征选择
特征选择 ( Feature Selection )也称特征子集选择( Feature Subset Selection , FSS ) ,或属性选择( Attribute Selection ) ,是指从全部特征中选取一个特征子集,使构造出来的模型更好。
(2) 为什么要做特征选择
在机器学习的实际应用中,特征数量往往较多,其中可能存在不相关的特征,特征之间也可能存在相互依赖,容易导致如下的后果:
Ø 特征个数越多,分析特征、训练模型所需的时间就越长。
Ø 特征个数越多,容易引起“维度灾难”,模型也会越复杂,其推广能力会下降。
特征选择能剔除不相关(irrelevant)或亢余(redundant )的特征,从而达到减少特征个数,提高模型精确度,减少运行时间的目的。另一方面,选取出真正相关的特征简化了模型,使研究人员易于理解数据产生的过程。
2 特征选择过程
2.1 特征选择的一般过程
特征选择的一般过程可用图1表示。首先从特征全集中产生出一个特征子集,然后用评价函数对该特征子集进行评价,评价的结果与停止准则进行比较,若评价结果比停止准则好就停止,否则就继续产生下一组特征子集,继续进行特征选择。选出来的特征子集一般还要验证其有效性。
综上所述,特征选择过程一般包括产生过程,评价函数,停止准则,验证过程,这4个部分。
(1) 产生过程( Generation Procedure )
产生过程是搜索特征子集的过程,负责为评价函数提供特征子集。搜索特征子集的过程有多种,将在2.2小节展开介绍。
(2) 评价函数( Evaluation Function )
评价函数是评价一个特征子集好坏程度的一个准则。评价函数将在2.3小节展开介绍。
(3) 停止准则( Stopping Criterion )
停止准则是与评价函数相关的,一般是一个阈值,当评价函数值达到这个阈值后就可停止搜索。
(4) 验证过程( Validation Procedure )
在验证数据集上验证选出来的特征子集的有效性。
图1. 特征选择的过程 ( M. Dash and H. Liu 1997 )
2.2 产生过程
产生过程是搜索特征子空间的过程。搜索的算法分为完全搜索(Complete),启发式搜索(Heuristic),随机搜索(Random) 3大类,如图2所示。
图2. 产生过程算法分类 ( M. Dash and H. Liu 1997 )
下面对常见的搜索算法进行简单介绍。
2.2.1完全搜索
完全搜索分为穷举搜索(Exhaustive)与非穷举搜索(Non-Exhaustive)两类。
(1) 广度优先搜索( Breadth First Search )
算法描述:广度优先遍历特征子空间。
算法评价:枚举了所有的特征组合,属于穷举搜索,时间复杂度是O(2n),实用性不高。
(2)分支限界搜索( Branch and Bound )
算法描述:在穷举搜索的基础上加入分支限界。例如:若断定某些分支不可能搜索出比当前找到的最优解更优的解,则可以剪掉这些分支。
(3) 定向搜索 (Beam Search )
算法描述:首先选择N个得分最高的特征作为特征子集,将其加入一个限制最大长度的优先队列,每次从队列中取出得分最高的子集,然后穷举向该子集加入1个特征后产生的所有特征集,将这些特征集加入队列。
(4) 最优优先搜索 ( Best First Search )
算法描述:与定向搜索类似,唯一的不同点是不限制优先队列的长度。
2.2.2 启发式搜索
(1)序列前向选择( SFS , Sequential Forward Selection )
算法描述:特征子集X从空集开始,每次选择一个特征x加入特征子集X,使得特征函数J( X)最优。简单说就是,每次都选择一个使得评价函数的取值达到最优的特征加入,其实就是一种简单的贪心算法。
算法评价:缺点是只能加入特征而不能去除特征。例如:特征A完全依赖于特征B与C,可以认为如果加入了特征B与C则A就是多余的。假设序列前向选择算法首先将A加入特征集,然后又将B与C加入,那么特征子集中就包含了多余的特征A。
(2)序列后向选择( SBS , Sequential Backward Selection )
算法描述:从特征全集O开始,每次从特征集O中剔除一个特征x,使得剔除特征x后评价函数值达到最优。
算法评价:序列后向选择与序列前向选择正好相反,它的缺点是特征只能去除不能加入。
另外,SFS与SBS都属于贪心算法,容易陷入局部最优值。
(3) 双向搜索( BDS , Bidirectional Search )
算法描述:使用序列前向选择(SFS)从空集开始,同时使用序列后向选择(SBS)从全集开始搜索,当两者搜索到一个相同的特征子集C时停止搜索。
双向搜索的出发点是 ![]() 。如下图所示,O点代表搜索起点,A点代表搜索目标。灰色的圆代表单向搜索可能的搜索范围,绿色的2个圆表示某次双向搜索的搜索范围,容易证明绿色的面积必定要比灰色的要小。
。如下图所示,O点代表搜索起点,A点代表搜索目标。灰色的圆代表单向搜索可能的搜索范围,绿色的2个圆表示某次双向搜索的搜索范围,容易证明绿色的面积必定要比灰色的要小。
图2. 双向搜索
(4) 增L去R选择算法 ( LRS , Plus-L Minus-R Selection )
该算法有两种形式:
<1> 算法从空集开始,每轮先加入L个特征,然后从中去除R个特征,使得评价函数值最优。( L > R )
<2> 算法从全集开始,每轮先去除R个特征,然后加入L个特征,使得评价函数值最优。( L < R )
算法评价:增L去R选择算法结合了序列前向选择与序列后向选择思想, L与R的选择是算法的关键。
(5) 序列浮动选择( Sequential Floating Selection )
算法描述:序列浮动选择由增L去R选择算法发展而来,该算法与增L去R选择算法的不同之处在于:序列浮动选择的L与R不是固定的,而是“浮动”的,也就是会变化的。
序列浮动选择根据搜索方向的不同,有以下两种变种。
<1>序列浮动前向选择( SFFS , Sequential Floating Forward Selection )
算法描述:从空集开始,每轮在未选择的特征中选择一个子集x,使加入子集x后评价函数达到最优,然后在已选择的特征中选择子集z,使剔除子集z后评价函数达到最优。
<2>序列浮动后向选择( SFBS , Sequential Floating Backward Selection )
算法描述:与SFFS类似,不同之处在于SFBS是从全集开始,每轮先剔除特征,然后加入特征。
算法评价:序列浮动选择结合了序列前向选择、序列后向选择、增L去R选择的特点,并弥补了它们的缺点。
(6) 决策树( Decision Tree Method , DTM)
算法描述:在训练样本集上运行C4.5或其他决策树生成算法,待决策树充分生长后,再在树上运行剪枝算法。则最终决策树各分支处的特征就是选出来的特征子集了。决策树方法一般使用信息增益作为评价函数。
2.2.3 随机算法
(1) 随机产生序列选择算法(RGSS, Random Generation plus Sequential Selection)
算法描述:随机产生一个特征子集,然后在该子集上执行SFS与SBS算法。
算法评价:可作为SFS与SBS的补充,用于跳出局部最优值。
(2) 模拟退火算法( SA, Simulated Annealing )
模拟退火算法可参考 大白话解析模拟退火算法 。
算法评价:模拟退火一定程度克服了序列搜索算法容易陷入局部最优值的缺点,但是若最优解的区域太小(如所谓的“高尔夫球洞”地形),则模拟退火难以求解。
(3) 遗传算法( GA, Genetic Algorithms )
遗传算法可参考 遗传算法入门 。
算法描述:首先随机产生一批特征子集,并用评价函数给这些特征子集评分,然后通过交叉、突变等操作繁殖出下一代的特征子集,并且评分越高的特征子集被选中参加繁殖的概率越高。这样经过N代的繁殖和优胜劣汰后,种群中就可能产生了评价函数值最高的特征子集。
随机算法的共同缺点:依赖于随机因素,有实验结果难以重现。
2.3 评价函数
评价函数的作用是评价产生过程所提供的特征子集的好坏。
评价函数根据其工作原理,主要分为筛选器(Filter)、封装器( Wrapper )两大类。
筛选器通过分析特征子集内部的特点来衡量其好坏。筛选器一般用作预处理,与分类器的选择无关。筛选器的原理如下图3:
图3. Filter原理(Ricardo Gutierrez-Osuna 2008 )
封装器实质上是一个分类器,封装器用选取的特征子集对样本集进行分类,分类的精度作为衡量特征子集好坏的标准。封装器的原理如图4所示。
图4. Wrapper原理 (Ricardo Gutierrez-Osuna 2008 )
下面简单介绍常见的评价函数。
(1) 相关性( Correlation)
运用相关性来度量特征子集的好坏是基于这样一个假设:好的特征子集所包含的特征应该是与分类的相关度较高(相关度高),而特征之间相关度较低的(亢余度低)。
可以使用线性相关系数(correlation coefficient) 来衡量向量之间线性相关度。
( 2) 距离 (Distance Metrics )
运用距离度量进行特征选择是基于这样的假设:好的特征子集应该使得属于同一类的样本距离尽可能小,属于不同类的样本之间的距离尽可能远。
常用的距离度量(相似性度量)包括欧氏距离、标准化欧氏距离、马氏距离等。
(3) 信息增益( Information Gain )
假设存在离散变量Y,Y中的取值包括{y1,y2,....,ym} ,yi出现的概率为Pi。则Y的信息熵定义为:
信息熵有如下特性:若集合Y的元素分布越“纯”,则其信息熵越小;若Y分布越“紊乱”,则其信息熵越大。在极端的情况下:若Y只能取一个值,即P1=1,则H(Y)取最小值0;反之若各种取值出现的概率都相等,即都是1/m,则H(Y)取最大值log2m。
在附加条件另一个变量X,而且知道X=xi后,Y的条件信息熵(Conditional Entropy)表示为:
在加入条件X前后的Y的信息增益定义为
![]()
类似的,分类标记C的信息熵H( C )可表示为:
将特征Fj用于分类后的分类C的条件信息熵H( C | Fj )表示为:
选用特征Fj前后的C的信息熵的变化成为C的信息增益(Information Gain),用![]() 表示,公式为:
表示,公式为:
假设存在特征子集A和特征子集B,分类变量为C,若IG( C|A ) > IG( C|B ) ,则认为选用特征子集A的分类结果比B好,因此倾向于选用特征子集A。
(4)一致性( Consistency )
若样本1与样本2属于不同的分类,但在特征A、 B上的取值完全一样,那么特征子集{A,B}不应该选作最终的特征集。
(5)分类器错误率 (Classifier error rate )
使用特定的分类器,用给定的特征子集对样本集进行分类,用分类的精度来衡量特征子集的好坏。
以上5种度量方法中,相关性、距离、信息增益、一致性属于筛选器,而分类器错误率属于封装器。
筛选器由于与具体的分类算法无关,因此其在不同的分类算法之间的推广能力较强,而且计算量也较小。而封装器由于在评价的过程中应用了具体的分类算法进行分类,因此其推广到其他分类算法的效果可能较差,而且计算量也较大。