PRML 学习: (1) Polynomial Curve Fitting
多项式曲线拟合是比较基础的回归分析方法,假设有一独立变量 x x x 和与其相关的变量 y y y,存在着变量 x x x 的 m m m 阶多项式可以模拟这种映射关系,可以用于解决一些非线性拟合问题。
1 基础概念
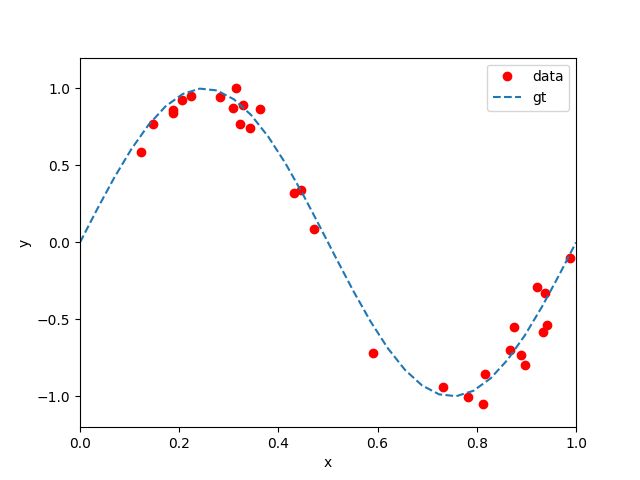
给定一组包含 n n n 个观测数据 x x x, x = { x 0 , x 1 , … , x n } \mathbf{x} = \{ x_0, x_1, \dots, x_n \} x={x0,x1,…,xn},和其对应的预测值 y y y, y = { y 0 , y 1 , … , y n } \mathbf{y} = \{ y_0, y_1, \dots, y_n \} y={y0,y1,…,yn}, 例如图1中利用 s i n ( 2 π x ) sin(2\pi x) sin(2πx) 函数合成的观测数据(30组加入了随机均匀噪声的观测值)。我们的目标就是使用这样的一个观测数据,训练/学习到一个模型,当引入新的数值 x ^ \hat{x} x^ 时,可以有效得预测它对应的数值 y ^ \hat{y} y^ 。
可以看出,实现这一目标暗示着,我们要尽可能地找到观测数据所对应的潜在的模型,即 s i n ( 2 π x ) sin(2\pi x) sin(2πx) 。 但是要通过有限的观测数据(含有噪声)准确地泛化出这一模型,是相当困难的。即便如此,我们还是可以把这一问题简化成为曲线拟合问题。我们指定采用的多项式形式为:
(1) y ( x , w ) = w 0 + w 1 x + w 2 ∗ x 2 + ⋯ + w m x m = ∑ i = 0 m w i x i , y(x, \mathbf{w}) = w_0 + w_1x + w_2*x^2 + \dots + w_mx^m = \sum_{i=0}^{m}w_ix^i, \tag{1} y(x,w)=w0+w1x+w2∗x2+⋯+wmxm=i=0∑mwixi,(1)
其中,取 x x x 幂次最高值 m m m, 称该多项式为 m m m 次多项式。虽然,该多项式是 x x x 的非线性函数,但是却是待系数 w \mathbf{w} w 的线性方程。方程 ( 1 ) (1) (1) 的矩阵形式为:
(2) Y = X w , \mathcal{\pmb{Y}} = \mathcal{\pmb{X}} \mathbf{w}, \tag{2} YYY=XXXw,(2)
其中,
Y = [ y 0 y 1 ⋮ y n ] , \mathcal{\pmb{Y}} = \left[ \begin{matrix} y_{0} \\ y_{1} \\ \vdots\\ y_{n} \end{matrix}\right] , YYY=⎣⎢⎢⎢⎡y0y1⋮yn⎦⎥⎥⎥⎤,
X = [ 1 x 0 x 0 2 … x 0 m 1 x 1 x 1 2 … x 1 m ⋮ 1 x n x n 2 … x n m ] , \mathcal{\pmb{X}} = \left[ \begin{matrix} 1 & x_0 & x_0^2 \dots & x_0^m \\ 1 & x_1 & x_1^2 \dots & x_1^m \\ & & \vdots & \\ 1 & x_n & x_n^2 \dots & x_n^m \\ \end{matrix}\right] , XXX=⎣⎢⎢⎢⎡111x0x1xnx02…x12…⋮xn2…x0mx1mxnm⎦⎥⎥⎥⎤,
w = [ w 0 w 1 ⋮ w n ] \mathbf{w} = \left[ \begin{matrix} w_{0} \\ w_{1} \\ \vdots\\ w_{n} \end{matrix}\right] w=⎣⎢⎢⎢⎡w0w1⋮wn⎦⎥⎥⎥⎤
通过观测数据就可以确定该多项式的系数,假设我们已经得到了这样一组系数 w \mathbf{w} w,那么理想的情况下,我们当然希望对于给定的任一观测值,由模型计算提供的预测值尽可能的接近对应的观测数据,即残差平方和误差函数( Residual sum of squares (RSS), or the sum of squared residuals (SSR), or the sum of squared errors of prediction (SSE)):
(3) L ( w ) = 1 2 ∑ i = 1 n { y ( x i , w ) − y i } 2 , \mathcal{L(\mathbf{w})} = \frac{1}{2}\sum_{i=1}^n \{ y(x_i, \mathbf{w}) - y_i\}^2, \tag{3} L(w)=21i=1∑n{y(xi,w)−yi}2,(3)
这里我们把由模型参数 w \mathbf{w} w 得到的估值 y ( x i , w ) y(x_i, \mathbf{w}) y(xi,w) 简记为 y ^ i \hat{y}_i y^i, 于是 ( 3 ) (3) (3) 就可以简化为: L ( w ) = 1 2 ∑ i = 1 n { y ^ i − y i } 2 \mathcal{L(\mathbf{w})} = \frac{1}{2}\sum_{i=1}^n \{ \hat{y}_i - y_i\}^2 L(w)=21∑i=1n{y^i−yi}2 , 公式 ( 3 ) (3) (3) 中的常数 1 2 \frac{1}{2} 21,主要是为了方便后面求解过程,当然即便不引入也没关系。
随着多项式模型的最高阶数 m m m 增大,我们可以想象,即便变量 x x x 有很小的变化, x m x^m xm 对这一变化也可能很敏感,也就是说模型的复杂度/非线性程度较大,在训练数据较少的时候,这很容易导致过拟合问题(over-fitting):
因此,一般会通过进入正则项(regularization)来限制模型复杂度,以提高泛化能力:
(4) L ( w ) = 1 2 ∑ i = 1 n { y ( x i , w ) − y i } 2 + λ 2 ∣ ∣ w ∣ ∣ 2 , \mathcal{L(\mathbf{w})} = \frac{1}{2}\sum_{i=1}^n \{ y(x_i, \mathbf{w}) - y_i\}^2 + \frac{\lambda}{2}||\mathbf{w}||^2, \tag{4} L(w)=21i=1∑n{y(xi,w)−yi}2+2λ∣∣w∣∣2,(4)
其中, ∣ ∣ w ∣ ∣ 2 = w T w = w 0 2 + w 1 2 + ⋯ + w m 2 ||\mathbf{w}||^2 = \mathbf{w}^T\mathbf{w} = w_0^2 + w_1^2 + \dots + w_m^2 ∣∣w∣∣2=wTw=w02+w12+⋯+wm2,参数 λ \lambda λ 控制 ∣ ∣ w ∣ ∣ 2 ||\mathbf{w}||^2 ∣∣w∣∣2 的大小从而影响模型的复杂度并且在一定程度上影响模型的过拟合程度,在神经网络中,这种方法也被称为 weight decay。可以看出,当 λ = 0 \lambda = 0 λ=0 时,方程 ( 4 ) (4) (4) 退化成 ( 3 ) (3) (3),参数 λ \lambda λ 的作用本质上来讲就是权衡模型的偏差 (Bias) 与方差 (Variance) ,亦称 Bias-variance tradeoff。有了 L ( w ) \mathcal{L(\mathbf{w})} L(w) 通常就很容易用均方根误差 ( root-mean-square error, RMS) 来衡量模型的泛化性能:
(5) E R M S = 2 ∗ L ( w ) / n , E_{RMS} = \sqrt{2*\mathcal{L}(\mathbf{w}) / n}, \tag{5} ERMS=2∗L(w)/n,(5)
###2 最小二乘解
对于方程 ( 4 ) (4) (4) 我们将其转为矩阵形式,可得:
(6) L ( w ) = 1 2 ( X w − Y ) T ( X w − Y ) + λ 2 w T w , \mathcal{L(\mathbf{w})} = \frac{1}{2}(\mathcal{\pmb{X}} \mathbf{w} - \mathcal{\pmb{Y}})^T(\mathcal{\pmb{X}} \mathbf{w} - \mathcal{\pmb{Y}}) + \frac{\lambda}{2}\mathbf{w}^T\mathbf{w}, \tag{6} L(w)=21(XXXw−YYY)T(XXXw−YYY)+2λwTw,(6)
很明显,这是一个关于 w \mathbf{w} w 的二次函数,则其一定存在唯一的极值点,而且对于曲线拟合问题,该极值点理论上应该就是最小值点,且该极值点满足:
(7) ∂ L ∂ w = ( X w − Y ) T X + λ w T = 0 , \frac{\partial \mathcal{L}}{\partial \mathbf{w}} = (\mathcal{\pmb{X}} \mathbf{w} - \mathcal{\pmb{Y}})^T\mathcal{\pmb{X}} + \lambda \mathbf{w}^T = 0, \tag{7} ∂w∂L=(XXXw−YYY)TXXX+λwT=0,(7)
即,
(8) w T ( X T X + λ I ) − Y T X = 0 , \mathbf{w}^T(\mathcal{\pmb{X}}^T \mathcal{\pmb{X}} + \lambda \mathbf{I} ) - \mathcal{\pmb{Y}}^T\mathcal{\pmb{X}} = 0, \tag{8} wT(XXXTXXX+λI)−YYYTXXX=0,(8)
即,
(9) w T = Y T X ( X T X + λ I ) − 1 , \mathbf{w}^T = \mathcal{\pmb{Y}}^T\mathcal{\pmb{X}}(\mathcal{\pmb{X}}^T \mathcal{\pmb{X}} + \lambda \mathbf{I} )^{-1}, \tag{9} wT=YYYTXXX(XXXTXXX+λI)−1,(9)
可得:
(10) w = ( ( X T X + λ I ) − 1 ) T X T Y , \mathbf{w} = ((\mathcal{\pmb{X}}^T \mathcal{\pmb{X}} + \lambda \mathbf{I} )^{-1})^T\mathcal{\pmb{X}}^T\mathcal{\pmb{Y}}, \tag{10} w=((XXXTXXX+λI)−1)TXXXTYYY,(10)
###3 实验结果
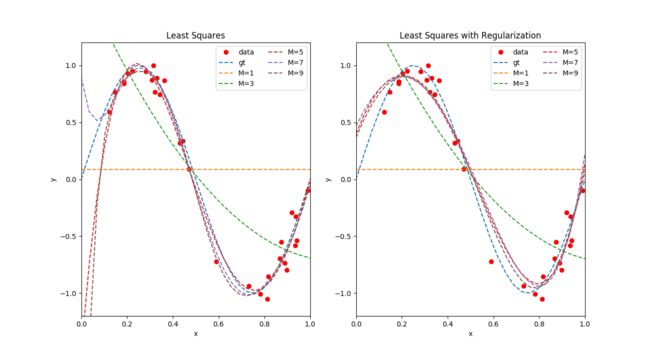
- 图 2 展示了两组使用最小二乘法拟合结果,其中左边的拟合不包含正则化项( λ = 0 \lambda = 0 λ=0),右边的包含正则化项( λ = 1 e − 3 \lambda = 1e-3 λ=1e−3), 分别绘制了多项式最高幂次 M = { 1 , 3 , 5 , 7 , 9 } M = \{1, 3, 5, 7, 9\} M={1,3,5,7,9} 的拟合曲线。
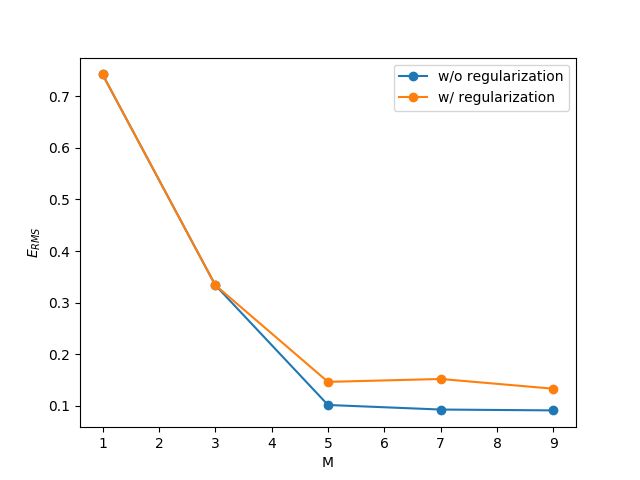
- 图 3 展示了不使用( w/o) / 使用 (w/) 正则化项对于 E R M S E_{RMS} ERMS 的影响(1.此处, λ = 1 e − 3 \lambda = 1e-3 λ=1e−3 ;2.对于使用正则化项的情形,我们只统计 1 2 ∑ i = 1 n { y ( x i , w ) − y i } 2 \frac{1}{2}\sum_{i=1}^n \{ y(x_i, \mathbf{w}) - y_i\}^2 21∑i=1n{y(xi,w)−yi}2 部分 )。可以看出,使用正则化项后,可以降低模型的复杂度,但是也会会导致 E R M S E_{RMS} ERMS 增大。
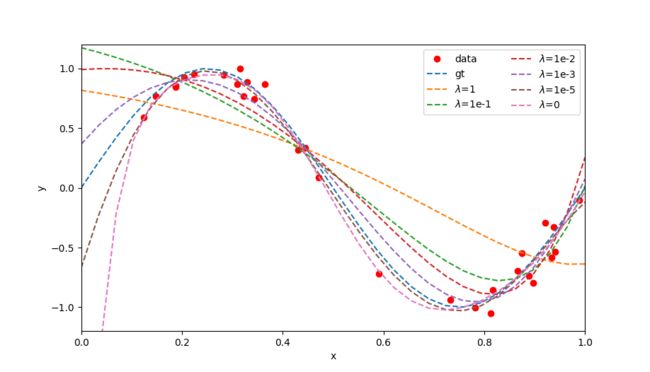
- 图 4 展示了不同 λ \lambda λ 值对于模型的影响,当 λ \lambda λ 值较大时模型复杂度较低,反之亦然。
References:
- Pattern Recognition and Machine Learning, Christopher M. Bishop
- Pattern Calssification, Richard O. Duda, et al.