数据结构—树与二叉树

总第119篇

前言

之前谈到的线性表、栈和队列都是一对一的数据结构，但是现实中也存在很多一对多的数据结构，这篇要写的就是一种一对多的数据结构———树。全文分为如下几部分：

• 树的一些基本概念

• 树的存储结构

• 二叉树

• 树与二叉树相互转换

• 树和森林的遍历

前文导航：

数据结构—线性表

数据结构-栈和队列

树的一些基本概念

树是n个结点的有限集，n=0时称为空树，在任意一颗非空树中：

• 有且只有一个特定的称为根的结点（下图中的结点A），

• 当n>1时，其余结点可分为m个互不相交的有限集T1、T2、……、Tm，其中每一个集合本身又是一棵树，并且称为根的子树。
  

  

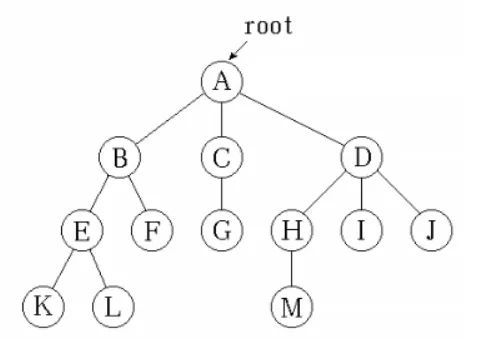
结点：A、B、C、D等都是结点，结点不仅包含数据元素，而且包含指向子树的分支。比如，结点A不仅包含数据元素A，还包含指向结点B、C、D的指针。

结点的度：结点拥有的子树个数或者分支的个数。例如，A结点有B、C、D3棵子树，所以A结点的的度为3。

树的深度或高度：树中各结点度的最大值称为树的深度。

结点的深度：结点的深度是从根结点到该结点路径上的结点个数。

结点的高度：从某一结点往下走可能到达的多个叶子结点，对应了多条通往这些叶子节点的路径，其中最长那条路径的长度即为该结点在树中的深度。根节点的高度为树的高度。
叶子结点：是指结点的度为0的结点，即不指向任何结点的结点。比如结点F、G、M、I、J。

孩子：某一结点指向的结点，比如A结点的孩子就是B、C、D结点。

双亲：与孩子相对应，B、C、D的双亲就是结点A。

兄弟：同一双亲的孩子之间互称为兄弟。B、C、D结点互称为兄弟。

堂兄弟：双亲在同一层次的结点互为堂兄弟。G、H、F互为堂兄弟。

祖先：从根结点到具体某节点的路径上的所有结点，都是这个结点的祖先。结点K的祖先是A、B、E。

子孙：与祖先的概念相对应，以某结点为根的子树中的所有结点，都是该结点的子孙。结点D的子孙为H、I、J、M。

层次：从根开始，根为第一层，根的孩子为第二层，根的孩子的孩子为第三层，以此类推。

无序树：如果将树中结点的各子树看成是从左至右是有次序的，不能互换的，则称该树为有序树，否则称为无序树。

森林：是若干颗互不相交的树的集合。如果把根节点A去掉，剩下的三棵互不相交树就是森林。

树的存储结构

1.顺序存储结构

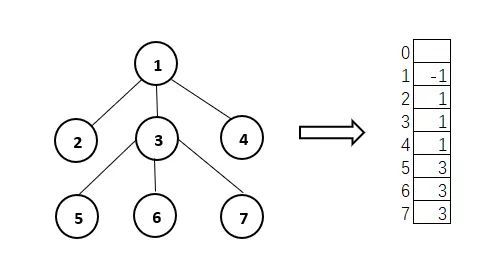
树的顺序存储结构中最简单直观的是双亲存储结构，用一维数组即可实现。双亲结点就是用双亲的信息来存储数据，比如结点2、3、4的双亲是1，结点5、6、7的双亲是3，结点1是根节点，无双亲，令其等于-1。

2.链式存储结构

树的链式存储中最常用的两种结构主要是孩子存储结构、孩子兄弟存储结构。

孩子存储结构就是让每个结点由一个数据域+若干个指针域组成，指针域的个数等于孩子的个数，让每个指针指向一个孩子。

孩子兄弟存储结构是每个结点有两个指针，一个指针指向该结点的其中一个孩子(长子)，另一个指针指向该结点的兄弟。

二叉树

二叉树是由n个结点的有限集合，该集合或者为空集，或者由一个根节点和两颗互不相交的、分别称为根节点的左子树和右子树的二叉树组成。

二叉树有如下特征：

• 每个结点最多只有两颗子树，即二叉树中结点的度最高不能超过2。

• 子树的左右顺序之分，不能颠倒。

1.特殊二叉树

满二叉树：在一颗二叉树中，如果所有的分支结点都有左孩子和右孩子结点，并且叶子节点都集中在二叉树的最下一层，则这样的二叉树称为满二叉树。

完全二叉树：如果对一颗深度为k，有n个结点的二叉树进行编号后，各结点的编号与深度为k的满二叉树中相同位置上的结点的编号均相同，那么这棵二叉树就是一颗完全二叉树。
一颗完全二叉树其实就是由一颗满二叉树从右至左从下至上的，挨个删除结点以后所得到的。

2.二叉树的存储结构

2.1顺序存储结构

顺序存储即用一个数组来存储一颗二叉树，具体存储方法为将二叉树中的结点进行编号，然后按编号依次将结点值存入到一个数组中，即完成了一颗二叉树的顺序存储。这种存储结构比较适合存储完全二叉树，用于存储一般的二叉树会浪费大量的存储空间。

2.2链式存储结构

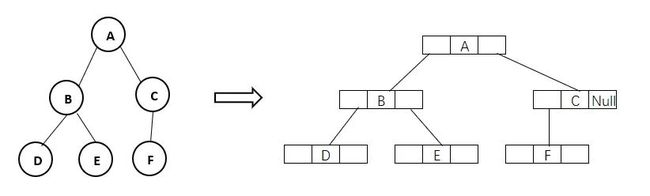
顺序结构有一定的局限性，不便于存储任意形态的二叉树。通过二叉树的形态，可以发现一个根节点与两颗子树有关系，因此设计一个含有一个数据域和两个指针域的链式结点结构，具体如下：

data表示数据域，用于存储对应的数据元素；lchild和rchild分别表示左指针域和右指针域，分别用于存储左孩子结点和右孩子结点的位置,如果没有右孩子结点，则右指针为空。这种存储结构称为二叉链表存储结构。定义如下：

typedef struct BTNode
{
    char data;
    struct BTNode *lchild;
    struct BTNode *rchild;
}BTNode;

3.二叉树的遍历

二叉树的遍历分为深度优先遍历和广度优先遍历，深度优先遍历主要就是先序、中序、后序这三种遍历方式，而层次遍历属于广度优先遍历。下面几种遍历的前提是树不为空，如果树为空，则停止遍历。

3.1先序遍历

先访问根节点，然后遍历左子树，最后遍历右子树。代码如下：

void preorder(BTNode *p)
{
    if(p != NULL)
    {
        Visit(p);    //Visit为访问函数，其中包含了对结点p的各种访问操作
        preorder(p -> lchild);    //遍历左子树
        preorder(p -> rchild);    //遍历右子树
    }
}

3.2中序遍历

先遍历左子树，然后访问根节点，最后遍历右子树。

void preorder(BTNode *p)
{
    if(p != NULL)
    {

        inorder(p -> lchild);    //遍历左子树
        Visit(p);    //访问根结点
        inorder(p -> rchild);    //遍历右子树
    }
}

3.3后序遍历

先遍历左子树，然后遍历右子树，最后访问根结点。

void preorder(BTNode *p)
{
    if(p != NULL)
    {

        posorder(p -> lchild);    //遍历左子树
        posorder(p -> rchild);    //遍历右子树
        Visit(p);    //访问根结点
    }
}

3.4层次遍历

层次遍历是将树分为若干层，然后每一层（互为兄弟的结点为一层）每一层去遍历。如下图所示：

具体代码如下：

void level(BTNode *p)
{
    int front,rear;
    BTNode *que[maxsize];
    front = rear = 0;
    BTNode *q;
    if(p != NULL)
    {
        rear = (rear + 1)%maxsize;
        que[rear] = p;
        while(front != rear)
        {
            front = (front + 1)%maxsize;
            q = que[front];
            Visit(q);
            if(q -> lchild != NULL)
            {
                rear = (rear +1)%maxsize;
                que[rear] = q -> lchild;
            }
            if(q -> rchild != NULL)
            {
            rear = (rear + 1)%maxsize;
            que[rear] = q -> rchild;
            }
        }
    }
}

树和森林与二叉树的相互转换

树的链式存储结构和二叉树存储结构的指针域表示的意义不同，在二叉树链式存储结构中，结点的左指针域指向左孩子，右指针域指向右孩子；而在树的链式存储中，结点的一个指针用来指向一个孩子，另一个指针用来指向自己的兄弟结点，我们把这种方式称为孩子兄弟存储法。

关于树、森林、二叉树之间的相互转化，这篇博客写的很清晰，很详细，这里直接引用该博主的文章。
博客地址：https://blog.csdn.net/u011240016/article/details/52823925

1.树转化为二叉树

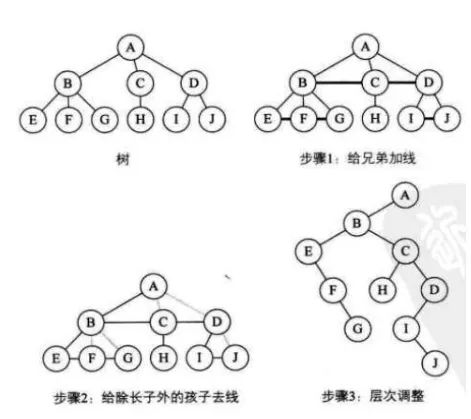
树变二叉树的规则：每个结点的左指针指向它的第一个孩子结点。右指针指向它在树中的相邻兄弟结点。也即：左孩子右兄弟。根没有兄弟，所以转换以后的树没有右子树。

具体操作：

• 在兄弟之间连线

• 对每一个结点，只保持它与第一个子结点（长子）的连线，与其他子结点的连线全部抹去。

• 以树根为轴心，顺时针旋转45度。
  

  

2.二叉树转化为树

二叉树转化为树这个过程是树转化为二叉树的一个逆过程，具体转化过程如下：

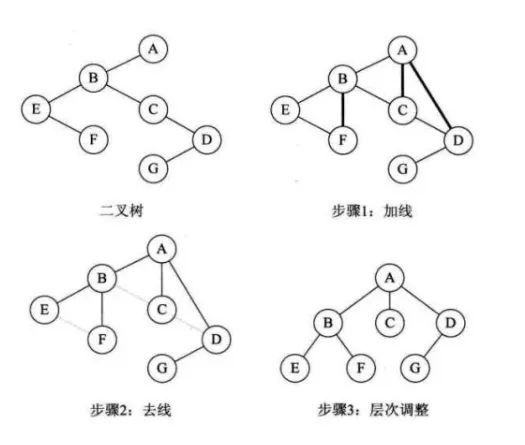
• 加线。如果某个结点有左孩子，那么把这个左孩子的右孩子，右孩子的右孩子，一直右下去，全部连接到这个结点。这个对应树变二叉树算法中的抹掉与长子以外的结点的连线，现在要找回自己的全部儿子。

• 去线。删除树中所有结点与这些右孩子的连线。找回了自己的儿子，不容许别人还和它们有瓜葛。

• 层次调整。
  

  

3.森林转化为二叉树

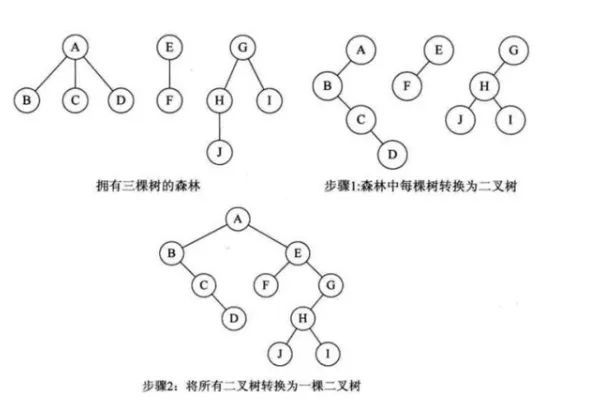
森林转化为二叉树的规则是:

• 先将每一棵树化为二叉树

• 第一棵树的根作为转换后的二叉树的根

• 第一棵树的左子树作为转换后的二叉树的根的左子树

• 第二棵树作为二叉树的右子树

• 第三棵树作为二叉树右子树的右子树
  …
  

  

这里主要运用的点是：转换为二叉树后，这个二叉树没有右子树，因此腾出右手可以接一棵新的树，因此这样可以连接很多由树化来的二叉树。

对照这个算法去想二叉树变森林，就很容易明白，先砍掉根和它的左子树作为一个整体，再对剩下的部分同样操作。

4.二叉树转化为森林

转化规则如下：

• 递归出口：若二叉树非空，则二叉树根及其左子树作为第一棵树的二叉树形式。

• 递归：操作二叉树的右子树。即拿掉一棵树后，再对剩下的二叉树部分进行同样的操作，直到无右子树为止。

砍成一堆二叉树后，还得注意并没结束，重点不是二叉树，而是树，因此用上面的二叉树化树的算法化成森林。

树和森林的遍历

1.树的遍历

树的遍历有两种方式：先序遍历和后序遍历。

先序遍历是先访问根结点，再依次访问根结点的每棵子树，访问子树时仍然遵循先根结点再子树的原则。

后序遍历是先依次访问根结点的每颗子树，再访问根结点，访问子树时仍然遵循先子树再根的规则。

2.森林的遍历

森林的遍历方式也有两种，一种是先序遍历、一种是后序遍历。

先序遍历的过程：先访问森林中第一颗树的根结点，然后先序遍历第一颗树中根结点的子树，最后先序遍历森林中除第一颗树以外的其他树。

后续遍历的过程：先后序遍历第一颗树中根结点的子树，然后访问第一颗树的根结点，最后后序遍历森林中除去第一颗树以外的森林。