算法分析与设计作业12：图的m着色问题

1.问题

图的m着色问题。给定无向连通图G和m种颜色，用这些颜色给图的顶点着色，每个顶点一种颜色。如果要求G的每条边的两个顶点着不同颜色。给出所有可能的着色方案;如果不存在，则回答“NO"。

2.解析

可以通过回溯的方法，不断的为每一个节点着色，在前面n-1个节点都合法的着色之后，开始对第n个节点进行着色，这时候枚举可用的m个颜色，通过和第n个节点相邻的节点的颜色，来判断这个颜色是否合法，如果找到那么一种颜色使得第n个节点能够着色，那么说明m种颜色的方案是可行的。

例：

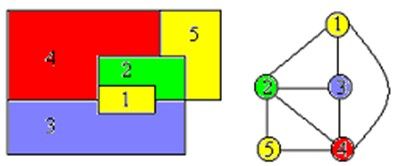
如图，5个顶点，4种颜色。
建立数组color存储各个顶点颜色，将数组各个元素初始化为0.
遍历图的邻接数组。

顶点一：
先将color[1]的值加1，即此时color[1]填入颜色1，再遍历与顶点一相接的顶点，判断颜色是否冲突，与顶点一相接的顶点此时color数组中的值全为0，则顶点一填入颜色1.
顶点二：
先将color[2]的值加1，即此时color[2]填入颜色1，再遍历与顶点二相接的顶点，判断颜色是否冲突，与顶点二相接的顶点中有顶点一的颜色是1，则将color[2]再加1，再次遍历与顶点二相接的顶点，判断颜色是否冲突，判断无冲突则顶点二填入颜色2.

顶点三：
先将color[3]的值加1，即此时color[3]填入颜色1，再遍历与顶点三相接的顶点，判断颜色是否冲突，与顶点三相接的顶点中有顶点一的颜色是1，则将color[3]再加1，再次遍历与顶点三相接的顶点，与顶点三相接的顶点中有顶点二的颜色是1，则将color[3]再加1，判断颜色是否冲突，判断无冲突则顶点三填入颜色3.

顶点四：
同顶点三一样，找到与相接顶点已填入的颜色不冲突的颜色，填入，此时顶点四填入颜色4.

顶点五：
同上，但由于顶点五与顶点一不相接，所以顶点五填入颜色1就不冲突，即顶点五填入颜色一.

此时第一个结果已经产生并保存在了color数组内，此时color数组为{1，2，3，4，1}，即对这副图填入4个颜色的第一种解。

此时开始尝试第二个解，此时遍历顶点用的的指针仍指在最后一个顶点上，则将这个顶点尝试不同的颜色，即产生结果color={1,2,3,4,3},此时，前4个顶点的颜色保持为1，2，3，4的情况下无法再产生新的解，开始回溯。
将此时的最后一个顶点的颜色重置为0，并将指针指向倒数第二个顶点即顶点四。
由于顶点四已经是最后一个可选择的颜色（颜色4），则将顶点四的颜色也重置为0，并将指针再向前退一个顶点，即指向顶点三。
将顶点三尝试填入下一个颜色，即将color[3]+=1,验证是否冲突，并再次按之前的方式对顶点四、顶点五填入合适的颜色。
以此方式，回溯整个数组，即可找到所有可能的解。

3.设计

void set_color(int n, int m, int**num)
{
    int i, k;
    for (i = 1; i <= n; i++)
        color[i] = 0;
    k = 1;
    while (k >= 1)
    {
        color[k] = color[k] + 1;
        while (color[k] <= m) {
            if (is_true(k, num)) {
                break;
            }
            else {
                color[k] = color[k] + 1;
            }
        }
        if (color[k] <= m && k == n)
        {
            for (i = 1; i <= n; i++)
                printf("%d", color[i]);
            printf("\n");
        }
        else if (color[k] <= m && k < n)
            k = k + 1;
        else
        {
            color[k] = 0;
            k = k - 1;
        }
    }
    if (color[1] == 0) {
        printf("NO");
    }
}

4.分析

时间复杂度：O(3^n)

5.源码

https://github.com/RussellWu728/Algorithm_Homework/blob/master/%E4%BD%9C%E4%B8%9A12%E2%80%94%E5%9B%BE%E7%9A%84m%E7%9D%80%E8%89%B2%E9%97%AE%E9%A2%98/%E5%9B%BE%E7%9A%84m%E7%9D%80%E8%89%B2%E9%97%AE%E9%A2%98.cpp