爬山算法与模拟退火算法
爬山算法,是一种局部贪心的最优算法. 该算法的主要思想是:每次拿相邻点与当前点进行比对,取两者中较优者,作为爬坡的下一步.
可分为:
- 首选爬山算法
依次寻找该点x的邻近点中首次出现的比点x值高的点,将该点作为爬山的点. 依次循环,直至该点的邻近点中不再有比其大的点. - 最陡爬山算法
最陡爬山算法是在首选爬山算法上的一种改良,它规定每次选取邻近点值最大的那个点作为爬山的点.
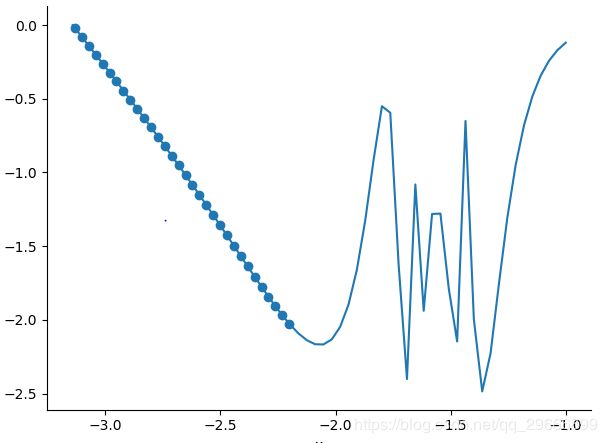
下面以函数:y = tan(sin(x)) - sin(tan(x))为例,求解局部最大值。
import random
import matplotlib.pyplot as plt
import numpy as np
class HillClimbing(object):
"""爬山算法"""
def __init__(self):
# x的定义域
self.x_range = np.array([-np.pi, -1])
# 画图所需的x, y数组
self.x = np.linspace(start=self.x_range[0], stop=self.x_range[1], num=60)
self.y = np.tan(np.sin(self.x)) - np.sin(np.tan(self.x))
# 随机产生的第一个值
self.first_value = random.uniform(-3, -1)
# figure 1
self.fig1 = plt.figure(num='fig1')
# 爬山路径
self.path = {self.first_value: self.evaluate(self.first_value)}
def evaluate(self, value):
"""计算结果"""
result = np.tan(np.sin(value)) - np.sin(np.tan(value))
return result
def creat_values(self, value, offset):
"""产生给定坐标的周围坐标"""
values = []
if -np.pi < value - offset < -1:
values.append(value - offset)
else:
values.append(None)
if -np.pi < value + offset < -1:
values.append(value + offset)
else:
values.append(None)
return values
def record_path(self, value, result):
"""记录路径,将每一步添加到路径列表中"""
self.path[value] = result
def draw_path(self):
"""画出路径"""
plt.figure(num='fig1')
keys = []
values = []
print(self.path)
for k, v in self.path.items():
keys.append(k)
values.append(v)
plt.scatter(x=keys, y=values)
def start_caculate(self):
# 当前x值等于第一个随机产生的x值
current_value = self.first_value
while True:
# 循环结束标志
flag = True
# 计算当前结果
current_result = self.evaluate(current_value)
# 将当前结果作为最好的结果
best_result = current_result
# 计算当前值的周围值
all_values = self.creat_values(current_value, 0.03)
# 对周围坐标计算其结果,并选出最优解
for each_value in all_values:
if each_value is not None:
result = self.evaluate(each_value)
if result > current_result:
# 记录路径
self.record_path(each_value, result)
# 更新当前值current_value,current_result, best_result
current_value = each_value
current_result = result
best_result = result
flag = False
if flag:
break
print('x:', current_value, 'best result:', best_result)
def show(self):
plt.figure(num='fig1')
plt.xlabel('x')
plt.ylabel('sin(x)')
axes = plt.gca()
axes.spines['right'].set_color('none')
axes.spines['top'].set_color('none')
plt.plot(self.x, self.y)
self.draw_path()
plt.show()
if __name__ == '__main__':
hill = HillClimbing()
hill.start_caculate()
hill.show()
x: -3.13 best result: -0.02
{-2.20: -2.02, -2.23: -1.96, -2.26: -1.90, -2.29: -1.84, -2.32: -1.77, -2.35: -1.70, -2.38: -1.63, -2.41: -1.56, -2.44: -1.49, -2.47: -1.42, -2.50: -1.35, -2.53: -1.28, -2.56: -1.22, -2.59: -1.15, -2.62: -1.08, -2.65: -1.01, -2.68: -0.95, -2.71: -0.88, -2.74: -0.82, -2.77: -0.75, -2.80: -0.69, -2.83: -0.63, -2.86: -0.56, -2.89: -0.50, -2.92: -0.44, -2.95: -0.38, -2.98: -0.32, -3.0: -0.26, -3.04: -0.20, -3.07: -0.14, -3.10: -0.08, -3.13: -0.02}
模拟退火算法
- 算法的提出
模拟退火算法最早的思想由Metropolis等(1953)提出,1983年Kirkpatrick等将其应用于组合优化。 - 算法的目的
解决NP复杂性问题;
克服优化过程陷入局部极小;
克服初值依赖性。
Boltzman概率分布告诉我们:
(1)在同一个温度,分子停留在能量小状态的概率大于停留在能量大状态的概率
(2)温度越高,不同能量状态对应的概率相差越小;温度足够高时,各状态对应概率基本相同。
(3)随着温度的下降,能量最低状态对应概率越来越大;温度趋于0时,其状态趋于1
Metropolis准则(1953)——以概率接受新状态
- 若在温度T,当前状态i → 新状态j
- 若Ej
- 否则,若概率 p=exp[-(Ej-Ei)/kT] 大于[0,1)区间的随机数,则仍接受状态 j 为当前状态;若不成立则保留状态 i 为当前状态。
其中k是波尔兹曼常数,值为k=1.3806488(13)×10−23,exp表示自然指数,且-(Ej-Ei)<0。因此[-(Ej-Ei)/kT]<0,所以p的取值范围是(0,1)。满足概率密度函数的定义。其实这条公式更直观意思就是:温度越高,出现一次能量差为p(dE)的降温的概率就越大;温度越低,则出现降温的概率就越小。
模拟退火算法的基本步骤:
1. 初始化,给定初始温度T, 最低温度Tmin, 初始状态x, 并计算出初始解result,同一温度下迭代次数N;
2. 产生新的状态x_new,并产生新解result_new
3. 计算函数差值Δf=f(x_new)−f(x)
4. 若Δf<=0,则接受此新解作为当前解
5. 若Δf>0,则以概率p=exp(−Δf/(kT))大于[0,1)区间的随机数接受此新解作为当前解
6. 对当前温度T迭代N次
7. 若满足终止条件则输出当前解为最优解,结束算法。否则降温,继续迭代。
以如下函数为例: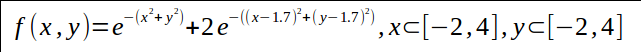
import random
import matplotlib.pyplot as plt
import numpy as np
from mpl_toolkits.mplot3d import Axes3D
class SimulatedAnnealing(object):
def __init__(self):
# x,y的定义域
self.x_range = np.array([-2, 4])
self.y_range = np.array([-2, 4])
# 画图所需的x, y数组
self.x = np.arange(-2, 4, 0.1)
self.y = np.arange(-2, 4, 0.1)
self.x, self.y = np.meshgrid(self.x, self.y)
self.z = self.evaluate(self.x, self.y)
# 随机登山点
len_x = len(self.x)
len_y = len(self.y)
self.current_x = self.x[0][random.randint(0, len_x - 1)]
self.current_y = self.y[random.randint(0, len_y - 1)][0]
self.current_result = self.evaluate(self.current_x, self.current_y)
print('first x:', self.current_x)
print('first y:', self.current_y)
# 初始化温度等值
self.T = 100
self.Tmin = 1e-10
self.N = 10
# figure 1
self.fig1 = plt.figure(num='fig1')
self.ax = Axes3D(self.fig1)
# 爬山路径
self.path = {(self.current_x, self.current_y): self.current_result}
def evaluate(self, x, y, x_move=1.7, y_move=1.7):
"""计算结果"""
def mul(x, y, alis=1):
return alis * np.exp(-(x * x + y * y))
return mul(x, y) + mul(x - x_move, y - y_move, 2)
def record_path(self, x, y, z):
"""记录路径,将每一步添加到路径列表中"""
self.path[(x, y)] = z
def draw_path(self):
"""画出路径"""
x = []
y = []
z = []
for k, v in self.path.items():
x_value, y_value = k
x.append(x_value)
y.append(y_value)
z.append(v)
self.ax.scatter(xs=x, ys=y, zs=z, color='r')
def start_caculate(self):
"""计算最值"""
while self.T > self.Tmin:
# 温度T下循环N次
for i in range(self.N):
# 随机产生一个新的邻近点
# 说明: 温度越高幅度邻近点跳跃的幅度越大
x_new = self.current_x + (random.random() * 2 - 1) * self.T
y_new = self.current_y + (random.random() * 2 - 1) * self.T
# 判断产生的点是否在定义域内
if 4 > x_new >= -2 and 4 > y_new >= -2:
# 新的结果
result_new = self.evaluate(x_new, y_new)
# 判断Δf的正负
if result_new - self.current_result > 0:
# 为正则接受为新解
self.record_path(x_new, y_new, result_new)
self.current_x = x_new
self.current_y = y_new
self.current_result = result_new
else:
# 为负则计算概率
p = 1.0 / (1.0 + np.exp(-(result_new - self.current_result) / self.T))
r = np.random.uniform(low=0, high=1)
# 判断是否可以接受为新解
if r < p:
self.record_path(x_new, y_new, result_new)
self.current_x = x_new
self.current_y = y_new
self.current_result = result_new
# 降温
self.T *= 0.95
print('max :', self.current_x, self.current_y, self.current_result)
def show(self):
self.ax.plot_surface(self.x, self.y, self.z, rstride=1, cstride=1, color='b')
self.ax.set_xlabel('x label', color='r')
self.ax.set_ylabel('y label', color='g')
self.ax.set_zlabel('z label', color='b')
self.draw_path()
plt.show()
if __name__ == '__main__':
sa = SimulatedAnnealing()
sa.start_caculate()
sa.show()
first x: 3.0000000000000044 first y: 3.7000000000000046
max :1.6973307001008588 1.6973306942718158 2.0031167460631685

参考:https://www.cnblogs.com/gongxijun/p/5873643.html
https://blog.csdn.net/zhouzi2018/article/details/82118673