树与二叉树
前言：数据结构到树开始就离开了我们熟悉的顺序结构，向着递归学习，所以这成了学习数据结构的门槛，很多同学跨这门槛过去的会扯着蛋，剩下的跨不下去。
希望我的对树与二叉树额理解与描述能帮助同学跨过这道门槛。（完全看完并理解，想相信这部分知识完全能掌握）
一.树
我们脑海中会浮现这样的图片
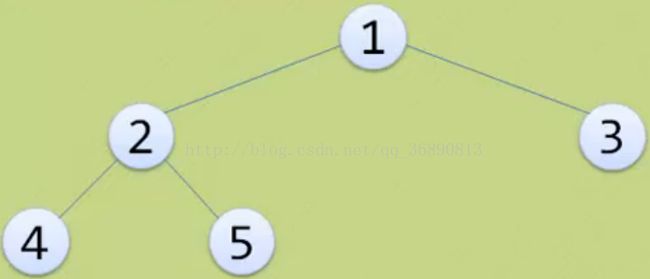
但数据结构的树比较难看了，是这样的
1.树的定义（我很讨厌定义，虽然说理论上是对的，但是看不懂，复杂，至少初学者看不明白）
树是n（n>=0）个结点的有限集。当n=0时成为空树，在任意一棵非空树中：
---有且仅有一个特定的称为根的结点：
---当n>1时，其余结点可分为m（m>0）个互不相同的有限集T1，T2、.........Tm，其中每一个集合本身又是一棵树，并且称为根的子树
2.结点分类
结点的度：拥有的子树数。
树的度：树各结点的度的最大值。
叶结点（终端结点）：度为0的结点。
分支结点（非终端结点）：度不为0的结点。
（如果结点外除外，那么分支结点也叫做内部结点）
3.结点间的关系
结点的孩子和双亲：结点的子树，相应的，该结点称为孩子的双亲。
结点的祖先：根到该结点所经过的所有结点（不包括该结点）。
然后堂兄弟，亲兄弟在此就不一一解释，看家谱能懂。
（枯燥的定义结束了，很开心）
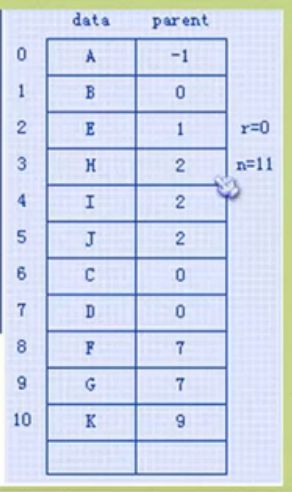
4.双亲表示法
该图截自小甲鱼视频
讲解：data存结点数据，parent存该结点的双亲结点的序号
下面是代码：
typedef struct {
char c;
int number;
}jiedian; （因为二维数组不能同时存字符和数字，所以用结构体模拟数组）
typedef struct{
jiedian[3];（创建了存放3个结点的类似于数组）
}shuzu;
以下是完整代码
#include
#define MANX 3
typedef struct {
char c;
int number;
}jiedian;
typedef struct{
jiedian zu[MANX];
}shuzu;
void shuru(shuzu *a){
char fuhao;
int i;
for(i = 0; i < 3; i++){
scanf("%c",&a->zu[i].c);
scanf("%d",&a->zu[i].number);
getchar();
}
}
void shuchu(shuzu a){
int i;
printf("结点 双亲结点序号\n");
for(i = 0; i < 3; i++){
printf("%c %d\n",a.zu[i].c,a.zu[i].number);
}
}
int main(){
shuzu a;
shuru(&a);
shuchu(a);
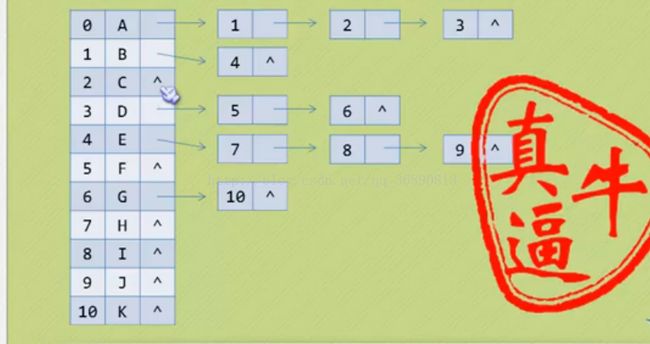
} 5.孩子表示法
（截图来自小甲鱼视频）
讲解：数组+链表的组合
以下是代码
#include
#include
#define MANX 3
typedef struct node{
int number;
struct node *next;
}*haizi;
typedef struct{
char c;
haizi many;
}shuju;
typedef struct{
shuju shuzu[MANX];
}zhengti;
void shuru(zhengti *a){
int i,j,k,shu;
char zifu;
haizi q,p;
for(i = 0; i < MANX; i++){
printf("该结点名字：");
scanf("%c",&a->shuzu[i].c);
printf("该结点孩子个数：");
scanf("%d",&shu);
a->shuzu[i].many = (haizi*)malloc(sizeof(haizi));
scanf("%d",&a->shuzu[i].many->number);
a->shuzu[i].many->next = NULL;
q = a->shuzu[i].many;
for(j = 1; j < shu; j++){
p = (haizi*)malloc(sizeof(haizi));
scanf("%d",&p->number);
q->next = p;
q = p;
q->next = NULL;
}
getchar();
}
}
void shuchu(zhengti a){
int i;
haizi q;
printf("结点 一系列孩子.......\n");
for(i = 0; i < MANX ; i++){
printf(" %c ",a.shuzu[i].c);
for(q = a.shuzu[i].many; q != NULL; q = q->next){
printf(" %d",q->number);
}
printf("\n");
}
}
int main(){
zhengti a;
shuru(&a);
shuchu(a);
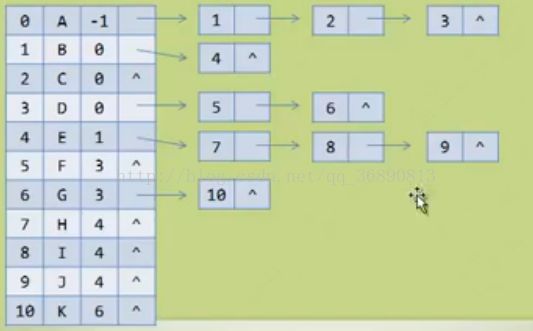
} 6.孩子双亲表示法（三种里最好的方法）
（截图来自小甲鱼视频）
讲解：链表+类似于数组，在孩子表示法中多加一个双亲数据域，总的来说是双亲表示法+孩子表示法，所以上面的双亲表示法和孩子表示法懂了，孩子双亲表示法不是问题（这也留给你们做测验，自己看能不能写出来）
二、二叉树
（截图来自小甲鱼视频）
1.二叉树的定义（枯燥的定义又来了555555）
二叉树是n（n>=0）个结点的有限集合，该集合或者为空集（空二叉树），或者由一个根结点或两棵互不相交的， 分别称为根结点的左子树和右子树的二叉树组成。
2.二叉树的特点
---每个结点最多有两棵子树，所以二叉树中不存在度大于2的结点。
---左子树和右子树是有顺序的，次序不能颠倒。
---即使树中某结点只有一棵子树，也要区分它是左子树还是右子树。
3.满二叉树
（截图来自小甲鱼视频）
定义：在一棵二叉树中，如果所有分支结点都存在左子树和右子树，并且所有叶子都在同一层，这样的二叉树称为满 二叉树。
特点：
---叶子只能出现在最下一层。
---非叶子结点的度一定是2。
---在同样深度的二叉树中，满二叉树的结点个数一定最多，同时叶子也是最多。
4.完全二叉树
（截图来自小甲鱼视频）
定义：对一棵具有n个结点的二叉树按层序编号，如果编号为i（1<=i<=n）的结点与同样深度的满二叉树中编号为i的 结点位置完全相同，则这课二叉树称为完全二叉树。
特点：
---叶子结点只能出现在最下两层。
---最下层的叶子一定集中在左部连续位置。
---倒数第二层，若有叶子结点，一定都在右部连续位置。
---如果结点度为一，则该结点只有左孩子。
---同样结点树的二叉树，完全二叉树的深度最小。
5.二叉树的性质
性质一：在二叉树的第i层上至多有2^(i-1)个结点（i>=1）。
性质二：深度为k的二叉树至多有2^k-1个结点（k>=1）。
性质三：对于任何一棵二叉树T，如果其终端结点数为n0,度为2的结点数为n2，则n0=n2+1。
性质四：具有n个结点的完全二叉树的深度为（log2n取下限）+1。
6.二叉树的遍历
定义：从根结点出发，按照某种次序依次访问二叉树中所有结点，使得每个结点被访问一次且仅被访问一次。
四种遍历方法：
---前序遍历（根结点，左子树，右子树）
---中序遍历（左子树，根结点，右子树）
---后序遍历（左子树，右子树，根结点）
---层序遍历（一层一层从左到右遍历）
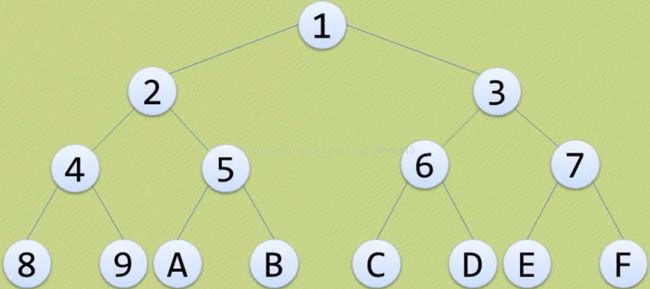
例子：
（截图来自小甲鱼视频）
前序遍历：A,B,D,H,I,E,J,C,F,K,G
中序遍历：H,D,I,B,E,J,A,F,K,C,G
后序遍历：H,I,D,J,E,B,K,F,G,C,A
层序遍历：A,B,C,D,E,F,G,H,I,J,K
7.二叉树的建立与遍历算法
（对指针变量的运用熟练）
#include
#include
typedef struct node{
char zifu;
struct node *lchild,*rchild;
}jiedian;
void createl(jiedian **t){ //前序遍历输入（可以更改）
char c;
scanf("%c",&c);
if(c == '#'){
(*t) = NULL;
}
else{
(*t) = (jiedian*)malloc(sizeof(jiedian));
(*t)->zifu = c;
createl(&(*t)->lchild);
createl(&(*t)->rchild);
}
}
void visit(jiedian **t){ //前序遍历输出（可以更改）
if((*t) == NULL){
return ;
}
else{
printf("%c",(*t)->zifu);
visit(&(*t)->lchild);
visit(&(*t)->rchild);
}
}
int main(){
jiedian * t;
createl(&t);
visit(&t);
} 到这里树和二叉树的基本东西已经讲完了，（终于轻松了，花了不少时间写这篇博客）不懂的加QQ1374487940询问，仅供参考。