使用python进行全面数据探索--House Prices: Advanced Regression Technique--kaggle入门(38)
一、翻译声明
本文为翻译Kaggle比赛House Prices: Advanced Regression Technique中Kernels的分享文章'Comprehensive data exploration with python'(国内访问速度较慢)。本文翻译进行了适当的删改,以突出重点。
二、正文翻译
本文根据Joseph F Hair 所著书籍《Multivariate Data Analysis》中 ‘Examining your data’这个章节所提供的方法对数据进行探索。主要包括:
1.单变量研究。分析因变量('SalePrice')。
2.多变量研究。分析自变量和自变量、自变量和因变量之间的关系。
3.数据清洗。清洗数据集、处理数据中的缺失数据、离群点等。
4.假设测试。对数据分布进行测试,以分析是否满足线性回归等技术的基础假设。
1、数据理解
首先引入分析数据所需要的Python库,读取训练数据和检查数据特征。
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import numpy as np
from scipy.stats import norm
from sklearn.preprocessing import StandardScaler
from scipy import stats
import warnings
warnings.filterwarnings('ignore')
%matplotlib inline
#读取训练csv文件
df_train = pd.read_csv('../input/train.csv')
#检查属性
df_train.columns
其次,为了理解我们的数据,我们需要查看每一个变量,试着理解他们的含义和它们与问题的关联。可以创建一个Excel表格来记录我们对数据的基础理解。
(1)变量 – 自变量名
(2)类型 – 自变量类型标识,包括但不限于数值型和类别型。
(3)类别 – 自变量类别标识,我们将变量的类别分为建筑类别、空间类别和位置类别。建筑类别变量指的是与房子的物理属性有关的变量(比如'OverallQual')。空间类别变量指的是与房子面积大小有关的变量(比如'TotalBsmtSF')。位置类别变量指的是与房子位置有关的变量(比如'Neighborhood')。
(4)期望 – 表示自变量对因变量'SalePrice'的影响程度。可以使用高、中和低来表示。
(5)结论 – 表示自变量的重要性,其功能与期望一样,但是期望记录的是主观感觉的高中低,而结论中自变量重要性需要一些数学方法进行验证。
(6)评述 – 任何对变量的补充说明。
为了填写这个列,我们应该阅读所有变量的描述并且问自己以下几个问题:
(1)当我们购买房子时,我们是否会考虑这个变量?(比如我们在购买房子时,是否会考虑'Masonry veneer type' ?)
(2)如果要考虑这个变量,那么它到底有多重要?(比如考虑房子外墙的材料是'Excellent'级别和'good'级别是否对购买产生影响?)
(3)这个变量是否已经被其他变量描述(比如如果'LandContour'描述了房子的平坦度,那我们真的需要知道'LandSlope'?)
我们通过询问自己的方式,就可以填充‘期望’这一列。然后,我们将画出每个自变量和因变量的散点图,以填充‘结论’这一列。通过这个步骤,总结出OverallQual,YearBuilt,TotalBsmtSF和GrLivArea四个最重要的变量。
2、单变量分析:因变量'SalePrice'可视化分析
#查看'SalePrice'的统计描述
df_train['SalePrice'].describe()
#直方图
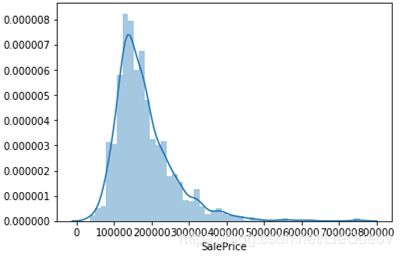
sns.distplot(df_train['SalePrice']);
通过观察直方图,'SalePrice'分布偏离正态分布,偏度为正。我们通过以下代码来精确计算'SalePrice'分布的偏度和峰度。
#偏度 和 峰度
print("Skewness: %f" % df_train['SalePrice'].skew())
print("Kurtosis: %f" % df_train['SalePrice'].kurt())
Tips: 偏度(Skewness)是指是统计数据分布偏斜方向和程度的度量,是统计数据分布非对称程度的数字特征。峰度(Kurtosis)是指表征概率密度分布曲线在平均值处峰值高低的特征数。直观看来,峰度反映了峰部的尖度。样本的峰度是和正态分布相比较而言统计量,如果峰度大于三,峰的形状比较尖,比正态分布峰要陡峭。反之亦然。在统计学中,峰度(Kurtosis)衡量实数随机变量概率分布的峰态。峰度高就意味着方差增大是由低频度的大于或小于平均值的极端差值引起的。(来自百度百科)
3、多变量分析:自变量与因变量'SalePrice'可视化分析
以数据理解中得出的结论,对OverallQual,YearBuilt,TotalBsmtSF、GrLivArea四个变量和SalePrice关系进行分析。
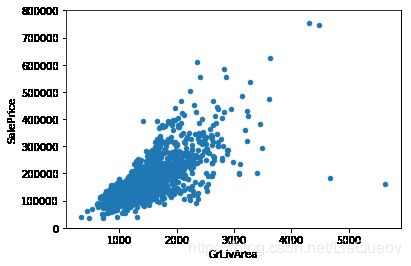
#画出 grlivarea和saleprice的散点图
var = 'GrLivArea'
data = pd.concat([df_train['SalePrice'], df_train[var]], axis=1)
data.plot.scatter(x=var, y='SalePrice', ylim=(0,800000));
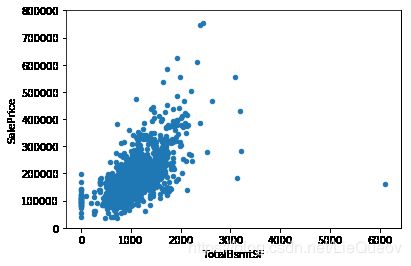
#画出 totalbsmtsf和saleprice的散点图
var = 'TotalBsmtSF'
data = pd.concat([df_train['SalePrice'], df_train[var]], axis=1)
data.plot.scatter(x=var, y='SalePrice', ylim=(0,800000));
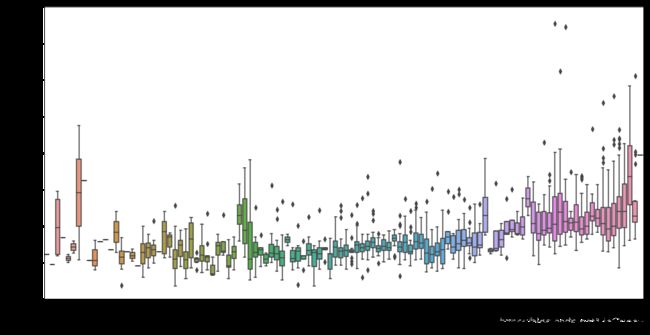
#画出 overallqual和saleprice的箱线图
var = 'OverallQual'
data = pd.concat([df_train['SalePrice'], df_train[var]], axis=1)
f, ax = plt.subplots(figsize=(8, 6))
fig = sns.boxplot(x=var, y="SalePrice", data=data)
fig.axis(ymin=0, ymax=800000);
var = 'YearBuilt'
data = pd.concat([df_train['SalePrice'], df_train[var]], axis=1)
f, ax = plt.subplots(figsize=(16, 8))
fig = sns.boxplot(x=var, y="SalePrice", data=data)
fig.axis(ymin=0, ymax=800000);
plt.xticks(rotation=90);
从以上的图形中可以看出,'GrLivArea'和'TotalBsmtSF'看起来与'SalePrice'是线性正相关的。并且'TotalBsmtSF'与'SalePrice'线性关系的斜率很高。'OverallQual'和'YearBuilt'看起来与'SalePrice'也是线性相关的。'OverallQual'与'SalePrice'的关系更加明显,品质越高,价格越高。
4、多变量分析:相关系数矩阵可视化分析
采用相关矩阵对变量关系进行分析,主要包括
(1)相关矩阵(热图样式)
(2)'SalePrice'相关矩阵(放大的热图样式)
(3)与'SalePrice'最相关自变量的散点图
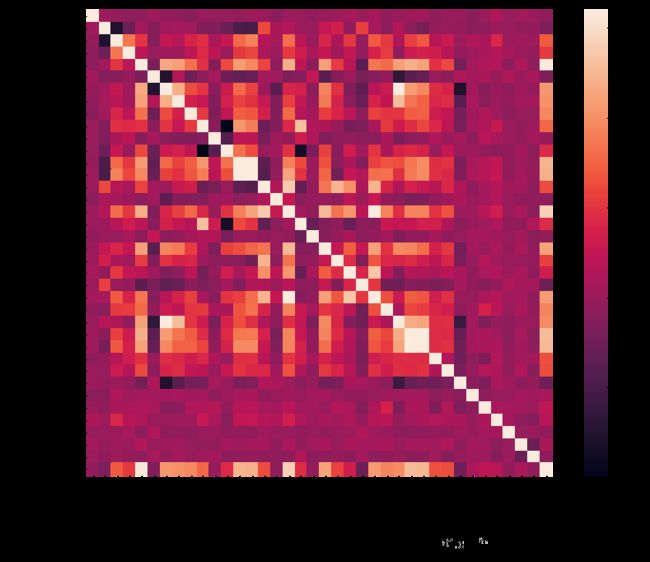
#相关矩阵
corrmat = df_train.corr()
f, ax = plt.subplots(figsize=(12, 9))
sns.heatmap(corrmat, vmax=.8, square=True);
如果两个自变量的相关性很强,它们交叉形成的方块颜色越偏向白色。可以认为两个相关性很强的特征提供的信息是相似的。如果使用相关性很高的特征用于模型学习可能会产生多重共线性问题。另外,我们发现与因变量'SalePrice'相关性很高的自变量为'GrLivArea', 'TotalBsmtSF' 和 'OverallQual'。这与我们之前的分析相同。
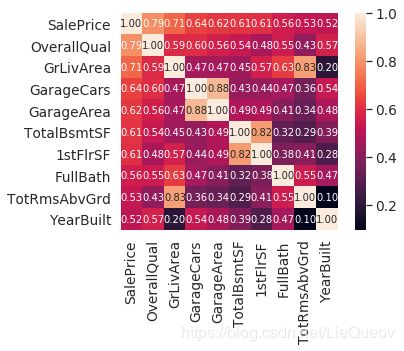
#saleprice 相关矩阵
k = 10 #number of variables for heatmap
cols = corrmat.nlargest(k, 'SalePrice')['SalePrice'].index
cm = np.corrcoef(df_train[cols].values.T)
sns.set(font_scale=1.25)
hm = sns.heatmap(cm, cbar=True, annot=True, square=True, fmt='.2f', annot_kws={'size': 10}, yticklabels=cols.values, xticklabels=cols.values)
plt.show()
相关系数矩阵热图分析:
(1)'OverallQual', 'GrLivArea' 和 'TotalBsmtSF' 与'SalePrice' 有很强的相关性。
(2)'GarageCars' 和 'GarageArea'的相关性很强。它们表达了相似的信息。因此,我们只需要保留其中一个自变量就行。我们保留'GarageCars',因为它与'SalePrice'的相关性更高。
(3)'TotalBsmtSF' and '1stFloor'相关性也很强,我们保留'TotalBsmtSF'。
(4)'TotRmsAbvGrd' and 'GrLivArea'相关性也很强。
(5)'YearBuilt'与'SalePrice'只有轻微的相关性,可能还需要进行时序分析。
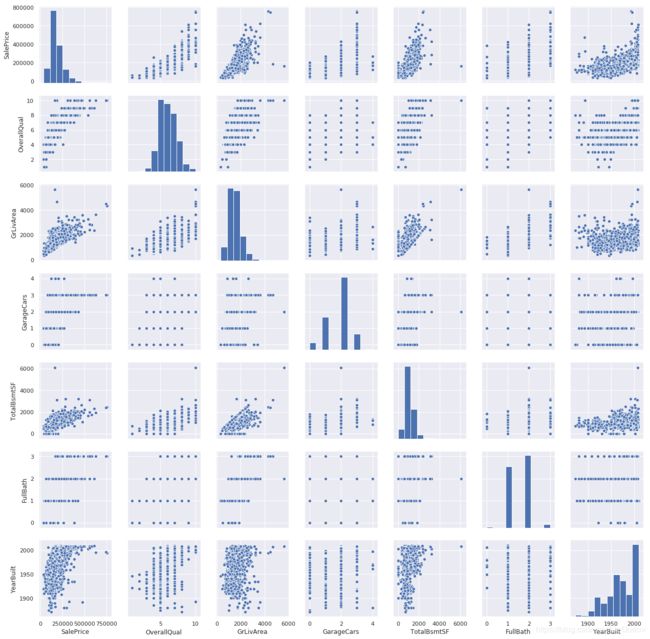
下面我们还可以画出与'SalePrice'相关性很高自变量,它们两两之间的散点图。
#scatterplot
sns.set()
cols = ['SalePrice', 'OverallQual', 'GrLivArea', 'GarageCars', 'TotalBsmtSF', 'FullBath', 'YearBuilt']
sns.pairplot(df_train[cols], size = 2.5)
plt.show();
图形分析:
(1)在'TotalBsmtSF' 和 'GrLiveArea'的图中,我们可以看出有些点可以连接成一条线。大部分点是在这条线下面的。表示地下室面积能够等于地上居住面积,但是并不希望地下室的面积超过地上居住面积。
(2)'SalePrice' 和 'YearBuilt'的图,在‘点云’的底部,'SalePrice'和'YearBuilt'似乎呈现了一种指数关系。在‘点云’的上限部分,我们也发现了这种趋势。
5、数据清洗:缺失数据分析
面对缺失数据,我们需要思考以下问题:
(1)缺失数据有多少?
(2)缺失数据是随机缺失还是存在一定的模式?
缺失数据表示样本容量的减少,我们需要确保处理缺失数据这个过程不带任何偏见。
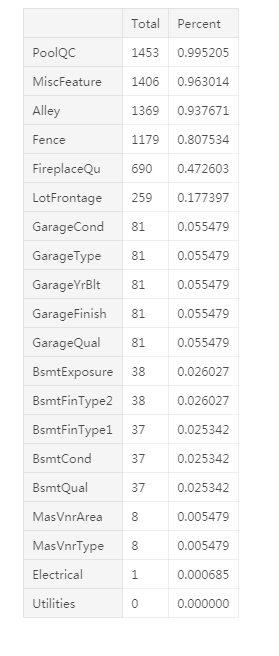
#显示缺失数据数量和比例
total = df_train.isnull().sum().sort_values(ascending=False)
percent = (df_train.isnull().sum()/df_train.isnull().count()).sort_values(ascending=False)
missing_data = pd.concat([total, percent], axis=1, keys=['Total', 'Percent'])
missing_data.head(20)
缺失数据处理:
(1)当缺失数据的比例超过15%时,我们删除对应的变量。这样的处理方式,使得我们不用去填充这些缺失值(比如'PoolQC', 'MiscFeature', 'Alley'等变量)。删除这些变量是否会缺失这些数据携带的信息?我认为不会。因为删除的变量中没有看起来特别重要的。因为当我们买房子的时候,一般不会考虑删除变量的因素。并且,再仔细分析一下,像'PoolQC', 'MiscFeature' 和 'FireplaceQu'这些变量,它们很有可能跟离群点有关。
(2)我们可以发现'GarageX'变量拥有相同的缺失数据,我打赌这些变量的缺失数据都来自相同的样本集合。因为关于车库最重要的信息可以通过'GarageCars'表达,我将会删除提到的'GarageX'变量。相同的逻辑也应用于'BsmtX'变量。
(3)再考虑'MasVnrArea' 和 'MasVnrType'属性,我认为这些变量不重要。并且它们和'YearBuilt' and 'OverallQual'有很强的相关性。因此,我删除了'MasVnrArea' and 'MasVnrType'两个属性。
总之,在处理缺失数据时,我们删除了除了'Electrical'变量外的其他和缺失数据有关的所有变量。'Electrical'变量只有1个样本缺失数据,我们直接删除了这个样本。
译者注:这种直接删除特征的方式,我觉得还是有值得商榷的空间,毕竟一个带有缺失值的属性,里面包含一些信息,但同时也包含有一定量的噪声。是否删除,还是需要实验确定。
#处理缺失数据
df_train = df_train.drop((missing_data[missing_data['Total'] > 1]).index,1)
df_train = df_train.drop(df_train.loc[df_train['Electrical'].isnull()].index)
df_train.isnull().sum().max() #检查是否还有缺失数据
6、数据清洗:离群点分析
离群点能够显著的影响我们的模型,并为一些特别的行为提供视角。我们通过'SalePrice'的标准差和一系列的散点图对离群点进行分析。我们需要设定一个阈值,超过或者低于这个阈值的样本就作为离群点。那么,首先我们需要标准化数据(即经过标准化后的数据均值为0,标准差为1)。
#标准化数据
saleprice_scaled = StandardScaler().fit_transform(df_train['SalePrice'][:,np.newaxis]);
low_range = saleprice_scaled[saleprice_scaled[:,0].argsort()][:10]
high_range= saleprice_scaled[saleprice_scaled[:,0].argsort()][-10:]
print('outer range (low) of the distribution:')
print(low_range)
print('\nouter range (high) of the distribution:')
print(high_range)
结果分析:
(1)较小的值离0不远
(2)较大的值的范围从0到7,这些较大的值值得注意。但是并没有删除相关值。
接着,可以分析重要自变量与因变量的散点图,比如自变量'GrLivArea'和‘SalePrice’的散点图(在第3部分图1呈现),会发现右下角两个点偏离主要点太远,而且他们表达的意思房屋面积很大,但是价格很便宜。显然,这两个点不太符合总体预测趋势。所以,我们删除了这两个点。
#删除离群点
df_train.sort_values(by = 'GrLivArea', ascending = False)[:2]
df_train = df_train.drop(df_train[df_train['Id'] == 1299].index)
df_train = df_train.drop(df_train[df_train['Id'] == 524].index)
当然,我们仅仅通过自变量'GrLivArea'和‘SalePrice’的散点图进行了举例,我们还可以按照相同的模式分析其他重要自变量和‘SalePrice’的散点图。
7、假设测试
以下4个假设应该被测试:
(1)正态性 – 正态性是指数据的分布应该看起来像正态分布。很多统计测试(比如t检验)都依靠这个假设,在这个部分,我们我们只测试了'SalePrice'的正态情况。但单变量的正态性并不能确保多变量的正态性,但对于多变量的正态化有帮助。如果数据具有正态性,我们也能避免很多问题(比如异方差性)。
(2)同方差性 – 总体回归函数中的随机误差项(干扰项)在解释变量条件下具有不变的方差(来自百度百科)。
(3)线性 – 通过散点图是检验线性的最普遍的方法,如果数据不是线性的,那么很有价值将数据进行变换。
(4)相关性错误 – 相关性错误,一个错误会关联另一个错误。这种情况经常在时序数据中发生,很多模式都是和时间相关的。如果你侦测到一些模式,可以试着增加一个相关的变量去解释这种影响。这是对相关性错误的最普遍的解决方案。
7.1 正态性测试
正态性测试可以采用以下两个方法
(1)柱状体 – 偏度和峰度
(2)正态概率图
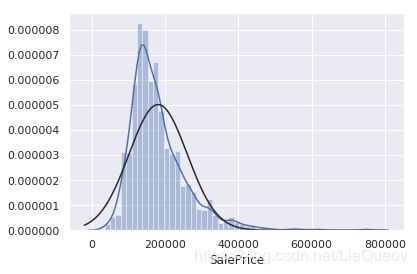
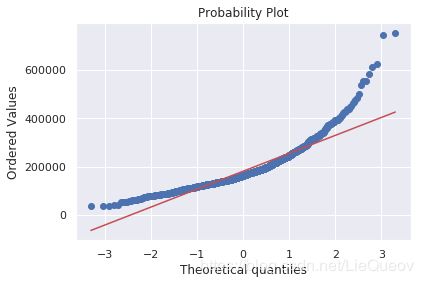
#柱状体和正态概率图
sns.distplot(df_train['SalePrice'], fit=norm);
fig = plt.figure()
res = stats.probplot(df_train['SalePrice'], plot=plt)
可以看出'SalePrice' 不是正态分布的。我们可以通过log变换,来解决这个问题。
#应用log变换
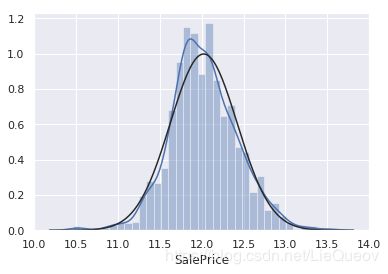
df_train['SalePrice'] = np.log(df_train['SalePrice'])
#经过log变换后的直方图和正态概率图
sns.distplot(df_train['SalePrice'], fit=norm);
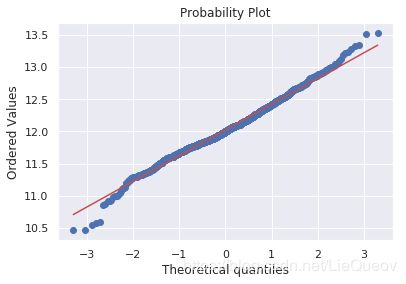
fig = plt.figure()
res = stats.probplot(df_train['SalePrice'], plot=plt)
同理,我们可以对其他变量的正态性进行分析,并进行log变换。
但是log变换也不是万能的,当样本值中有0时(比如没有地下室的房子),0值不能进行log变换。那么为了应用log变换,我们可以新设置了一个变量来表示是否有地下室(二进制变量)。然后,我们将会对所有非0的数据进行log变换。这种变换数据的方式,能够帮助我们不丢失是否有地下室的信息。但是,我也不能保证这种方法是完全正确。
#如果地下室面积大于0,则HasBsmt的取值为1,如果地下室的面积为0,则HasBsmt的取值为0.
df_train['HasBsmt'] = pd.Series(len(df_train['TotalBsmtSF']), index=df_train.index)
df_train['HasBsmt'] = 0
df_train.loc[df_train['TotalBsmtSF']>0,'HasBsmt'] = 1
#数据变换
df_train.loc[df_train['HasBsmt']==1,'TotalBsmtSF'] = np.log(df_train['TotalBsmtSF'])
#数据变换后的直方图和正态概率图
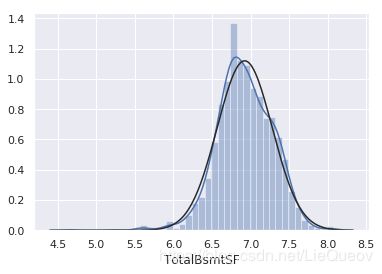
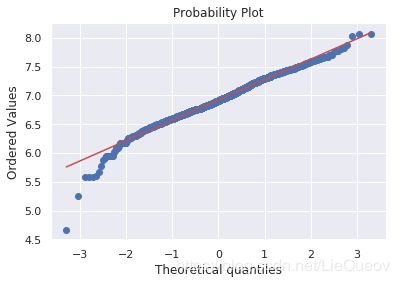
sns.distplot(df_train[df_train['TotalBsmtSF']>0]['TotalBsmtSF'], fit=norm);
fig = plt.figure()
res = stats.probplot(df_train[df_train['TotalBsmtSF']>0]['TotalBsmtSF'], plot=plt)
译者注:除了进行log变换外,Box-Cox变换更加实用。Box-Cox变换是Box和Cox在1964年提出的一种广义幂变换方法,是统计建模中常用的一种数据变换,用于连续的响应变量不满足正态分布的情况。Box-Cox变换之后,可以一定程度上减小不可观测的误差和预测变量的相关性。Box-Cox变换的主要特点是引入一个参数,通过数据本身估计该参数进而确定应采取的数据变换形式,Box-Cox变换可以明显地改善数据的正态性、对称性和方差相等性,对许多实际数据都是行之有效的。(来自百度百科)
7.2 同方差性分析(这个部分没太看懂,大家可以查阅原文)
测试同方差性最好的方式就是图形化两个变量。根据图中点偏离平均的情况(分散情况),进行分析。意思是通过log变换后,同方差性保证的很好。
总结
这篇文章中对变量相关矩阵可视化分析、散点图分析和正态变换值得学习。