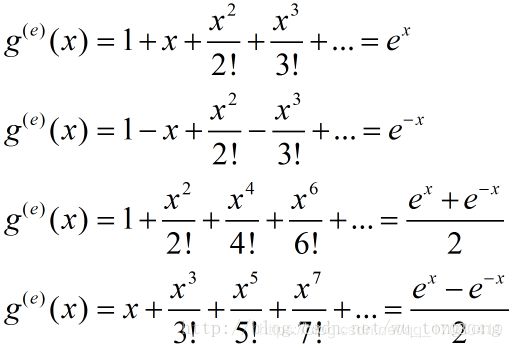生成函数知识总结
生成函数
- 基础知识
- OJ练习
- Fruit HDU - 2152(普通生成函数)
- 排列组合 HDU - 1521(指数生成函数)
- Ignatius and the Princess III HDU - 1028(普通生成函数)
- Holding Bin-Laden Captive! HDU - 1085(普通生成函数)
- 悼念512汶川大地震遇难同胞——来生一起走 HDU - 2189(普通生成函数)
- BZOJ3028: 食物(普通生成函数 + 推导 + 欧拉降幂)
- E. Counting Sequences II The Preliminary Contest for ICPC Asia Shanghai 2019 (指数生成函数 + 推导)
基础知识
1、普通生成函数: k k k 种元素的多重集合的 r r r 组合数(有限和无限多重集都可以)
- 数列:1,1, 1, 1, 1的生成函数,也可以表示一个因子的限制
g ( x ) = 1 + x + x 2 + ⋯ + x n + ⋯ = ∑ n = 0 ∞ x n = 1 1 − x g(x)=1+x+x^2+\dots+x^n+\dots=\sum_{n=0}^{\infty} x^n =\frac 1{1-x} g(x)=1+x+x2+⋯+xn+⋯=n=0∑∞xn=1−x1 - e 1 + e 2 + ⋯ + e k = n e_1+e_2+\dots+e_k=n e1+e2+⋯+ek=n 的正整数解为: C n + k − 1 n C_{n+k-1}^n Cn+k−1n。其生成函数如下
g ( x ) = ∑ n = 0 ∞ C n + k − 1 n x n = 1 ( 1 − x ) k g(x)=\sum_{n=0}^{\infty}C_{n+k-1}^n x^n=\frac {1}{(1-x)^k} g(x)=n=0∑∞Cn+k−1nxn=(1−x)k1
2、指数生成函数: k k k 种元素的多重集合的 r r r 排列数(有限和无限多重集都可以)
OJ练习
Fruit HDU - 2152(普通生成函数)
#include <bits/stdc++.h>
using namespace std;
int n,m;
int a[110],b[110],C1[110],C2[110];
int solve()
{
for(int i=0;i<=m;++i)
C1[i]=C2[i]=0;
for(int i=a[1];i<=b[1];++i)
C1[i]=1;
for(int i=2;i<=n;++i)
{
for(int j=0;j<=m;++j)
for(int k=a[i];k<=b[i];++k)
C2[j+k]+=C1[j];
for(int j=0;j<=m;++j)
C1[j]=C2[j],C2[j]=0;
}
return C1[m];
}
int main()
{
while(~scanf("%d%d",&n,&m))
{
for(int i=1;i<=n;++i)
scanf("%d%d",&a[i],&b[i]);
printf("%d\n",solve());
}
return 0;
}
排列组合 HDU - 1521(指数生成函数)

链接:http://acm.hdu.edu.cn/showproblem.php?pid=1521
#include <bits/stdc++.h>
using namespace std;
int n,m;
int a[110],b[110];
double fac[110];
double C1[110],C2[110];
void init()
{
fac[0]=fac[1]=1;
for(int i=2;i<=100;++i)
fac[i]=fac[i-1]*i;
}
double solve()
{
for(int i=0;i<=m;++i)
C1[i]=C2[i]=0;
for(int i=0;i<=a[1];++i)
C1[i]=1.0/fac[i];
for(int i=2;i<=n;++i)
{
for(int j=0;j<=m;++j)
{
for(int k=0;k<=a[i];++k)
{
C2[j+k]+=C1[j]*1.0/fac[k];
}
}
for(int j=0;j<=m;++j)
C1[j]=C2[j],C2[j]=0;
}
return C1[m]*fac[m];
}
int main()
{
init();
while(~scanf("%d%d",&n,&m))
{
for(int i=1;i<=n;++i)
scanf("%d",&a[i]);
printf("%.0lf\n",solve());
}
return 0;
}
Ignatius and the Princess III HDU - 1028(普通生成函数)
链接
题意:将整数n拆分成正整数相加的形式,问有几种组合
思路:每一个小于n的正整数都有可能组成。共有n个因子。可以得到生成函数
g ( x ) = ( 1 + x + x 2 + … ) ( 1 + x 2 + x 4 + … ) ( 1 + x 3 + x 6 + … ) … g(x)=(1+x+x^2+\dots)(1+x^2+x^4+\dots)(1+x^3+x^6+\dots)\dots g(x)=(1+x+x2+…)(1+x2+x4+…)(1+x3+x6+…)…
x n x^n xn的系数就是所求的组合方式
#include <iostream>
#include <algorithm>
#include <cstdio>
#define rep(i,a,b) for (int i=a; i<=b; ++i)
using namespace std;
const int maxn=130+5,INF=0x3f3f3f3f;
int N,C1[maxn],C2[maxn];
int solve(int n)
{
rep(i,0,n)
C1[i]=1,C2[i]=0;
for(int i=2;i<=n;++i)
{
for(int j=0;j<=n;++j)
{
for(int k=0;k+j<=n;k+=i)
{
C2[j+k]+=C1[j];
}
}
for(int j=0;j<=n;++j)
{
C1[j]=C2[j];
C2[j]=0;
}
}
return C1[n];
}
int main()
{
while(~scanf("%d",&N))
{
int ans=solve(N);
printf("%d\n",ans);
}
return 0;
}
Holding Bin-Laden Captive! HDU - 1085(普通生成函数)
链接
题意:由面值为1、2、5的硬币不能组成的最小面值是多少。
思路:可以得到生成函数
g ( x ) = ( 1 + x + x 2 + … ) ( 1 + x 2 + x 4 + … ) ( 1 + x 5 + x 10 ) g(x)=(1+x+x^2+\dots)(1+x^2+x^4+\dots)(1+x^5+x^{10}) g(x)=(1+x+x2+…)(1+x2+x4+…)(1+x5+x10)
从小到大遍历系数,为0的那一项就是不能组成的
#include <iostream>
#include <algorithm>
#include <cstdio>
#include <queue>
#include <vector>
#include <set>
#include <map>
#include <cstring>
#include <string>
#include <cmath>
#define rep(i,a,b) for (int i=a; i<=b; ++i)
#define per(i,b,a) for (int i=b; i>=a; --i)
#define mes(a,b) memset(a,b,sizeof(a))
#define mp make_pair
#define ll long long
#define pb push_back
#define pii pair<int,int>
#define pll pair<ll,ll>
#define ls (rt<<1)
#define rs ((rt<<1)|1)
#define isZero(d) (abs(d) < 1e-8)
using namespace std;
const int maxn=8000+5,INF=0x3f3f3f3f;
const int mod=1e9+7;
int C1[maxn],C2[maxn];
int main()
{
int n1,n2,n3;
while(scanf("%d%d%d",&n1,&n2,&n3)&&(n1||n2||n3))
{
rep(i,0,n1+2*n2+5*n3)
C1[i]=1,C2[i]=0;
for(int i=0;i<=n1;++i)
{
for(int j=0;j+i<=n1+2*n2;j+=2)
{
C2[j+i]+=C1[i];
}
}
for(int i=0;i<=n1+2*n2;++i)
C1[i]=C2[i],C2[i]=0;
for(int i=0;i<=n1+2*n2;++i)
{
for(int j=0;j+i<=n1+2*n2+5*n3;j+=5)
{
C2[j+i]+=C1[i];
}
}
for(int i=0;i<=n1+2*n2+5*n3;++i)
C1[i]=C2[i],C2[i]=0;
int i=0;
while(C1[i]!=0&&i<=n1+2*n2+5*n3)
i++;
printf("%d\n",i);
}
return 0;
}
悼念512汶川大地震遇难同胞——来生一起走 HDU - 2189(普通生成函数)
链接
题意:把n个人分成几个小组。每个小组的人数必须是素数
思路:用素数组成n,但是不知道用具体多少个素数。每一个小于等于n的素数都是一个因子。
可以得到生成函数:
g ( x ) = ( 1 + x 2 + x 4 + x 6 + … ) ( 1 + x 3 + x 6 + … ) ( 1 + x 5 + x 10 + … ) g(x)=(1+x^2+x^4+x^6+\dots)(1+x^3+x^{6}+\dots)(1+x^5+x^{10}+\dots) g(x)=(1+x2+x4+x6+…)(1+x3+x6+…)(1+x5+x10+…)
x n x^n xn的系数就是这个组合数的答案
#include <iostream>
#include <algorithm>
#include <cstdio>
#include <queue>
#include <vector>
#include <set>
#include <map>
#include <cstring>
#include <string>
#include <cmath>
#define rep(i,a,b) for (int i=a; i<=b; ++i)
#define per(i,b,a) for (int i=b; i>=a; --i)
#define mes(a,b) memset(a,b,sizeof(a))
#define mp make_pair
#define ll long long
#define pb push_back
#define pii pair<int,int>
#define pll pair<ll,ll>
#define ls (rt<<1)
#define rs ((rt<<1)|1)
#define isZero(d) (abs(d) < 1e-8)
using namespace std;
const int maxn=150+5,INF=0x3f3f3f3f;
int T,n;
int C1[maxn],C2[maxn];
const int N=300;
int visit[N],prime[N],cnt;
void Prime()
{
memset(visit,0,sizeof(visit));
memset(prime,0,sizeof(prime));
cnt=0;
for(int i=2;i<N;++i)
{
if(!visit[i])
prime[++cnt]=i;
for(int j=1;j<=cnt&&i*prime[j]<N;++j)
{
visit[i*prime[j]]=1;
if(i%prime[j]==0)
break;
}
}
}
int solve(int n)
{
mes(C1,0),mes(C2,0);
for(int i=0;i<=n;i+=2)
C1[i]=1;
for(int i=2;i<=cnt;++i)
{
for(int j=0;j<=n;++j)
{
for(int k=0;k+j<=n;k+=prime[i])
{
C2[k+j]+=C1[j];
}
}
for(int j=0;j<=n;++j)
C1[j]=C2[j],C2[j]=0;
}
return C1[n];
}
int main()
{
Prime();
scanf("%d",&T);
while(T--)
{
scanf("%d",&n);
int ans=solve(n);
printf("%d\n",ans);
}
return 0;
}
BZOJ3028: 食物(普通生成函数 + 推导 + 欧拉降幂)
Description
明明这次又要出去旅游了,和上次不同的是,他这次要去宇宙探险!
我们暂且不讨论他有多么NC,他又幻想了他应该带一些什么东西。理所当然的,你当然要帮他计算携带N件物品的方案数。
他这次又准备带一些受欢迎的食物,如:蜜桃多啦,鸡块啦,承德汉堡等等
当然,他又有一些稀奇古怪的限制:
每种食物的限制如下:
(1)承德汉堡:偶数个
(2)可乐:0个或1个
(3)鸡腿:0个,1个或2个
(4)蜜桃多:奇数个
(5)鸡块:4的倍数个
(6)包子:0个,1个,2个或3个
(7)土豆片炒肉:不超过一个。
(8)面包:3的倍数个
注意,这里我们懒得考虑明明对于带的食物该怎么搭配着吃,也认为每种食物都是以‘个’为单位(反正是幻想嘛),只要总数加起来是N就算一种方案。因此,对于给出的N,你需要计算出方案数,并对10007取模
思路:很明显示生成函数的题,并且考虑的是组合数
可以得到生成函数:
g ( x ) = ( 1 + x 2 + … ) ( 1 + x ) ( 1 + x + x 2 ) ( x + x 3 + … ) ( 1 + x 4 + x 8 + … ) ( 1 + x + x 2 + x 3 ) ( 1 + x ) ( 1 + x 3 + x 6 + … ) g(x)=(1+x^2+\dots )(1+x)(1+x+x^2)(x+x^3+\dots)(1+x^4+x^8+\dots)(1+x+x^2+x^3)(1+x)(1+x^3+x^6+\dots) g(x)=(1+x2+…)(1+x)(1+x+x2)(x+x3+…)(1+x4+x8+…)(1+x+x2+x3)(1+x)(1+x3+x6+…)
g ( x ) = 1 1 − x 2 ( 1 + x ) 1 − x 3 1 − x x 1 1 − x 2 1 1 − x 4 ( 1 − x 4 1 − x ) 1 1 − x 3 g(x)=\frac 1{1-x^2}(1+x)\frac {1-x^3}{1-x}x\frac 1{1-x^2}{\frac {1}{1-x^4}}(\frac {1-x^4}{1-x})\frac 1{1-x^3} g(x)=1−x21(1+x)1−x1−x3x1−x211−x41(1−x1−x4)1−x31
g ( x ) = x ( 1 − x ) 4 = ∑ n = 0 ∞ C n + 4 − 1 3 x n + 1 = ∑ n = 0 ∞ C n + 2 3 x n g(x)=\frac x{(1-x)^4}=\sum_{n=0}^{\infty}C_{n+4-1}^3x^{n+1}=\sum_{n=0}^{\infty}C_{n+2}^3x^n g(x)=(1−x)4x=n=0∑∞Cn+4−13xn+1=n=0∑∞Cn+23xn
因此,答案就是 a n = C n + 2 3 a_n=C_{n+2}^3 an=Cn+23

#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int Maxn=510;
const int mod=10007;
char s[Maxn];
ll QuickPower(ll base,ll n)
{
ll ret=1;
while(n)
{
if(n&1)
ret=(ret*base)%mod;
n>>=1;
base=(base*base)%mod;
}
return ret;
}
int main()
{
scanf("%s",s+1);
int n=0,len=strlen(s+1);
for(int i=1;i<=len;i++)
n=(n*10%mod+s[i]-'0')%mod;
ll ans=n*(n+1)%mod*(n+2)%mod*QuickPower(6,mod-2)%mod;
printf("%lld\n",ans);
}
E. Counting Sequences II The Preliminary Contest for ICPC Asia Shanghai 2019 (指数生成函数 + 推导)
链接
题意:给定n个位置,对于每一个数 a i a_i ai,都满足 1 ≤ a i ≤ m 1\le a_i \le m 1≤ai≤m,并且如果 a i a_i ai是偶数的话, a i a_i ai出现的次数是偶数次,求排列的个数
思路:求的是排列,所以是指数型生成函数。在[1,m]的范围内,相当于有m个因子,每个因子分别代表对 1 、 2 、 3 、 4 、 … 、 m 1、2、3、4、\dots、m 1、2、3、4、…、m各自的限制。其中偶数有 f l o o r ( m 2 ) floor(\frac m2) floor(2m)个,奇数有 m − f l o o r ( m 2 ) m-floor(\frac m2) m−floor(2m),设 t = f l o o r ( m 2 ) t=floor(\frac m2) t=floor(2m),可以得到指数型生成函数
g ( x ) = ( 1 + x + x 2 2 ! + x 3 3 ! + … ) m − t ( 1 + x 2 2 ! + x 4 4 ! + … ) t g(x)=(1+x+\frac {x^2}{2!}+\frac {x^3}{3!}+\dots)^{m-t}(1+\frac {x^2}{2!}+\frac {x^4}{4!}+\dots)^{t} g(x)=(1+x+2!x2+3!x3+…)m−t(1+2!x2+4!x4+…)t
化简可得:
g ( x ) = e x ( m − t ) ( e x + e − x 2 ) t = e x ( m − t ) ∑ i = 0 t C t i e x ( t − i ) e − x i 2 t g(x)=e^{x(m-t)}(\frac {e^x+e^{-x}}2)^t=\frac{e^{x(m-t)}\sum_{i=0}^tC_t^ie^{x(t-i)}e^{-xi}}{2^t} g(x)=ex(m−t)(2ex+e−x)t=2tex(m−t)∑i=0tCtiex(t−i)e−xi
g ( x ) = ∑ i = 0 t C t i e ( m − 2 i ) x 2 t = ∑ n = 0 ∑ i = 0 t C t i ( m − 2 i ) n 2 t x n n ! g(x)=\frac {\sum_{i=0}^tC_t^ie^{(m-2i)x}}{2^t}=\sum_{n=0}\frac{\sum_{i=0}^tC_t^i{(m-2i)^n}}{2^t}\frac {x^n}{n!} g(x)=2t∑i=0tCtie(m−2i)x=n=0∑2t∑i=0tCti(m−2i)nn!xn
因此可以得到 a n = ∑ i = 0 t C t i ( m − 2 i ) n 2 t a_n=\frac{\sum_{i=0}^tC_t^i{(m-2i)^n}}{2^t} an=2t∑i=0tCti(m−2i)n, a n a_n an就是答案
#include <iostream>
#include <algorithm>
#include <cstdio>
#define rep(i,a,b) for (int i=a; i<=b; ++i)
#define ll long long
using namespace std;
const int maxn=1e5+5,INF=0x3f3f3f3f;
const int mod=1e9+7;
int T;
ll n,m;
ll QuickPower(ll base,ll n,ll mod)
{
ll ret=1;
while(n)
{
if(n&1)
ret=(ret*base)%mod;
n>>=1;
base=(base*base)%mod;
}
return ret;
}
const int N=2e5+10;
ll fac[N+10],finv[N+10];
void init()
{
fac[0]=fac[1]=1;
for(int i=2;i<=N;++i)
fac[i]=fac[i-1]*i%mod;
finv[N]=QuickPower(fac[N],mod-2,mod);
for(int i=N-1;i>=0;--i)
finv[i]=finv[i+1]*(i+1)%mod;
}
int main()
{
init();
scanf("%d",&T);
while(T--)
{
scanf("%lld%lld",&n,&m);
ll ans=0;
int t=m/2;
for(int i=0;i<=t;++i)
{
ans=(ans+fac[t]*finv[i]%mod*finv[t-i]%mod*QuickPower(m-2*i,n,mod)%mod)%mod;
}
ll x=QuickPower(2,t,mod);
ans=ans*QuickPower(x,mod-2,mod)%mod;
printf("%lld\n",ans);
}
return 0;
}