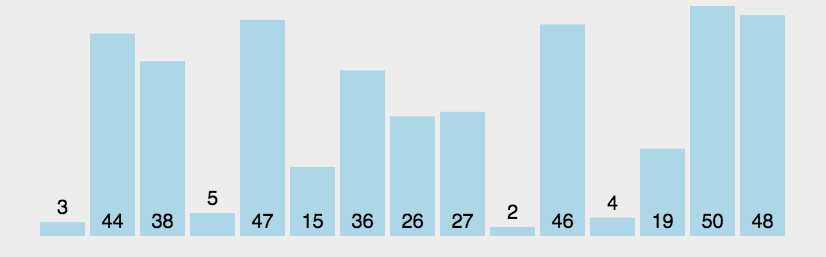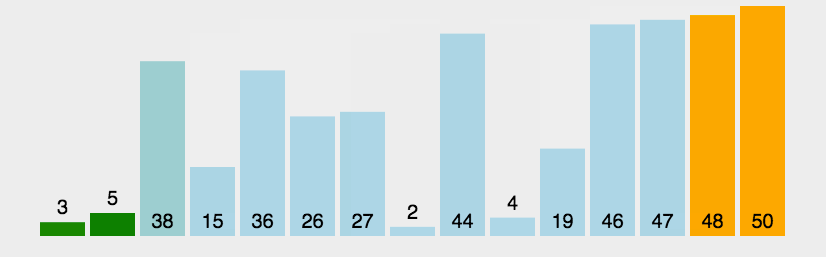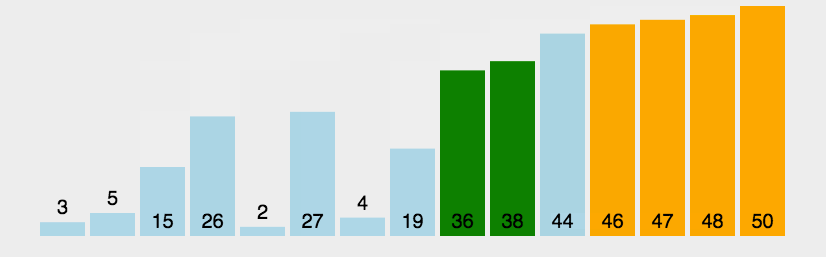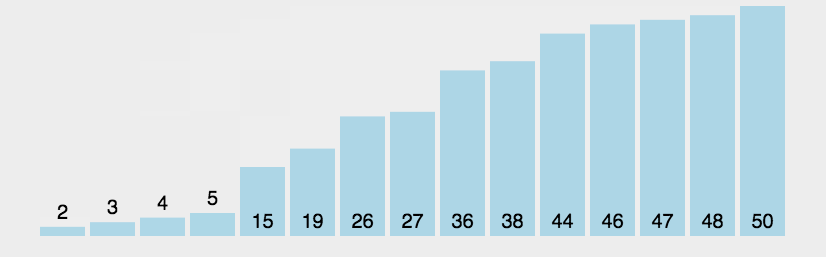七大经典排序算法

七大经典排序算法

1.冒泡算法

1.基本介绍
冒泡排序（Bubble Sorting）的基本思想是：通过对待排序序列从前向后（从下标较小的元素开始），以此比较相邻元素的值，若发现逆序则交换，数值较大的元素逐渐从前移后部，就像水底下的气泡一样逐渐向上冒。
因为排序的过程中，各元素不断接近自己的位置，如果一趟比较下来没有进行过交换，就说明序列有序，因此要在排序过程中设置一个标志flag判断元素是否进行过交换。从而减少不必要的比较。

2.动态效果图

冒泡排序（BubbleSort）动图展示

3.相关详细文章
【Java数据结构与算法】冒泡排序

4.代码实现

public static void bubbleSort(int[] arr) {
        int temp = 0;
        boolean flag = false;
        for (int i = 0;i < arr.length - 1;i ++) {
            for (int j = 0;j < arr.length - 1 - i;j ++) {
                if (arr[j] > arr[j + 1]) {
                    flag = true;
                    temp = arr[j];
                    arr[j] = arr[j + 1];
                    arr[j + 1] = temp;
                }
            }
            if (flag == false) {
                break;
            } else {
                flag = false;
            }
        }
    }

2.选择排序

1.基本介绍
选择式排序也属于内部排序法，是从欲排序的数据中，按指定的规则选出某一元素，再依规定交换位置后达到排序的目的。
选择排序思想：
选择排序（select sorting）也是一种简单的排序方法，它的基本思想是：第一次从arr[0]~arr[n-1]中选取最小值，与arr[0]交换，第二次从arr[1]~arr[n-1]中选取最小值，与arr[1]交换，第三次从arr[2]~arr[n-1]中选取最小值，与arr[2]交换，…，第i次从arr[i-1]~arr[n-1]中选取最小值，与arr[i-1]交换，…，第n-1
次从arr[n-2]~arr[n-1]中选取最小值，与arr[n-2]交换，总共通过n-1次，得到一个按排序码从小到大排序的有序序列。

2.动态效果图

选择排序（SelectSort）动图展示

3.相关详细文章
【Java数据结构与算法】选择排序

4.代码实现

public static void selectSort(int[] arr) {
        for (int i = 0; i < arr.length - 1; i++) {
            int minIndex = i;
            int min = arr[i];
            for (int j = i + 1; j < arr.length; j++) {
                if (min > arr[j]) {
                    min = arr[j];
                    minIndex = j;
                }
            }
            if (minIndex != i) {
                arr[minIndex] = arr[i];
                arr[i] = min;
            }
        }
    }

3.插入排序

1.基本介绍
插入式排序属于内部排序法，式对于要排序的元素以插入的方式寻找该元素的适当位置，以达到排序的目的。
插入排序思想：
插入排序（Insertion Sorting）的基本思想是：把n个待排序的元素看成为一个有序表和一个无序表，开始有序表中只包含一个元素。无序表当主包含n-1个元素。排序过程中每次从无序表中取出第一个元素，把它的排序码以此与有序表元素的排序码进行比较，将他插入到有序表中的适当位置，使之称为新的有序表。

2.动态效果图

插入排序（InsertSort）动图展示

3.相关详细文章
【Java数据结构与算法】插入排序

4.代码实现

public static void insertSort(int[] arr) {
        for (int i = 1;i < arr.length;i ++) {
            int inertVal = arr[i];
            int insertIndex = i - 1;
            while (insertIndex >= 0 && inertVal < arr[insertIndex]) {
                arr[insertIndex + 1] = arr[insertIndex];
                insertIndex--;
            }
            if (insertIndex + 1 != i) {
                arr[insertIndex + 1] = inertVal;
            }
        }
    }

4.希尔排序

1.基本介绍
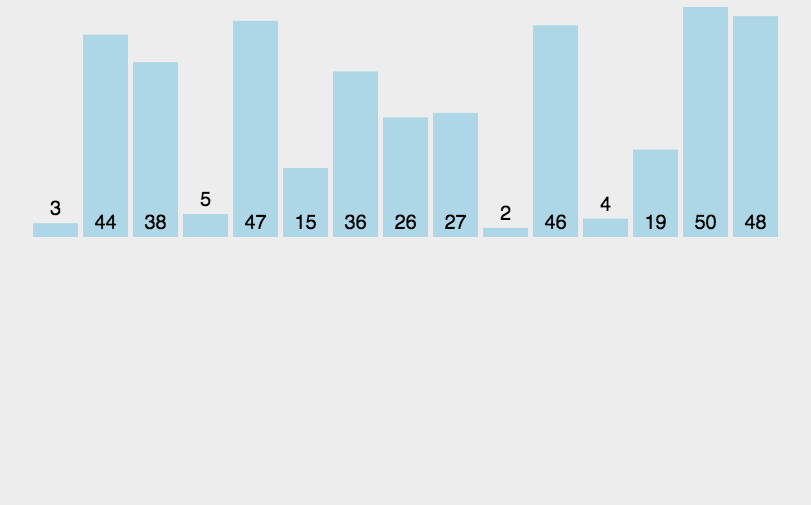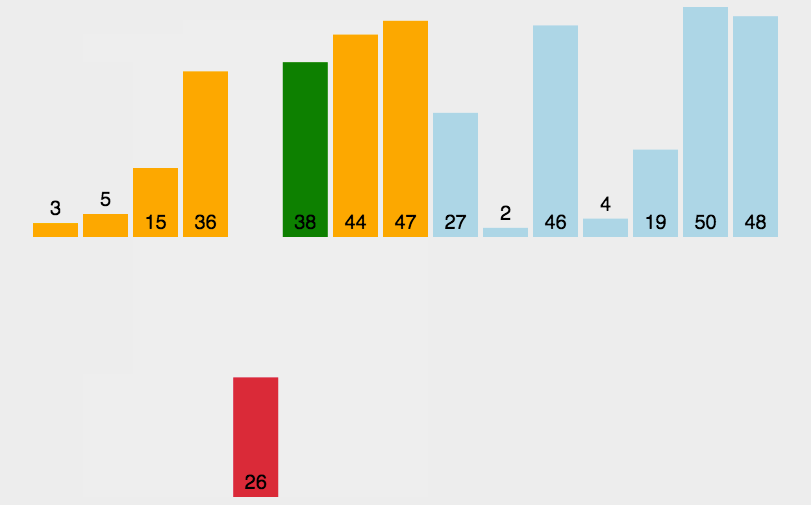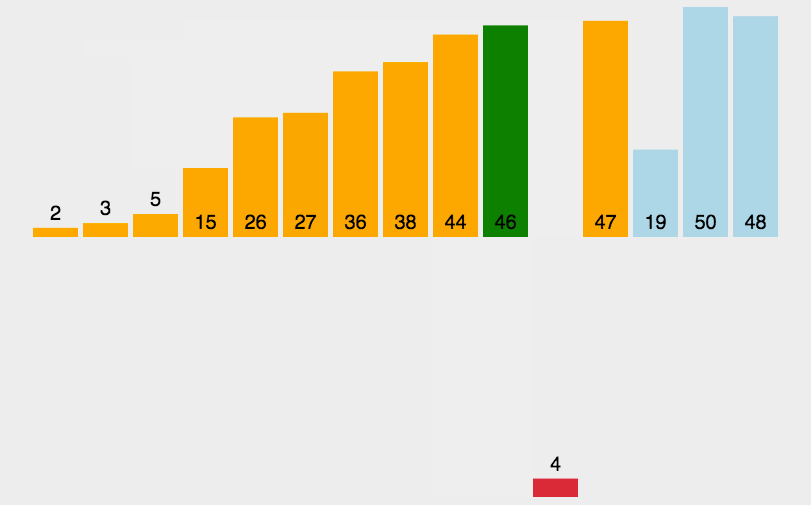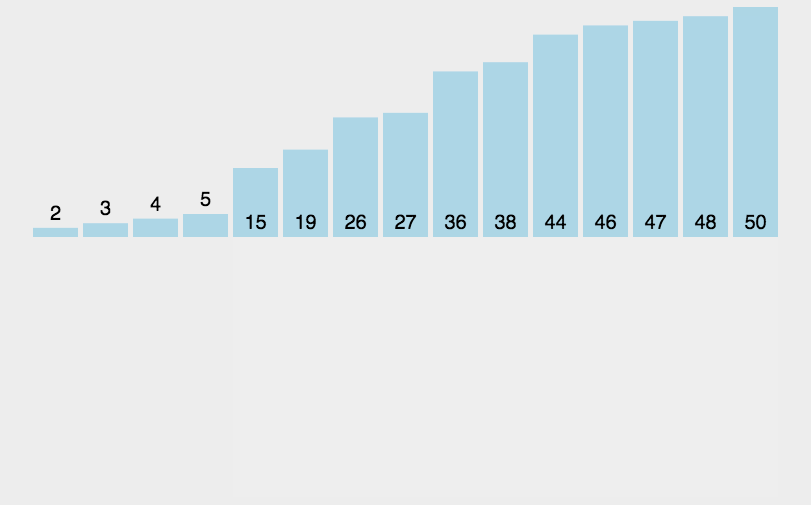
希尔排序是希尔（DonaldShell）于1959年提出的一种排序算法。希尔排序也是一种插入排序，它是简单插入排序经过改进之后的一个更高效的版本，也称为缩小增量排序。

插入排序文章：插入排序
希尔排序是把记录按下标的一定增量分组，对每组使用直接插入排序算法排序；随着增量逐渐减少，每组包含的关键词越来越多，当增量减至1时，整个文件恰被分成一组，算法便停止。

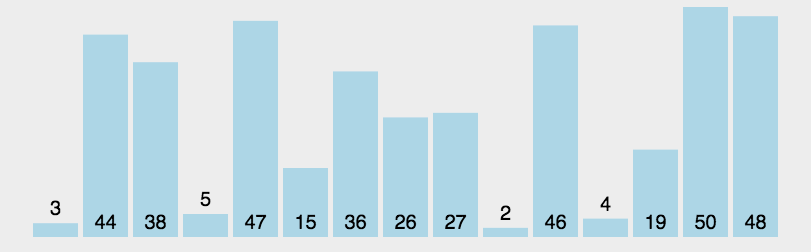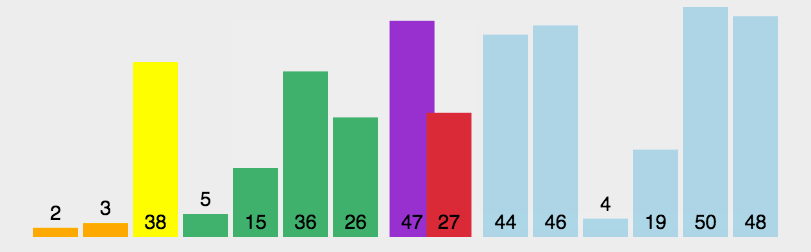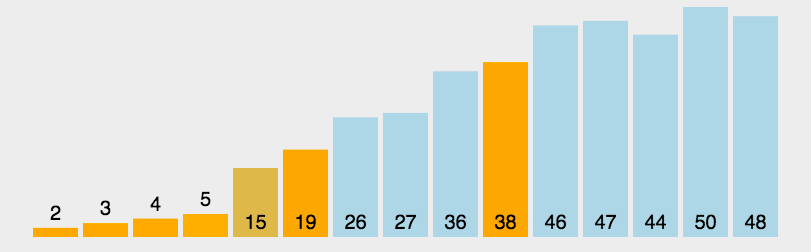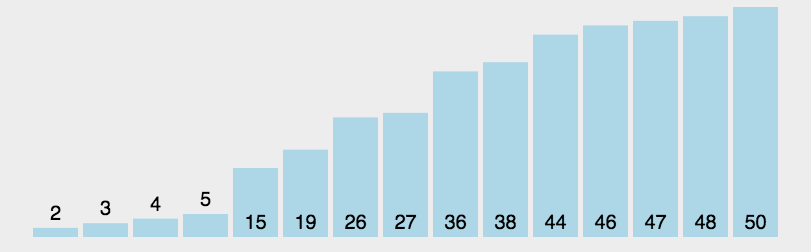
2.动态效果图

希尔排序（ShellSort）动图展示

3.相关详细文章
【Java数据结构与算法】希尔排序

4.代码实现

public static void shellSort(int[] arr) {
        int temp = 0;
        for (int gap = arr.length / 2;gap > 0;gap /= 2) {
            for (int i = gap;i < arr.length;i ++) {
                for (int j = i - gap;j >= 0;j -= gap) {
                    if (arr[j] > arr[j + gap]) {
                        temp = arr[j];
                        arr[j] = arr[j + gap];
                        arr[j + gap] = temp;
                    }
                }
            }
        }
    }

5.快速排序

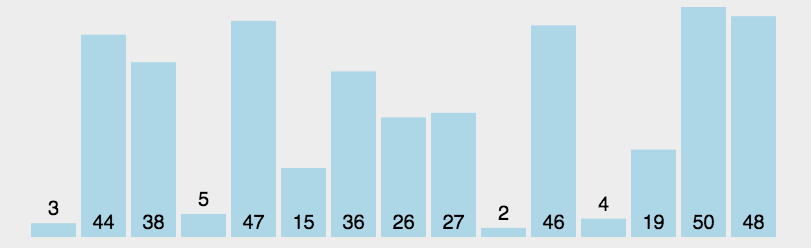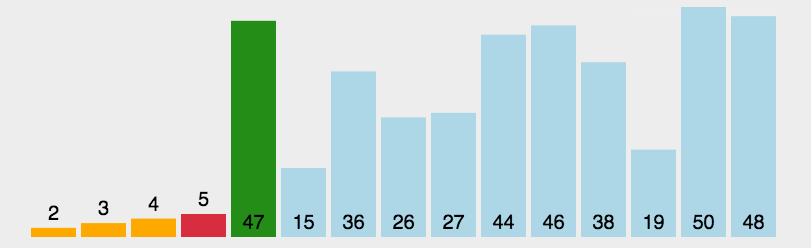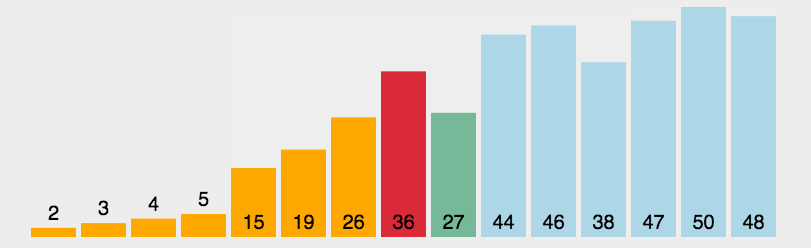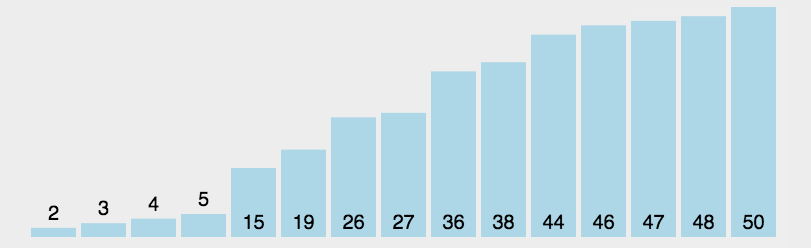
1.基本介绍

快速排序（Quick sort）是对冒泡排序的一种改进。基本思想是：通过一趟排序将要排序的数据分割成独立的两部分，其中一部分的所有数据都比另外一部分的所有数据都要小，然后再按照此方法对这两部分数据分班进行快速排序。整个排序过程可以递归进行，以此达到整个数据变成有序序列。

2.动态效果图

快速排序（QuickSort）动图展示

3.相关详细文章
【Java数据结构与算法】快速排序

4.代码实现

public static void quickSort(int[] arr,int left,int right) {
        int l = left;
        int r = right;
        //pivot中轴
        int pivot = arr[(left + right) / 2];
        int temp = 0;
        while (l < r) {
            while (arr[l] < pivot) {
                l += 1;
            }
            while (arr[r] > pivot) {
                r -= 1;
            }
            if (l >= r) {
                break;
            }
            temp = arr[l];
            arr[l] = arr[r];
            arr[r] = temp;
            if (arr[l] == pivot) {
                r -= 1;
            }
            if (arr[r] == pivot) {
                l += 1;
            }
        }
        if (l == r) {
            l += 1;
            r -= 1;
        }
        if (left < r) {
            quickSort(arr,left,r);
        }
        if (right > l) {
            quickSort(arr,l,right);
        }
    }

6.归并排序

1.基本介绍
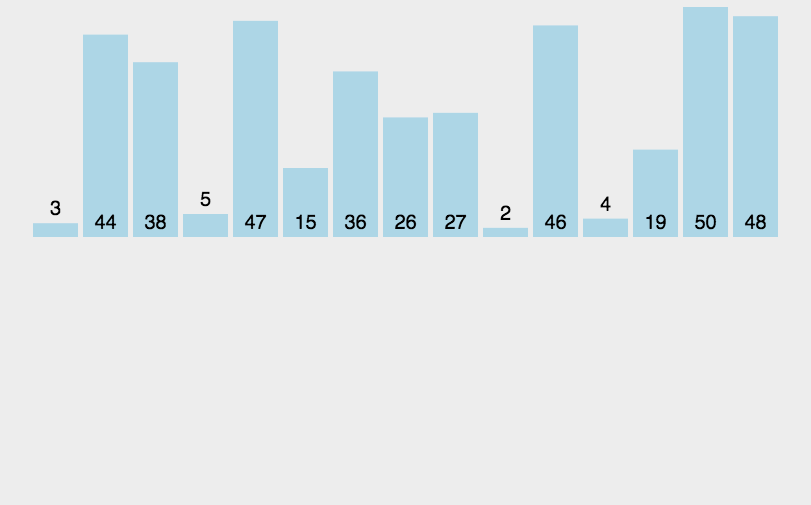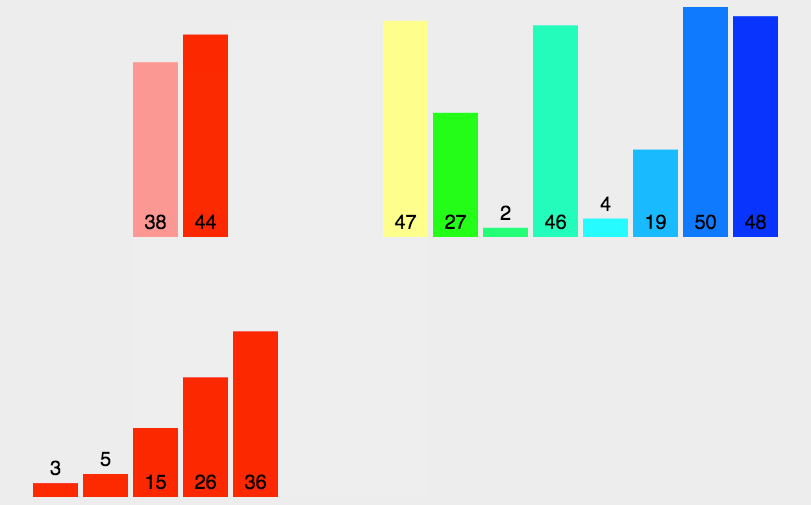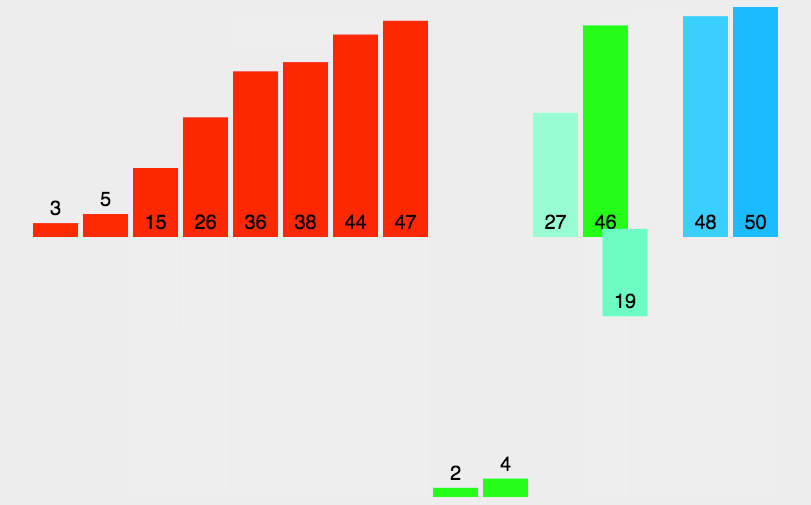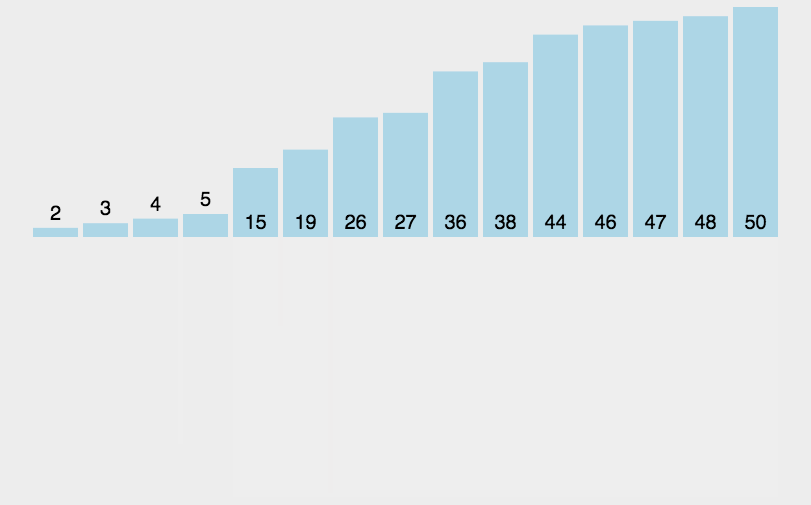
归并排序（MERGE-SORT）是利用归并的思想实现排序方法，该算法采用经典的分治（divide-and-conquer）策略（分治法将问题分（divide）成一些小的问题然后递归求解，而治（conquer）的阶段则将分的阶段得到的各答案“修补”在一起，即分而治之）。

2.动态效果图

归并排序（MergeSort）动图展示

3.相关详细文章
【Java数据结构与算法】归并排序

4.代码实现

public static void mergeSort(int[] arr,int left,int right,int[] temp) {
        if (left < right) {
            int mid = (left + right) /2;
            mergeSort(arr,left,mid,temp);
            mergeSort(arr,mid+1,right,temp);
            merge(arr,left,mid,right,temp);
        }
    }
	//合并的方法
    public static void merge(int[] arr,int left,int mid,int right,int[] temp) {
        int i = left;
        int j = mid + 1;
        int t = 0;
        while (i <= mid && j <= right) {
            if (arr[i] <= arr[j]) {
                temp[t] = arr[i];
                t += 1;
                i += 1;
            } else {
                temp[t] = arr[j];
                t += 1;
                j += 1;
            }
        }
        while (i <= mid) {
            temp[t] = arr[i];
            t += 1;
            i += 1;
        }
        while (j <= right) {
            temp[t] = arr[j];
            t += 1;
            j += 1;
        }
        t = 0;
        int tempLeft = left;
        while (tempLeft <= right) {
            arr[tempLeft] = temp[t];
            t += 1;
            tempLeft += 1;
        }
    }

7.基数排序（桶排序）

1.基本介绍

1. 基数排序（radix sort）属于“分配式排序”（distribution sort），又称“桶子法”（bucket sort）或bin sort，顾名思义，它是通过键值的各个位的值，将要排序的元素分配至某些“桶”中，达到排序的作用。
2. 基数排序法是属于稳定性的排序，基数排序法是效率最高的稳定性排序法
3. 基数排序（Radix Sort）是桶排序的扩展
4. 基数排序是1887年赫尔曼·何乐礼发明的。它是这样实现的：将整数按位数切割成为不同的数子，然后按照每个位数分别比较。

2.动态效果图

基数排序（RadixSort）动图展示

3.相关详细文章
【Java数据结构与算法】基数排序（桶排序）

4.代码实现

public static void radixSort(int[] arr) {
        int max = arr[0];
        for (int i = 1; i < arr.length; i ++) {
            if (arr[i] > max) {
                max = arr[i];
            }
        }
        int maxLength = (max + "").length();

        int[][] bucket = new int[10][arr.length];

        int[] bucketElementCounts = new int[10];

        for (int i = 0,n = 1;i < maxLength;i ++,n*=10) {
            for (int j = 0;j < arr.length;j ++) {
                int digitOfElement = arr[j] / n % 10;
                bucket[digitOfElement][bucketElementCounts[digitOfElement]] = arr[j];
                bucketElementCounts[digitOfElement] ++;
            }
            int index = 0;
            for (int k = 0;k < bucketElementCounts.length;k ++) {
                if (bucketElementCounts[k] != 0) {
                    for (int l = 0;l < bucketElementCounts[k];l ++) {
                        arr[index ++] = bucket[k][l];
                    }
                }
                bucketElementCounts[k] = 0;
            }
        }
    }

---

动图来源：像素博客园