2020牛客暑期多校训练营（第一场）题解 （A-J更新中）
A B-Suffix Array
题目链接
A B-Suffix Array
题目类型
字符串，特殊结论
题意
题解
代码
B Infinite Tree
C Domino
D Quadratic Form
E Counting Spanning Trees
F Infinite String Comparision
类型
字符串
链接
F Infinite String Comparision
题意
给你a、b两个字符串，要你比较a∞和b∞字符串的字典序大小，然后输出相应的符号>、<、=。
题解
错误思路
这里是我的第一个思路比较 0 0 0 ~ l c m ( l e n a , l e n b ) lcm(lena,lenb) lcm(lena,lenb)
REP(i, len){
if (a[i % lena] > b[i % lenb]) return 1;
else if (a[i % lena] < b[i % lenb]) return -1;
}
然而数据范围不允许我这么做 1 ≤ l e n a ≤ 1 e 5 1≤lena≤1e5 1≤lena≤1e5 1 ≤ l e n b ≤ 1 e 5 1≤lenb≤1e5 1≤lenb≤1e5，那么数据范围就有可能达到 9999900000 9999900000 9999900000，超时的情况就显而易见的了。
即使你比对的是
zz
zzzzz
会一样比对到10这个大小，显然是不必要的。
正确思路
公倍数的比对方法是多余的，那么我们应该比对到什么位置才是合适的呢？
在过题代码中， 2 ( l e n a + l e n b ) 2(lena+lenb) 2(lena+lenb) 与 l e n a + l e n b lena + lenb lena+lenb 与 l e n a + l e n b − g c d ( l e n a , l e n b ) lena + lenb - gcd(lena, lenb) lena+lenb−gcd(lena,lenb)都是通过的，那么哪种最为合理呢？
不妨举个例子
a1 a2
b1 b2 b3 b4 b5
比较
a1 a2 a1 a2 a1 a2、a1 a2 a1 a2
b1 b2 b3 b4 b5 b1、b2 b3 b4 b5
假设我需要比较到第6位置的时候，
其实已经满足很多条件了
也就是
- a1=b1
- a2=b2
- a1=b3
- a2=b4
- a1=b5
- 综上
- a1=b1=b3=b5,
- a2=b2=b4
- 也就是下一个判断的位置上就会得到a1=a2，那么所有都是相等
- 实际上只需要判断到 l e n a + l e n b − g c d ( l e n a , l e n b ) lena+lenb-gcd(lena, lenb) lena+lenb−gcd(lena,lenb)的位置
代码
int cmp(string a, string b){
int lena = SZ(a), lenb = SZ(b);
LL len = lena + lenb - gcd(lena, lenb);
REP(i, len){
if (a[i % lena] > b[i % lenb]) return 1;
else if (a[i % lena] < b[i % lenb]) return -1;
}
return 0;
}
int main(){
string a, b;
while(cin >> a >> b){
if (cmp(a, b) == 1) cout << ">\n";
else if (cmp(a, b) == -1) cout << "<\n";
else cout << "=\n";
}
}
还有一个方法就是成环对比
G BaXianGuoHai, GeXianShenTong
H Minimum-cost Flow
I 1 or 2
链接
1 or 2
类型
一般图最大匹配
题意
给你n个顶点，m条边，其中第i条边是在ai与bi之间，选择其中几条边保留，全部满足第i个顶点所有的度数为di
题解
看样例1
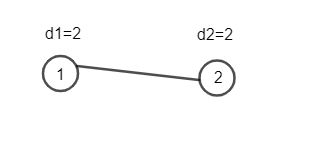
2 1
1 1
1 2
即2个顶点1条边，A、C分别都表示顶点，di 要求第一个顶点连接1条边，第二个顶点连接1条边
根据该图所示，我们选择AC边即满足题意d1 = 1,d2 = 1，所以输出yes
即本题需要做的就是图的匹配问题，通过选择边使得各个顶点度数与要求di度数相匹配。
这里题解中的意思是指拆点和拆边，
我们通过图示来看下样例吧
样例1
2 1
1 1
1 2
明显是成立的，所以直接输出Yes
样例2
2 1
2 2
1 2
样例2要求的度都是2，但又没有多余的边满足要求，所以就输出No
样例3
3 2
1 1 2
1 3
2 3
我们对样例3根据度数进行拆点以及拆边操作
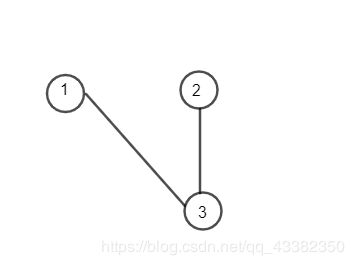
- 可能你会在图中看到两个 3 3 3实际上式将 3 3 3这个点按照度 d 3 = 2 d3=2 d3=2拆分成 3 3 3和 3 ’ 3’ 3’
- 4、5、6、7这几个出现的点可能会疑惑，实际上就是将边拆分成两个部分，即将1-3边拆分成4、5，而4与1是有关的、5与3是有关以此类推。
通过上图你就可以很好地进行匹配，以下是匹配成功的结果
拆完后进行一般图匹配就可了，kuangbin板子
代码
const int MAXN = 1111;
int N;
bool Graph[MAXN][MAXN]; //图
bool InQueue[MAXN],InPath[MAXN], InBlossom[MAXN];
int Start, Finish; //起始、结束
int Head, Tail;
int NewBase;
int Match[MAXN];
int Father[MAXN], Base[MAXN];
int Count = 0; //匹配成功的数量
int Queue[MAXN];
int n, m;
int d[MAXN];
VI V[MAXN]; //这个主要是用于我们的拆点操作, 大写区别于我们的点v
void CreateGraph(){
int u, v; RST(Graph); //对图进行初始化
//RD(n); // 输入顶点个数
//没有给出输入边的要求，就采用循环输入，直到输入文件结束
int tol = 1;
FOR_1(i, 1, n){
RD(d[i]);
V[i].clear();
FOR_1(j, 1, d[i]) V[i].PB(tol++);
}
FOR_1(i, 1, m){
int u, v; RD(u, v);
int x = tol++, y = tol++;
Graph[x][y] = Graph[y][x] = true;
for(int j = 0; j < V[u].size(); j++){
Graph[x][V[u][j]] = Graph[V[u][j]][x] = true;
}
for(int j = 0; j < V[v].size(); j++){
Graph[y][V[v][j]] = Graph[V[v][j]][y] = true;
}
}
N = tol - 1;
}
//队列的实现
void Push(int u){
Queue[Tail] = u;
Tail++;
InQueue[u] = true; //表示u点已经进入队列
}
int Pop(){
int res = Queue[Head];
Head++;
return res;
}
//寻找第一个匹配的顶点
int FindCommonAncestor(int u, int v){
RST(InPath); //初始化是否访问过路
while(true){
u = Base[u];
InPath[u] = true;
if(u == Start) break;
u = Father[Match[u]];
}
while(true){
v = Base[v];
if (InPath[v]) break;
v = Father[Match[v]];
}
return v;
}
void ResetTrace(int u){
int v;
while(Base[u] != NewBase){
v = Match[u];
InBlossom[Base[u]] = InBlossom[Base[v]] = true;
u = Father[v];
if (Base[u] != NewBase) Father[u] = v;
}
}
void BloosomContract(int u, int v){
NewBase = FindCommonAncestor(u, v);
memset(InBlossom, false, sizeof(InBlossom));
ResetTrace(u);
ResetTrace(v);
if (Base[u] != NewBase) Father[u] = v;
if (Base[v] != NewBase) Father[v] = u;
for(int tu = 1; tu <= N; tu++){
if (InBlossom[Base[tu]]){
Base[tu] = NewBase;
if (!InQueue[tu]) Push(tu);
}
}
}
void FindAugmentingPath(){
RST(InQueue);
RST(Father);
for(int i = 1; i <= N; i++){
Base[i] = i;
}
Head = Tail = 1;
Push(Start);
Finish = 0;
while(Head < Tail){
int u = Pop();
for(int v = 1; v <= N; v++){
if (Graph[u][v] && (Base[u] != Base[v]) && (Match[u] != v)){
if ((v == Start) || (Match[v] > 0 && Father[Match[v]] > 0)) BloosomContract(u, v);
else if (Father[v] == 0){
Father[v] = u;
if (Match[v] > 0) Push(Match[v]);
else {
Finish = v;
return ;
}
}
}
}
}
}
void AugmentPath()
{
int u,v,w;
u = Finish;
while(u > 0)
{
v = Father[u];
w = Match[v];
Match[v] = u;
Match[u] = v;
u = w;
}
}
void Edmonds()
{
memset(Match,0,sizeof(Match));
for(int u = 1; u <= N; u++)
if(Match[u] == 0)
{
Start = u;
FindAugmentingPath();
if(Finish > 0)AugmentPath();
}
}
void PrintMatch()
{
Count = 0;
for(int u = 1; u <= N;u++)
if(Match[u] > 0) Count++;
if(Count == N) OT("Yes");
else OT("No");
}
int main(){
//cout << false << 0 << '\n';
while(scanf("%d%d", &n, &m) == 2) { //点的个数，边的个数
CreateGraph();//建图
Edmonds();//Edmonds' algorithm 匹配
PrintMatch();
}
}
J Easy Integration
链接
J Easy Integration
类型
数学、规律
题意
∫ 1 0 ( x − x 2 ) n d x \int_{1}^{0}(x-x^2)^ndx ∫10(x−x2)ndx该积分式所能求得的结果可以化简为有理数 p q \frac{p}{q} qp,输出结果 p ∗ q − 1 p*q^{-1} p∗q−1 mod 998244353 998244353 998244353
题解
很明显
∫ 1 0 ( x − x 2 ) n d x = p q \int_{1}^{0}(x-x^2)^ndx=\frac{p}{q} ∫10(x−x2)ndx=qp是存在规律的，可以通过查询oeis或者是wolfram来进行猜测
也可以通过写出n=1,n=2,n=3来猜也是可以的。
推理
方法：n次分布积分
积分教学视频
取巧
查询1
查询2
积分可得
∫ 1 0 ( x − x 2 ) n d x = p q = n ! 2 ( 2 n + 1 ) ! \int_{1}^{0}(x-x^2)^ndx=\frac{p}{q}= \frac{{n!}^2}{(2n+1)!} ∫10(x−x2)ndx=qp=(2n+1)!n!2
化简后
p = n ! 2 p={n!}^2 p=n!2,
q = ( 2 n + 1 ) ! q=(2n+1)! q=(2n+1)!
分部
(( p p p mod 998244353 998244353 998244353) * ( q − 1 q^{-1} q−1 mod 998244353 998244353 998244353) mod 998244353 998244353 998244353
实际上求解的就是
( q − 1 q^{-1} q−1 mod 998244353 998244353 998244353)
这一部分，即求乘法逆元
ax + by = gcd(a, b) % mod
y = 0, x 是我们要求的解
ax = gcd(a, b) % mod
ax = 1 % mod
- qx = 1 mod (998244353)
- x = 1 / q mod (998244353)
所以x就是我们要求的解
void exgcd(int a, int b, int& x, int& y) {
if (b == 0) {
x = 1, y = 0;
return;
}
exgcd(b, a % b, y, x);
y -= a / b * x;
}
扩展欧几里得求解逆元在这里时间复杂度太高了，得用快速幂求逆元
- a x = 1 ax = 1 ax=1 mod b b b
- a x = a b − 1 ax = a^{b-1} ax=ab−1 mod b b b
- x = a b − 2 x = a^{b-2} x=ab−2 mod b b b
关于求解阶乘部分，那么我们就可以考虑到使用 快速乘 和 快速幂,然后得提前用数组存储，就可以减少重复的计算量，参考斐波那契
快速乘
inline ll mult_mod(ll a, ll b, ll m)
{
ll res = 0;
while(b){
if(b&1) res = (res+a)%m;
a = (a+a)%m;
b >>= 1;
}
return res;
}
inline ll mult_mod(ll a, ll b, ll m)
{
ll c = a*b-(ll)((long double)a*b/m+0.5)*m;
return c<0 ? c+m : c; //就是算的a*b%m;
}
两种都是对的，参考自快速乘原理及代码
一般第二种我是主要用于int128的乘
快速幂
inline LL qpow(LL a, LL b) {
int ans = 1;
a = (a % MOD + MOD) % MOD;
for (; b; b >>= 1) {
if (b & 1) ans = (a * ans) % MOD;
a = (a * a) % MOD;
}
return ans;
}
必须得要用快速幂。不然会超时。
取模乘
void MUL(int &a, int b){a = (LL)a * b % MOD;
代码
inline void MUL(LL &a, LL b){a = (LL)a * b % MOD;}
const int N = 2e6 + 2;
LL fa[N];
void init(){
fa[0] = fa[1] = 1;
FOR_1(i, 2, N) fa[i] = fa[i - 1] * i % MOD;
}
inline LL qpow(LL a, LL b) {
int ans = 1;
a = (a % MOD + MOD) % MOD;
for (; b; b >>= 1) {
if (b & 1) ans = (a * ans) % MOD;
a = (a * a) % MOD;
}
return ans;
}
int main(){
init();
for(LL n; scanf("%lld", &n)!=EOF; ){
LL q = fa[2 * n + 1];
LL p = fa[n] * fa[n] % MOD;
//cout << p << " " << q << '\n';
LL ans = qpow(q, (LL)MOD - 2);
//cout << ans << '\n';
MUL(ans, p);
OT(ans);
}
}