[概率统计]商务与经济统计知识点总结 Part 2
第三章 描述统计学2:数值方法
这章主要罗列一些常用的描述统计量。
位置的度量
也就是集中趋势的度量。
平均数
样本平均数
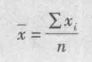
总体平均数

加权平均数

中位数
就是将一组数据按大小排序,找到中间数即可。
几何平均数
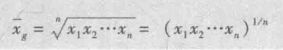
一般用于分析财务数据的增长率。几何平均数可以用于发生在所有时间长度的连续时期的任何数量的变化率。除了年变化率之外,几何平均数也常常用于发现季度、月、周以及天的平均变化率。
众数
众数就是出现次数最多的数据,可以存在也可以不存在,可以唯一也可以不唯一。
百分位数

四分位数
和上面公式相同,运用更加广泛一点,比如在异常值的识别这件事情上。
变异程度的度量
变异程度就是离散程度(离散趋势)的度量。
极差
极差 = 最大值 - 最小值
四分位数间距
IQR = Q3 - Q1
标准差
标准差为什么比方差适用范围更广?是因为标准差和原始数据的单位度量相同,标准差更容易与平均数和其他与原始数据有相同测量单位的统计量进行比较。
标准差系数
也叫变异系数,在比较具有不同标准差和不同平均数的变量的变异程度时,标准差系数是一个很有用的统计量。

分布形态、相对位置的度量以及异常值的检测
这些在 EDA 中其实都是比较常见的,这里看一下对于分布形态的度量。
分布形态
![[概率统计]商务与经济统计知识点总结 Part 2_第1张图片](http://img.e-com-net.com/image/info8/241e63a85fc84042aaf9adb7d4ec799a.jpg)
对于一个对称的分布,平均数和中位数是相等的。当数据的偏度为正时,通常平均数要比中位数大;当数据的偏度为负时,通常平均数要比中位数小。当数据严重偏离的时候,中位数是位置度量的首选。
z-分数
这个统计量是来衡量数据集中数据的相对位置(可以看作是标准化)。

z-分数往往被称为标准化数值。z-分数zi,能被解释为xi与平均数的距离是zi个标准差。
切比雪夫定理
感觉一般会在选择题里面考到,估算置信区间之类的。
切比雪夫定理的优点之一就是,她 适用于任何数据集而不论其数据分布的形状。
![[概率统计]商务与经济统计知识点总结 Part 2_第2张图片](http://img.e-com-net.com/image/info8/f5d78364e9cd4797a3eb2c17b42ef981.jpg)
经验法则
在实际应用中,当数据集近似服从正态分布(即呈对称的钟形或峰形分布时),就可以运用经验法则来确定与平均数的距离在某个特定个数的标准差之内的数据值所占的比例。
![[概率统计]商务与经济统计知识点总结 Part 2_第3张图片](http://img.e-com-net.com/image/info8/a8369c1b9df54dcfbefade6f797ffd4e.jpg)
异常值的检测
异常值可能是一个被错误记录的数据值,也可能是一个被错误包含在数据集中的观测值,也可能就是一个反常的数据值。
检测方法:
- z-分数可以用来确认异常值,通过经验法则来判断,建议把z-分数小于-3或大于+3的任何数值都是为异常值
- 以第一四分位数和第三四分位数以及四分位数间距为依据,首先计算上限和下限:

如果一个观测值的数值小于下限或大于上限,则被归类为异常值。
五数概括法和箱形图
这两个其实本质是一样的,就是一个是数值,一个是图示。
两变量关系的度量
协方差
即为两个变量之间线性关系的度量。
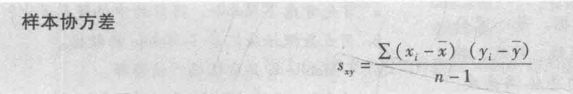

相关系数
![[概率统计]商务与经济统计知识点总结 Part 2_第7张图片](http://img.e-com-net.com/image/info8/ae1f0fb03b65420f8ef656ff5e1ba182.jpg)
![[概率统计]商务与经济统计知识点总结 Part 2_第8张图片](http://img.e-com-net.com/image/info8/c690458a18204ff98ceff51b4f729ab8.jpg)
相关系数要比协方差更容易度量变量之间的线性关系,因为相关系数是没有单位量纲的。
第四章 概率
概率就是对事件发生可能性的数值度量。
随机试验、计数法则和概率分配
随机试验:是一个过程,它所产生的实验结果是完全确定的。在每一次重复或者试验中,出现哪种结果完全由偶然性来决定。
样本空间:是试验所有结果组成的一个集合。
一种特定的试验结果被称为样本点,它是样本空间的一个元素。
事件及其概率
事件是样本点的一个集合。
事件的概率等于事件种所有样本点的概率之和。
概率的基本性质
P ( A ) = 1 − P ( A c ) P(A)=1-P(A^c) P(A)=1−P(Ac)
两个事件的并: A ∪ B A\cup B A∪B
两个事件的交: A ∩ B A\cap B A∩B
![[概率统计]商务与经济统计知识点总结 Part 2_第9张图片](http://img.e-com-net.com/image/info8/6280bedfd86a46058a01422deb6c6c78.jpg)
加法公式:
![]()
互斥时(一个发生另一个一定不会发生,即没有公共样本点)
![]()
条件概率
这个知识点还是蛮常考的,也是后面的贝叶斯定理的基础。
条件概率就是指在事件A发生的条件下事件B发生的可能性。
![[概率统计]商务与经济统计知识点总结 Part 2_第10张图片](http://img.e-com-net.com/image/info8/4c04d5a7bc6e4f12974503c8b6f7d7a8.jpg)
独立事件即事件A的概率不会因为事件B的发生与否而改变。
![[概率统计]商务与经济统计知识点总结 Part 2_第11张图片](http://img.e-com-net.com/image/info8/be901152748e446c9cadd24e64b3b38d.jpg)
乘法公式
![]()
贝叶斯定理
- 先验概率
- 后验概率
第五章 离散型概率分布
这一章和下一章的话笔试面试应该是比较常问的,比如说:**xxxx,是服从什么分布的?**或者说,让你求一些随机变量的期望和方差等等。
所以还是要仔细的记录一下。
随机变量
随机变量是对试验结果的数值描述。分为离散型和连续型。
离散型概率分布
随机变量的概率分布是描述随机变量取不同值得概率。对于离散型随机变量x,概率函数给出随机变量取每种值得概率,记作f(x)。
![[概率统计]商务与经济统计知识点总结 Part 2_第13张图片](http://img.e-com-net.com/image/info8/e5d31d4a52604d3cac6b72b845d62625.jpg)
离散型概率函数的基本条件
- f ( x ) ≥ 0 f(x)\geq 0 f(x)≥0
- ∑ f ( x ) = 1 \sum_{} f(x)=1 ∑f(x)=1
离散型均匀概率函数
f ( x ) = 1 n f(x)=\frac{1}{n} f(x)=n1
数学期望与方差
数学期望是指对随机变量中心位置的一种度量。
![]()
方差是用来描述随机变量取值的变异性。
![]()
随机变量之间的协方差
书上给了一种公式,应该是变形:
![]()
正常用的是下面这个:
![[概率统计]商务与经济统计知识点总结 Part 2_第14张图片](http://img.e-com-net.com/image/info8/9bbfd5e909bf4fab86735b4e726ae8a1.jpg)
随机变量之间的相关系数
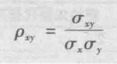

![[概率统计]商务与经济统计知识点总结 Part 2_第15张图片](http://img.e-com-net.com/image/info8/592adabb45dd49259b271a97f0d1abb5.jpg)
二项概率分布
二项试验
- 试验由一系列相同的n个试验组成
- 每次有两种可能的结果
- 每次试验成功的概率相同,用p来表示
- 试验相互独立
泊松概率分布
泊松试验的性质
- 在任意两个相等长度的区间上,事件发生的概率相等
- 事件在某一区间上是否发生与事件在其他区间上是否发生是独立的
超几何概率分布
这个分布描述了从有限N个物件(其中包含M个指定种类的物件)中抽出n个物件,成功抽出该指定种类的物件的次数(不放回)。
超几何概率分布与二项分布联系密切,这两种概率分布主要有两处不同:在超几何概率分布种,各次试验不是独立的,并且各次试验中成功的概率不相等。
![[概率统计]商务与经济统计知识点总结 Part 2_第18张图片](http://img.e-com-net.com/image/info8/531afbd383e7402aa2e4acb00891e0d4.jpg)
均值和方差
![[概率统计]商务与经济统计知识点总结 Part 2_第19张图片](http://img.e-com-net.com/image/info8/c58dd16dfbf242b48b48a075dfee8dbf.jpg)
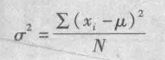

![[概率统计]商务与经济统计知识点总结 Part 2_第4张图片](http://img.e-com-net.com/image/info8/5c067f36fb3643b99a8dc6202ebb1f7f.jpg)
![[概率统计]商务与经济统计知识点总结 Part 2_第5张图片](http://img.e-com-net.com/image/info8/3c1f8be4dd6144b19c37e092c2cffd8d.jpg)
![[概率统计]商务与经济统计知识点总结 Part 2_第6张图片](http://img.e-com-net.com/image/info8/c3236f4b055946468d0e4ea666f8b7f9.jpg)

![[概率统计]商务与经济统计知识点总结 Part 2_第12张图片](http://img.e-com-net.com/image/info8/87bddc66647047a48ffbe64a9224379a.jpg)
![[概率统计]商务与经济统计知识点总结 Part 2_第16张图片](http://img.e-com-net.com/image/info8/3ee4f2b7586f4afa8297a01e5bef4823.jpg)
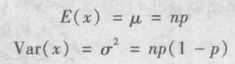
![[概率统计]商务与经济统计知识点总结 Part 2_第17张图片](http://img.e-com-net.com/image/info8/130ea03778cd4a5bbe2b118fb9bcaa65.jpg)