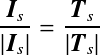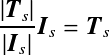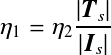GLSL中环境映射&菲涅尔反射效果

立方体贴图纹理与菲涅尔反射效果(Fresnel reflection)简介

↑

环境映射

光滑物体表面的鏡面反射效果及投射效果可以极大提升渲染场景的真实性。然而，为了正确模拟这类效果，需要用到光线追踪等非常耗时的方法。由于影响渲染物体的外在因素只有周围的远景，我们可以直接使用周围环境的远景贴图来实现这种效果。这种方法称为环境映射，一般分为贴在球体上的球形映射（Sphere maping），和贴在立方体上的立方体映射（Cube maping）。下图为立方体贴图纹理示例。

在OpenGL中

GL_TEXTURE_CUBE_MAP

用于声明立方体贴图纹理类型，用以下的设定，可以自动生成立方体贴图纹理用的贴图坐标。

glTexGeni(GL_S, GL_TEXTURE_GEN_MODE, GL_REFLECTION_MAP);
glTexGeni(GL_T, GL_TEXTURE_GEN_MODE, GL_REFLECTION_MAP);
glTexGeni(GL_R, GL_TEXTURE_GEN_MODE, GL_REFLECTION_MAP);

上述代码指定生成坐标模式为 GL_REFLECTION_MAP 。

下文使用GLSL计算反射折射向量，然后参照立方体贴图纹理实现反射折射效果。

计算反射方向向量

通过以下公式计算反射向量

计算反射向量的shader代码如下．

1 2 3 4 5 6

vec3 Reflection(vec3 I, vec3 N) { float cos_theta = dot(-I, N); vec3 R = 2*N*cos_theta+I; return (cos_theta > 0 ? normalize(R) : vec3(0.0)); }

另外，GLSL中有封装好的计算反射向量的函数reflect() ，

vec3 R = reflect(I, N);

↑

计算折射方向向量

根据斯涅尔定律(snell's law)，入射角与屈折角关系如下：

这里的是折射面两边的折射率．

根据上图，入射向量(), 折射向量, 法线向量 是单位向量。 , 的大小向量,如下

由此可得，

由于这里的和方向相同

因此，

根据斯涅尔定律，

带入上式得，

求得折射向量为，

计算折射向量的shader代码如下．

1 2 3 4 5 6 7

vec3 Refraction(vec3 I, vec3 N, float e) { float cos_theta = dot(-I, N); float cos_phi2 = 1.0-e*e*(1.0-cos_theta*cos_theta); vec3 T = e*(I+N*cos_theta)-N*sqrt(abs(cos_phi2)); return (cos_phi2 > 0 ? normalize(T) : vec3(0.0)); }

参数e指屈折率的比。 另外，也可以直接使用GLSL中封装好的计算折射向量的函数 refract() 

vec3 T = refract(I, N, e);

↑

菲涅尔反射效果

菲涅尔反射效果是指，不透明物体根据观察角度不同产生的反射和折射现象，比如你看向一个圆球，那圆球中心的反射较弱，靠近边缘较强，这就是“菲涅尔效应”。入射光強度中，代表反射，指折射。 这里的，是鏡面反射系数，折射系数。 一般无能量损失的情况下。

从观察者眼睛接收到光的角度考虑， 表面上的点从反射方向接收到的光的強度为， 折射方向的強度， 到达人眼的颜色为。 这个时候，根据菲涅尔反射公式，镜面反射系数为，

简便起见，这里根据Fernando et al.(1)的方法使用近似值计算．

其中bias值趋向于0时为折射效果，趋向1为反射效果。 GLSL代码如下。 顶点shader为，

1 2 3 4 5 6 7 8 9 10 11 12 13

varying vec4 vPos; varying vec3 vNrm; void main(void) { // vPos = gl_Vertex; // 顶点位置 vNrm = normalize(gl_NormalMatrix*gl_Normal); // 顶点法线 // 渲染顶点位置 gl_Position = ftransform(); }

片段shader代码为：

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49

varying vec4 vPos; varying vec3 vNrm; // GL uniform float fresnelBias; uniform float fresnelScale; uniform float fresnelPower; uniform float etaRatio; uniform vec3 eyePosition; uniform samplerCube envmap; vec4 lerp(vec4 a, vec4 b, float s) { return vec4(a+(b-a)*s); } /*! * Fresnel反射shander * @return 表面反射色 */ vec4 FresnelShading(void) { // 计算入射，反射，折射 vec3 N = normalize(vNrm); // 法线 vec3 I = normalize(vPos.xyz-eyePosition); // 入射 //vec3 R = reflect(I, N); // 反射 vec3 R = Reflection(I, N); // 反射 //vec3 T = refract(I, N, etaRatio); // 折射 vec3 T = Refraction(I, N, etaRatio); // 折射 // 反射因子计算 float fresnel = fresnelBias+fresnelScale*pow(min(0.0, 1.0-dot(I, N)), fresnelPower); // 获得反射环境色 vec4 reflecColor = textureCube(envmap, R); reflecColor.a = 1.0; // 计算折射环境色 vec4 refracColor; refracColor.rgb = textureCube(envmap, T).rgb; refracColor.a = 1.0; // 颜色合成 vec4 cout = lerp(refracColor, reflecColor, fresnel); cout.a = fresnel*0.5+0.5; return cout; }

将OpenGL中各参数及视点位置， 指定为立方体纹理贴图模式GL_TEXTURE_CUBE_MAP 生成对应坐标。

↑

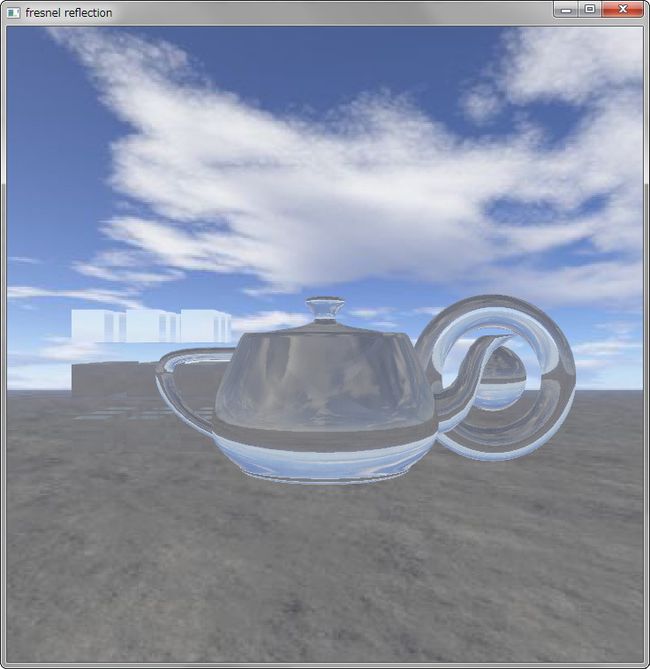
结果

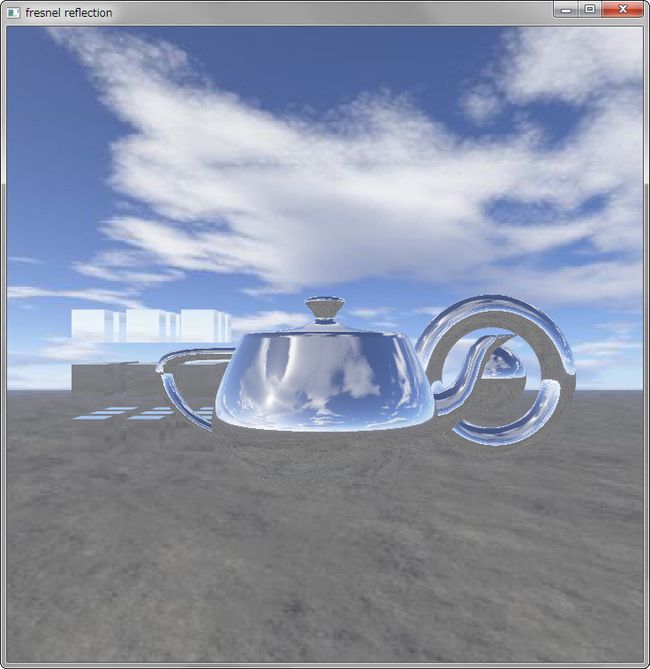etaRatio=0.8,bias=0.3	etaRatio=0.8,bias=1.0

(1)  R. Fernando and M. J. Kilgard, The Cg Tutorial: The Definitive Guide to Programmable Real-Time Graphics, Addison-Wesley Professional , 2003.