流形上的预积分

参考文献

• https://blog.csdn.net/qq_26682225/article/details/72649858
• On-Manifold Preintegration for Real-TimeVisual-Inertial Odometry
• 【泡泡机器人原创专栏】IMU预积分总结与公式推导（一）～（四）

一、预积分的由来

来协调imu数据和图像之间的关系。通过重新参数化[^1]来把关键帧之间的IMU数据积分成相对运动的约束，避免初始条件变化 [^2]造成的重复积分, 预积分的值并不是真实的测量值.

---

预积分与因子图结合, 增量式因子图

二、相关理论

• 基于滤波的方法能够快速的推断当前的状态量，但是精度会随着线性化误差的累积而恶化。
• 基于优化的完全平滑方法精度高一些，但计算量很大。
• 固定滞后的平滑方法（滑动窗）是一个折中。

---

采用了structless model(边际化)，这样可以不用延迟视觉信息的处理，同时可以多次线性化视觉测量模型。具体代码的实现整合在了gtsam4.0中

---

• 参加估计的pose number：

full smoothers: 所有的pose.

fixed-lag: 滑动窗口内的pose

filter: 最近的pose

• 代表不确定性的方法：

EKF: 协方差矩阵

信息滤波[^3]和smoothers: 信息矩阵

• 测量模型被线性化的次数：

standard EKF :1

smoothing appoach : 多次

---

fixed-lag和filter的方式相比对外点有更强的鲁棒性，fixed-lag在边际化的会使H矩阵变得稠密，为了保持稀疏性，需要丢掉一些测量点。此外两者都需要采用first estimate jacobian来线性化，来保持系统能观性不变，否则会引入错误的信息。

1. SLAM中的First-Estimates Jacobian。

对于一个系统，Observability性质（能观性），决定了这个系统在进行状态估计时，哪些自由度是可以被估计出来的。并且其能观性是不受估计方法（Closed-form 方法、EKF、或者Nonlinear Optimization等等）改变的。能观性通过Observability Matrix（能观性矩阵）体现，系统Unobservable的状态维数是这个矩阵零空间的维数。

比如，单目纯视觉SLAM里，尺度和6DOF的绝对位姿——总共7DOF，都是无法被估计。可以通过固定某一帧来确定6个自由度，但是尺度无法确定。

再比如Visual-Inertial系统里，在运动激励充分（足够多轴向有足够大的加速度/角速度）的情况下，尺度、滚转/俯仰角是可以被估计的，只剩下绝对偏航角、绝对位置无法获得，也就是说对于Visual-Inertial系统在合适的运动模式下Unobservable的维数是4。磁力计可以确定偏航角，加上固定某一帧可以确定相对位置。

不同的线性化状态点计算得到的系数矩阵（雅克比矩阵）会导致Observability Matrix（能观性矩阵）的零空间维数出现不一致（inconsistency），导致自由度不一样出现偏差。为了修正这个问题，提出了First Estimate Jacobian。用相同的状态点进行线性化计算就不会有这个问题了，具体来说，位姿采用propagated值而非updated值，landmark使用第一次估计值。First Estimate就是这个直观含义，即采用estimation from the first time。

理解不够透彻：可参考文献：

[1] Kelly, J., & Sukhatme, G. S. (2011). Visual-inertial sensor fusion: Localization, mapping and sensor-to-sensor self-calibration. The International Journal of Robotics Research, 30(1), 56-79

[3] Strasdat, H., Montiel, J. M. M., & Davison, A. J. (2010). Scale drift-aware large scale monocular SLAM. Robotics: Science and Systems VI.

[4] Huang, G. P., Mourikis, A. I., & Roumeliotis, S. I. (2009). A first-estimates Jacobian EKF for improving SLAM consistency. In Experimental Robotics(pp. 373-382). Springer Berlin Heidelberg.作者：

[8] Hermann, R., & Krener, A. J. (1977). Nonlinear controllability and observability. IEEE Transactions on automatic control, 22(5), 728-740.

---

预积分理论的贡献

• 使得测量与绝对位姿解耦
• 利用重力使得俯仰和横滚变得可观
• 与视觉结合使得bias可观

---

三、初步

a.黎曼几何概念

SO3群定义：
$$SO(3)=\{\mathbf{R}\in \mathbb{R}:{\mathbf{R}}^{\mathbf{T}}\mathbf{R}=\mathbf{I},det(\mathbf{R})=1\}.$$
他也代表着一个光滑的流形(manifold), 流形的切空间(tan)表示为李代数$\mathcal{S}O(3)$, 它与一个3维向量的3*3的反对称矩阵(向量加^表示)一致.
$${\omega }^{\wedge }={\left[\begin{array}{c}{\omega }_1\\ {\omega }_2\\ {\omega }_3\end{array}\right]}^{\wedge }=\left[\begin{array}{ccccc}0& & -{\omega }_3& & {\omega }_2\\ {\omega }_3& & 0& & -{\omega }_1\\ -{\omega }_2& & {\omega }_1& & 0\end{array}\right]\in \mathcal{S}\mathcal{O}(3).$$
他们之间的指数映射和对数映射如下：
$$\begin{array}{rlrlrlrl}Exp& :{\mathbb{R}}^3& \to & SO(3)& ;& \varphi & \to & exp({\varphi }^{\wedge })\\ Log& :SO(3)& \to & {\mathbb{R}}^3& ;& \mathbf{R}& \to & log(\mathbf{R})\end{array}$$
$Exp$映射:
$$Exp(\varphi )=I+\frac{sin(\Vert \varphi \Vert )}{\Vert \varphi \Vert }{\varphi }^{\wedge }+\frac{1-cos(\Vert \varphi \Vert )}{\Vert \varphi {\Vert }^2}({\varphi }^{\wedge }{)}^2$$
$Log$映射:
$$log(R)=\frac{\varphi \cdot ({\mathbf{R}-\mathbf{R}}^T)}{2sin(\varphi )},其中旋转角\varphi =co{s}^{-1}(\frac{tr(R)-1}{2})$$
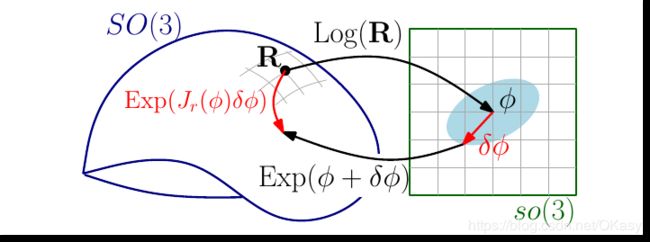
李群的乘法并不符合正常指数的运算法则，即不等于李代数的和，因此当变化量是微小量时使用BCH公式近似模型得到一阶近似：
$$Exp(\varphi +\delta \varphi )\approx Exp(\varphi )Exp(J_r(\varphi )\delta \varphi )$$
其中
$$J_r(\varphi )=\mathbf{I}-\frac{1-\cos (\parallel \varphi \parallel )}{\parallel \varphi {\parallel }^2}{\varphi }^{\wedge }+\frac{\mid \mid \varphi \mid \mid -\sin (\mid \mid \varphi \mid \mid )}{\mid \mid \varphi \mid {\mid }^3}({\varphi }^{\wedge }{)}^2$$
同理反之，乘法变加法也成立。

图中，$J_r(\varphi )$将切线空间中的累加增量与左侧的乘法增量相关联。
$$RExp(\varphi )R^T=exp(R{\varphi }^{\wedge }{R}^T)=Exp(R\varphi )$$

$$⟺Exp(\varphi )R=RExp(R^T\varphi ).$$

注意： 这里的$Exp$和$exp$是有区别的，大写的不需要^这个。

---

b.SO(3)中不确定性的描述

由前面知识可知：
$$\tilde{R}=RExp(ϵ),ϵ\sim N(0,\Sigma )$$
其中，$R$是不包含噪声的，$ϵ$是一个正态分布的小扰动.

我们对高斯扰动(3维高斯公式)进行积分:
$${\int }_{{\mathbb{R}}^3}p(ϵ)dϵ={\int }_{{\mathbb{R}}^3}\alpha e^{-\frac{1}{2}\parallel ϵ{\parallel }_{\Sigma }^2}dϵ=1,$$
其中$\alpha =1/\sqrt{(2\pi {)}^{3}det(\Sigma )}$, $\parallel ϵ{\parallel }_{\Sigma }^2={ϵ}^T{\Sigma }^{-1}ϵ$是马氏距离的平方.

当$\parallel ϵ\parallel <\pi$时, 根据式(8)可以推出$ϵ=Log(R^{-1}\tilde{R})$代入式(9)
$${\int }_{SO(3)}\beta (\tilde{R})e^{-\frac{1}{2}\parallel Log(R^{-1}\tilde{R}){\parallel }_{\Sigma }^2}d\tilde{R}=1,$$
$\beta (\tilde{R})$是一个归一化因子, 他等于$\beta (\tilde{R})=\alpha /\mid det(J(\tilde{R}))\mid$, 由于积分变量的变化$J(\tilde{R})\doteq J_r(Log(R^{-1}\tilde{R}))$

关于积分变量的推导：
$$\begin{array}{rl}\delta R& =Log(\frac{Exp(ϵ+\delta ϵ)}{Exp(ϵ)})\\ & =Log(\frac{Exp(ϵ)Exp(J_r\delta ϵ)}{Exp(ϵ)})\\ & =J_r\delta ϵ\end{array}$$
在SO(3)上的高斯扰动:
$$p(\tilde{R})=\beta (\tilde{R})e^{-\frac{1}{2}\parallel Log(R^{-1}\tilde{R}){\parallel }_{\Sigma }^2}$$
$ϵ$是小的协方差矩阵则, $\beta \approx \alpha$, 即$J(\tilde{R})=1$, 并且$\tilde{R}$接近R, 求其最大似然(log):
$$\mathcal{L}(R)=\frac{1}{2}\parallel Log(R^{-1}\tilde{R}){\parallel }_{\Sigma }^2+const=\frac{1}{2}\parallel Log({\tilde{R}}^{-1}R){\parallel }_{\Sigma }^2+const$$
其中const是$Log(\beta )$.

他的几何意义是SO(3)上的距离的平方, 不确定性权重为协方差的逆${\Sigma }^{-1}$.

c.流形上的高斯牛顿法

欧几里得空间的高斯牛顿法是迭代优化目标函数的二次近似（通常非凸），求解中通常简化为一系列的线性方程。

当变量属于流形时
$$\underset{x\in \mathcal{M}}{\min }f(x)$$
为了简化，我们只考虑一个变量时。

这里我们不能直接近似为$x$的二次函数。因为，

• 会使参数增多（9×3个）会导致欠定。
• 这么做会使结果不再是流形$\mathcal{M}$上的了，不满足SO(3)定义。

通常的做法是定义一个映射${\mathcal{R}}_x$, 它是由李代数(tan 空间)上的$\delta x$到$x\in \mathcal{M}$流形上附近值的一个映射.如下:
$$\underset{x\in \mathcal{M}}{\min }f(x)\Rightarrow \underset{\delta x\in {\mathbb{R}}^n}{\min }f(\mathcal{R}(\delta x)).$$
这种重新参数化叫做lifting.。这样就可以在欧几里得空间(也就是tan空间)进行优化，粗略地说当前估计定义在tan空间，而附近的增量是欧几里得空间。

在高斯牛顿框架下，求解当前估计的代价函数平方，得到最小时的李代数$\delta x^{\ast }$(tan空间),最终更新流形上的估计值
$$\hat{x}\leftarrow {\mathcal{R}}_{\hat{x}}(\delta x^{\ast })$$
这种方法是误差状态模型的基础和统一推广,通常是用于航空航天文献中的滤波方法.

本文中使用以下定义这种retraction(缩放?)
$${\mathcal{R}}_R(\varphi )=\mathrm{R}\mathrm{E}\mathrm{x}\mathrm{p}(\delta \varphi ),\delta \varphi \in {\mathbb{R}}^3$$

$${\mathcal{R}}_T(\delta \varphi ,\delta \mathbf{p})=(\mathrm{R}\mathrm{E}\mathrm{x}\mathrm{p}(\delta \varphi ),\mathbf{p}+\mathrm{R}\delta \mathbf{p}),\left[\begin{array}{cc}\delta \varphi & \delta \mathbf{p}\end{array}\right]\in {\mathbb{R}}^6$$

---

四、最大后验视觉惯导状态估计

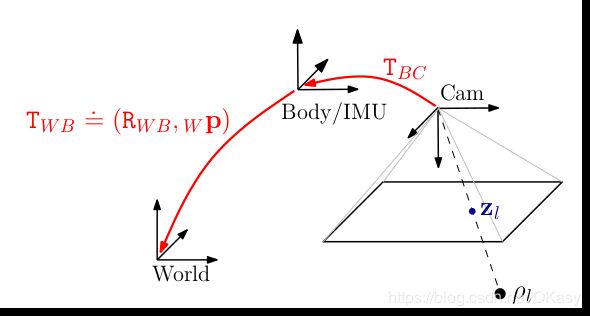
IMU的坐标系与机体坐标系一致,相机与机体系之间的变换关系已知.

系统状态变量为姿态,位置,速度,偏差:
$${\mathbf{x}}_i\doteq [{\mathbf{R}}_i,{\mathbf{p}}_i,{\mathbf{v}}_i,{\mathbf{b}}_i]$$
${\mathcal{K}}_k$表示到时间k所有关键帧的序列,我们估计所有关键帧的状态:
$${\mathcal{K}}_k\doteq \{{\mathrm{X}}_i{\}}_{i\in {\mathcal{K}}_k}$$
测量的关键帧图像${\mathcal{C}}_i$包含许多路标点$l$, 因此有观测值${\mathbf{z}}_{il}$. ${\mathcal{I}}_{ij}$表示两关键帧之间的IMU测量值. 因此测量可以表示为:
$${\mathcal{Z}}_k\doteq \{{\mathcal{C}}_i,{\mathcal{I}}_{ij}{\}}_{(i,j)\in {\mathcal{K}}_k}$$
${\mathcal{X}}_k$的后验概率:
$$\begin{gathered} p({\mathcal{X}}_k|{\mathcal{Z}}_k)\propto p({\mathcal{X}}_0)p({\mathcal{Z}}_k|{\mathcal{X}}_k)\stackrel{(a)}{=}p({\mathcal{X}}_0)\prod _{(i,j)\in {\mathcal{K}}_k}p({\mathcal{C}}_i,I_{ij}|{\mathcal{X}}_k) \\ \stackrel{(b)}{=}p({\mathcal{X}}_0)\prod _{(i,j)\in {\mathcal{K}}_k}p({\mathcal{I}}_{ij}|x_i,x_j)\prod _{i\in {\mathcal{K}}_k}\prod _{l\in {\mathcal{C}}_i}p(z_{il}|x_i) \end{gathered}$$
使用因子图来求解.

使用-log形式进行MAP估计, 可以写成残差像的和, 通俗说就是当前状态下预测值与测量值之间的不匹配度.
$$\begin{array}{rl}{\mathcal{X}}_k^{\ast }& \doteq arg\underset{{\mathcal{X}}_k}{\min }-{\log }_{e}p({\mathcal{X}}_k|{\mathcal{Z}}_k)\\ & =\arg \underset{{\mathcal{X}}_k}{\min }\Vert {\mathbf{r}}_0{\Vert }_{{\Sigma }_0}^2+\sum _{(i,j)\in {\mathcal{K}}_k}\Vert {\mathbf{r}}_{{\mathcal{I}}_{i,j}}{\Vert }_{{\Sigma }_{i,j}}^2+\sum _{i\in {\mathcal{K}}_k}\sum _{l\in {\mathcal{C}}_i}\Vert {\mathbf{r}}_{{\mathcal{C}}_{il}}{\Vert }_{{\Sigma }_{\mathcal{C}}}^2\end{array}$$

---

五、IMU模型和运动积分

陀螺仪测量模型:
$${}_B{\tilde{\omega }}_{WB}(t)={}_B{\omega }_{WB}(t)+{\mathbf{b}}^g(t)+{\eta }^g(t)$$
加速度计测量模型:
$${}_B\tilde{\mathbf{a}}(t)={\mathrm{R}}_{\mathrm{W}\mathrm{B}}^{\mathrm{T}}(t){(}_W\mathbf{a}(t){-}_W\mathbf{g})+{\mathbf{b}}^a(t)+{\eta }^a(t)$$
其中下标B表示机体坐标系, W表示世界坐标系(静止的), WB表示B系到W系转换. $\mathbf{b}$为缓慢变化的bias; $\eta$表示白噪声.

运动模型:
$$\dot{R_{\mathrm{W}\mathrm{B}}}={R_{\mathrm{W}\mathrm{B}}}_{\mathrm{B}}{\omega }_{\mathrm{W}\mathrm{B}}^{\wedge },{}_{\mathrm{W}}\dot{\mathbf{v}}{=}_{\mathrm{W}}\mathbf{a},{}_{\mathrm{W}}\dot{\mathbf{p}}{=}_{\mathrm{W}}\mathbf{v}$$

在时间段$[t,t+\Delta t]$上使用欧拉积分
$$\begin{array}{rl}& {\mathrm{R}}_{\mathrm{W}\mathrm{B}}(t+\Delta t)={\mathrm{R}}_{\mathrm{W}\mathrm{B}}(t)\mathrm{E}\mathrm{x}\mathrm{p}{(}_{\mathrm{B}}{\omega }_{\mathrm{W}\mathrm{B}}(t)\Delta t)\\ & {}_{\mathrm{W}}\mathbf{v}(t+\Delta t){=}_{\mathrm{W}}\mathbf{v}(t){+}_{\mathrm{W}}\mathbf{a}(t)\Delta t\\ & {}_{\mathrm{W}}\mathbf{p}(t+\Delta t){=}_{\mathrm{W}}\mathbf{p}(t){+}_{\mathrm{W}}\mathbf{v}(t)\Delta t+\frac{1}{2}{}_{\mathrm{W}}\mathbf{a}(t)\Delta t^2\end{array}\text{\hspace{1em}(28)}$$
将(25)(26)的测量模型公式代入得到:
$$\begin{array}{rl}& \mathrm{R}(t+\Delta t)=\mathrm{R}(t)\mathrm{E}\mathrm{x}\mathrm{p}((\tilde{\omega }(t)-{\mathbf{b}}^g(t)-{\eta }^{gd}(t))\Delta t)\\ & \mathbf{v}(t+\Delta t)=\mathbf{v}(t)+\mathbf{g}\Delta t+\mathrm{R}(t)(\tilde{\mathbf{a}}(t)-{\mathbf{b}}^a(t)-{\eta }^{ad}(t))\Delta t\\ & \mathbf{p}(t+\Delta t)=\mathbf{p}(t)+\mathbf{v}(t)\Delta t+\frac{1}{2}\mathbf{g}\Delta t^2+\frac{1}{2}\mathrm{R}(t)(\tilde{\mathbf{a}}(t)-{\mathbf{b}}^a(t)-{\eta }^{ad}(t))\Delta t^2\end{array}\text{\hspace{1em}(29)}$$
这里简化了符号的表示. 公式中我们假设$\mathrm{R}(t)$是恒定不变的, 这样会导致产生误差, 但当IMU频率较高时, 这个影响会大大减小. 当使用的IMU的频率较小时, 需要使用更高阶的数值积分方法.

其中的白噪声离散形式协方差为原噪声协方差的除以时间间隔$\Delta t$.

---

六、流形上的IMU预积分

IMU预积分的初衷，是希望借鉴纯视觉SLAM中图优化的思想，将帧与帧之间IMU相对测量信息转换为约束节点（载体位姿）的边参与到优化框架中。

• IMU预积分理论最大的贡献是对这些IMU相对测量进行处理，使得它与绝对位姿解耦（或者只需要线性运算就可以进行校正），从而大大提高优化速度。
• 这种优化架构还使得加计测量中不受待见的重力变成一个有利条件——重力的存在将使整个系统对绝对姿态（指相对水平地理坐标系的俯仰角和横滚角，不包括真航向）可观。要知道纯视觉VO或者SLAM是完全无法得到绝对姿态的。
• 两种传感器融合可以利用冗余测量（例如两种方式都可以求取相对位姿）来抑制累积误差。
• IMU和视觉这两种不同源的测量，也使得IMU的bias可观，从而可以在优化中被有效估计。
• 纯单目视觉缺乏绝对尺度的问题，也可以由惯性信息的引入而得以解决。

将两关键帧$i$和$j$之间的综合成一个复合的测量值, 叫preintegrated IMU measurement, 它约束连续关键帧之间的运动.

两个关键帧之间的关系如下:
$$\begin{array}{rl}& {\mathbf{R}}_j={\mathbf{R}}_i\prod _{k=i}^{j-1}\mathrm{E}\mathrm{x}\mathrm{p}(({\tilde{\omega }}_{\mathrm{k}}-{\mathrm{b}}_{\mathrm{k}}^{\mathrm{g}}-{\eta }_{\mathrm{k}}^{\mathrm{g}\mathrm{d}})\mathrm{\Delta }\mathrm{t}),\\ & {\mathbf{v}}_j={\mathbf{v}}_i+\mathbf{g}\Delta t_{ij}+\sum _{k=i}^{j-1}{\mathbf{R}}_k({\tilde{\mathbf{a}}}_k-{\mathbf{b}}_k^a-{\eta }_k^{ad})\Delta t\\ & {\mathbf{p}}_j={\mathbf{p}}_i+\sum _{k=i}^{j-1}[{\mathbf{v}}_k\Delta t+\frac{1}{2}\mathbf{g}\Delta t^2+\frac{1}{2}{\mathbf{R}}_k({\tilde{\mathbf{a}}}_k-{\mathbf{b}}_k^a-{\eta }_k^{ad})\Delta t^2]\end{array}\text{\hspace{1em}(30)}$$
从该公式(30)可以看出当初始值改变, 如${\mathbf{R}}_i$改变会导致每一个公式都需要重新计算. 为了解决这个缺陷, 给出不受线性化点影响的增量表达式:
$$\begin{array}{rl}& \Delta {\mathbf{R}}_{ij}={\mathbf{R}}_i^T{\mathbf{R}}_j=\prod _{k=i}^{j-1}\mathrm{E}\mathrm{x}\mathrm{p}(({\tilde{\omega }}_{\mathrm{k}}-{\mathrm{b}}_{\mathrm{k}}^{\mathrm{g}}-{\eta }_{\mathrm{k}}^{\mathrm{g}\mathrm{d}})\mathrm{\Delta }\mathrm{t}),\\ & \Delta {\mathbf{v}}_{ij}={\mathbf{R}}_i^T({\mathbf{v}}_j-{\mathbf{v}}_i-\mathbf{g}\Delta t_{ij})=\sum _{k=i}^{j-1}\Delta {\mathbf{R}}_{ik}({\tilde{\mathbf{a}}}_k-{\mathbf{b}}_k^a-{\eta }_k^{ad})\Delta t\\ & \Delta {\mathbf{p}}_{ij}={\mathbf{R}}_i^T({\mathbf{p}}_j-{\mathbf{p}}_i-{\mathbf{v}}_i\Delta t_{ij}-\frac{1}{2}\mathbf{g}\Delta t_{ij}^2)\\ & =\sum _{k=i}^{j-1}[\Delta {\mathbf{v}}_{ik}\Delta t+\frac{1}{2}\Delta {\mathbf{R}}_{ik}({\tilde{\mathbf{a}}}_k-{\mathbf{b}}_k^a-{\eta }_k^{ad})\Delta t^2]\end{array}\text{\hspace{1em}(31)}$$
最后的式子应用了等差数列求和公式推导, 证明如下:

这里的速度和位置$\Delta$值并不能代表真正的物理变化, 但却使得它与$i$时刻状态和重力独立, 能够直接根据惯性测量值计算出来. 这些值仍是Bias的函数, 假设Bias在两关键帧之间保持不变.

A. Preintegrated IMU Measurements

(1)$\Delta {\mathbf{R}}_{ij}$项

公式中包含的测量噪声使得MAP(最大后验估计)无法应用, 我们对公式进行变换, 把噪声独立出来, 使得log似然更容易获得. 假设$i$时刻bias已知且不变. 使用公式(6)和公式(9)将连乘展开后, 从第二个开始使用公式（8）进行两两合并, 之后再进行两两合并, 直到前面只有第一个Exp的连乘, 后面只有第二个Exp的复合连乘)_进行变换:
$$\begin{array}{rl}\Delta {\mathbf{R}}_{ij}& \stackrel{eq(6)}{\simeq }\prod _{k=i}^{j-1}[\mathrm{E}\mathrm{x}\mathrm{p}(({\tilde{\omega }}_{\mathrm{k}}-{\mathrm{b}}_{\mathrm{i}}^{\mathrm{g}})\mathrm{\Delta }\mathrm{t})\mathrm{E}\mathrm{x}\mathrm{p}(-{\mathrm{J}}_r^k{\eta }_k^{gd}\Delta t)]\\ & \stackrel{eq(9)}{=}\Delta {\tilde{\mathbf{R}}}_{ij}\prod _{k=i}^{j-1}\mathrm{E}\mathrm{x}\mathrm{p}(-\Delta {\tilde{\mathbf{R}}}_{k+1j}^T{\mathrm{J}}_r^k{\eta }_k^{gd}\Delta t)\\ & \doteq \Delta {\tilde{\mathbf{R}}}_{ij}\mathrm{E}\mathrm{x}\mathrm{p}(-\delta {\varphi }_{ij})\end{array}\text{\hspace{1em}(32)}$$
其中:
$$\begin{gathered} {\mathrm{J}}_r^k\doteq {\mathrm{J}}_r^k(({\tilde{\omega }}_k-b_i^g)\Delta t) \\ \Delta {\tilde{\mathbf{R}}}_{ij}=\prod _{k=i}^{j-1}\mathrm{E}\mathrm{x}\mathrm{p}(({\tilde{\omega }}_k-b_i^g)\Delta t)\text{\hspace{1em}(33)} \end{gathered}$$
$\delta {\varphi }_{ij}$定义为噪声.

总结:
$$\begin{gathered} \Delta {\mathbf{R}}_{ij}\doteq \Delta {\tilde{\mathbf{R}}}_{ij}\mathrm{E}\mathrm{x}\mathrm{p}(-\delta {\varphi }_{ij}) \\ \Delta {\tilde{\mathbf{R}}}_{ij}=\prod _{k=i}^{j-1}\mathrm{E}\mathrm{x}\mathrm{p}(({\tilde{\omega }}_k-b_i^g)\Delta t) \\ \mathrm{E}\mathrm{x}\mathrm{p}(-\delta {\varphi }_{ij})=\prod _{k=i}^{j-1}\mathrm{E}\mathrm{x}\mathrm{p}(-\Delta {\tilde{\mathbf{R}}}_{k+1j}^T{\mathrm{J}}_r^k{\eta }_k^{gd}\Delta t)\text{\hspace{1em}(34)} \end{gathered}$$

(2)$\Delta {\mathbf{v}}_{ij}$项

将式(32)代入(31)的速度预积分公式中, 对Exp进行一阶近似, 并且忽略高次微小量.得到:

$$\begin{array}{rl}\Delta {\mathbf{v}}_{ij}& =\sum _{k=i}^{j-1}\Delta {\tilde{\mathbf{R}}}_{ik}\mathrm{E}\mathrm{x}\mathrm{p}(-\delta {\varphi }_{ik})({\tilde{\mathbf{a}}}_k-{\mathbf{b}}_k^a-{\eta }_k^{ad})\Delta t\\ & =\sum _{k=i}^{j-1}[\Delta {\tilde{\mathbf{R}}}_{ik}(\mathbf{I}-\delta {\varphi }_{ik}^{\wedge })({\tilde{\mathbf{a}}}_k-{\mathbf{b}}_k^a)\Delta t-\Delta {\tilde{\mathbf{R}}}_{ik}{\eta }_k^{ad}\Delta t]\\ & =\sum _{k=i}^{j-1}[\Delta {\tilde{\mathbf{R}}}_{ik}({\tilde{\mathbf{a}}}_k-{\mathbf{b}}_k^a)\Delta t]+\sum _{k=i}^{j-1}[\Delta {\tilde{\mathbf{R}}}_{ik}({\tilde{\mathbf{a}}}_k-{\mathbf{b}}_k^a{)}^{\wedge }\delta {\varphi }_{ik}\Delta t-\Delta {\tilde{\mathbf{R}}}_{ik}{\eta }_k^{ad}\Delta t]\end{array}\text{\hspace{1em}(35)}$$
总结:
$$\begin{gathered} \Delta {\mathbf{v}}_{ij}\triangleq \Delta {\tilde{\mathbf{v}}}_{ij}-\delta {\mathbf{v}}_{ij} \\ \Delta {\tilde{\mathbf{v}}}_{ij}=\sum _{k=i}^{j-1}[\Delta {\tilde{\mathbf{R}}}_{ik}({\tilde{\mathbf{a}}}_k-{\mathbf{b}}_k^a)\Delta t] \\ \delta {\mathbf{v}}_{ij}=\sum _{k=i}^{j-1}[\Delta {\tilde{\mathbf{R}}}_{ik}{\eta }_k^{ad}\Delta t-\Delta {\tilde{\mathbf{R}}}_{ik}({\tilde{\mathbf{a}}}_k-{\mathbf{b}}_k^a{)}^{\wedge }\delta {\varphi }_{ik}\Delta t]\text{\hspace{1em}(36)} \end{gathered}$$

(3)$\Delta {\mathbf{p}}_{ij}$项

同上(34)和(36)式代入(31)中得到:
$$\begin{array}{rl}\Delta {\mathbf{p}}_{ij}& =\sum _{k=i}^{j-1}[(\Delta {\tilde{\mathbf{v}}}_{ik}-\delta {\mathbf{v}}_{ik})\Delta t+\frac{1}{2}\Delta {\tilde{\mathbf{R}}}_{ik}(\mathbf{I}-\delta {\varphi }_{ik}^{\wedge })({\tilde{\mathbf{a}}}_k-{\mathbf{b}}_k^a)\Delta t^2-\frac{1}{2}\Delta {\tilde{\mathbf{R}}}_{ik}{\eta }_k^{ad}\Delta t^2]\\ & =\sum _{k=i}^{j-1}[\Delta {\tilde{\mathbf{v}}}_{ik}\Delta t+\frac{1}{2}\Delta {\tilde{\mathbf{R}}}_{ik}({\tilde{\mathbf{a}}}_k-{\mathbf{b}}_k^a)\Delta t^2]\\ & +\sum _{k=i}^{j-1}[\frac{1}{2}\Delta {\tilde{\mathbf{R}}}_{ik}({\tilde{\mathbf{a}}}_k-{\mathbf{b}}_k^a{)}^{\wedge }\delta {\varphi }_{ik}\Delta t^2-\frac{1}{2}\Delta {\tilde{\mathbf{R}}}_{ik}{\eta }_k^{ad}\Delta t^2-\delta {\mathbf{v}}_{ik}\Delta t]\end{array}\text{\hspace{1em}(37)}$$
总结:
$$\begin{gathered} \Delta {\mathbf{p}}_{ij}\triangleq \Delta {\tilde{\mathbf{p}}}_{ij}-\delta {\mathbf{p}}_{ij} \\ \Delta {\tilde{\mathbf{p}}}_{ij}=\sum _{k=i}^{j-1}[\Delta {\tilde{\mathbf{v}}}_{ik}\Delta t+\frac{1}{2}\Delta {\tilde{\mathbf{R}}}_{ik}({\tilde{\mathbf{a}}}_k-{\mathbf{b}}_k^a)\Delta t^2] \\ \delta {\mathbf{p}}_{ij}=\sum _{k=i}^{j-1}[\frac{1}{2}\Delta {\tilde{\mathbf{R}}}_{ik}{\eta }_k^{ad}\Delta t^2-\frac{1}{2}\Delta {\tilde{\mathbf{R}}}_{ik}({\tilde{\mathbf{a}}}_k-{\mathbf{b}}_k^a{)}^{\wedge }\delta {\varphi }_{ik}\Delta t^2+\delta {\mathbf{v}}_{ik}\Delta t]\text{\hspace{1em}(38)} \end{gathered}$$
公式(34)(36)(38)代入公式(31)得到预积分测量模型，公式（39）左侧为预积分测量值(由IMU测量值和Bias的猜测估计值组成), 右侧为真值+预积分测量噪声.
$$\begin{gathered} \Delta {\tilde{\mathbf{R}}}_{ij}={\mathbf{R}}_i^{\mathrm{T}}{\mathbf{R}}_j\mathrm{E}\mathrm{x}\mathrm{p}(\delta {\varphi }_{ij}) \\ \Delta {\tilde{\mathbf{v}}}_{ij}={\mathbf{R}}_i^T({\mathbf{v}}_j-{\mathbf{v}}_i-\mathbf{g}\Delta t_{ij})+\delta {\mathbf{v}}_{\mathbf{i}\mathbf{j}} \\ \Delta {\tilde{\mathbf{p}}}_{ij}={\mathbf{R}}_i^T({\mathbf{p}}_j-{\mathbf{p}}_i-{\mathbf{v}}_i\Delta t_{ij}-\frac{1}{2}\mathbf{g}\Delta t_{ij}^2)+\delta {\mathbf{p}}_{ij}\text{\hspace{1em}(39)} \end{gathered}$$

B. Noise Propagation

希望使噪声符合高斯分布, 定义噪声向量:
$${\eta }_{ij}^{\Delta }\triangleq [\delta {\varphi }_{ij}^{\mathrm{T}},\delta {\mathbf{v}}_{ij}^{\mathrm{T}},\delta {\mathbf{p}}_{ij}^{\mathrm{T}}{]}^{\mathrm{T}}\sim \mathcal{N}(0_{9\times 1},{\Sigma }_{ij})\text{\hspace{1em}(40)}$$
对旋转量预积分噪声$\delta {\varphi }_{ij}$两端取-Log得到:
$$\delta {\varphi }_{ij}=-\mathrm{L}\mathrm{o}\mathrm{g}({\Pi }_{k=i}^{j-1}\mathrm{E}\mathrm{x}\mathrm{p}(-\Delta {\tilde{\mathbf{R}}}_{k+1j}^{\mathrm{T}}{\mathrm{J}}_r^k{\eta }_k^{gd}\Delta t))\text{\hspace{1em}(41)}$$
其中的${\eta }_k^{gd}$为微小量, 利用公式
$$\mathrm{L}\mathrm{o}\mathrm{g}(\mathrm{E}\mathrm{x}\mathrm{p}(\varphi )\mathrm{E}\mathrm{x}\mathrm{p}(\delta \varphi ))=\varphi +{\mathrm{J}}_{\mathrm{r}}^{-1}(\varphi )\delta \varphi \text{\hspace{1em}(42)}$$
得到
$$\delta {\varphi }_{ij}\simeq {\Sigma }_{k=i}^{j-1}\Delta {\tilde{\mathbf{R}}}_{k+1j}^{\mathrm{T}}{\mathrm{J}}_r^k{\mathbf{\eta }}_k^{gd}\Delta t\text{\hspace{1em}(43)}$$
证明:

由公式(43)可知, $\delta {\varphi }_{ij}$是${\mathbf{\eta }}_k^{gd}$线性组合, 因此也是零均值的高斯分布.

对于$\delta {\mathbf{v}}_{ij},\delta {\mathbf{p}}_{ij}$, 根据(36)(38)的增量项公式可知它们是$\delta {\varphi }_{ij}$和${\mathbf{\eta }}_k^{ad}$的线性组合, 因此也符合零均值的高斯分布.

B1. Iterative Noise Propagation

我们可以通过递推的形式求解${\mathbf{\eta }}_{ij}^{\Delta }$和其协方差${\mathbf{\Sigma }}_{ij}$.
$$\begin{array}{rl}\delta {\varphi }_{ij}& =\Delta {\tilde{\mathbf{R}}}_{jj-1}\delta {\varphi }_{ij-1}+{\mathbf{J}}_r^{j-1}{\mathbf{\eta }}_{j-1}^{gd}\Delta t\\ \delta {\mathbf{v}}_{ij}& =\delta {\mathbf{v}}_{ij-1}+\Delta {\tilde{\mathbf{R}}}_{ij-1}{\eta }_{j-1}^{ad}\Delta t-\Delta {\tilde{\mathbf{R}}}_{ij-1}({\tilde{\mathbf{a}}}_{j-1}-{\mathbf{b}}_i^a{)}^{\wedge }\delta {\varphi }_{ij-1}\Delta t\\ \delta {\mathbf{p}}_{ij}& =\delta {\mathbf{p}}_{ij-1}+\delta {\mathbf{v}}_{ij-1}\Delta t+\frac{1}{2}\Delta {\tilde{\mathbf{R}}}_{ij-1}{\mathbf{\eta }}_{j-1}^{ad}\Delta t^2-\frac{1}{2}\Delta {\tilde{\mathbf{R}}}_{ij-1}({\tilde{\mathbf{a}}}_{j-1}-{\mathbf{b}}_i^a{)}^{\wedge }\delta {\varphi }_{ij-1}\Delta t^2\end{array}\text{\hspace{1em}(44)}$$
其中第一个公式证明如下, 后两个公式即拆出一项即可.

定义IMU的测量噪声向量为
$${\mathbf{\eta }}_k^d=[{\mathbf{\eta }}_k^{gd},{\mathbf{\eta }}_k^{ad}]\text{\hspace{1em}(45)}$$
将式(44)写成矩阵形式:
$${\mathbf{\eta }}_{ij}^{\Delta }={\mathbf{A}}_{j-1}{\mathbf{\eta }}_{ij-1}^{\Delta }+{\mathbf{B}}_{j-1}{\mathbf{\eta }}_{j-1}^d\text{\hspace{1em}(46)}$$
其中
$${\mathbf{A}}_{j-1}=\left[\begin{array}{ccc}\Delta {\tilde{\mathbf{R}}}_{jj-1}& 0& 0\\ -\Delta {\tilde{\mathbf{R}}}_{ij-1}({\tilde{\mathbf{a}}}_{j-1}-{\mathbf{b}}_i^a{)}^{\wedge }\Delta t& \mathbf{I}& 0\\ -\frac{1}{2}\Delta {\tilde{\mathbf{R}}}_{ij-1}({\tilde{\mathbf{a}}}_{j-1}-{\mathbf{b}}_i^a{)}^{\wedge }\Delta t^2& \Delta t\mathbf{I}& \mathbf{I}\end{array}\right]\text{\hspace{1em}(47)}$$

$${\mathbf{B}}_{j-1}=\left[\begin{array}{cc}{\mathbf{J}}_r^{j-1}\Delta t& 0\\ 0& \Delta {\tilde{\mathbf{R}}}_{ij-1}\Delta t\\ 0& \frac{1}{2}\Delta {\tilde{\mathbf{R}}}_{ij-1}\Delta t^2\end{array}\right]\text{\hspace{1em}(48)}$$

据此可以求得预积分测量噪声的协方差矩阵:
$${\Sigma }_{ij}={\mathbf{A}}_{j-1}{\Sigma }_{ij-1}{\mathbf{A}}_{j-1}^T+{\mathbf{B}}_{j-1}{\Sigma }_{\eta }{\mathbf{B}}_{j-1}^T\text{\hspace{1em}(49)}$$

C. Incorporating Bias Updates

之前的计算都是在bias恒定的假设下进行的，但这是不现实的。重新计算预积分值会耗费大量的资源，因此使用一阶展开式来计算在bias增加一个小量时的预积分值的更新。
$$\begin{gathered} \Delta {\tilde{\mathbf{R}}}_{ij}({\hat{\mathbf{b}}}_i^g)\approx \Delta {\tilde{\mathbf{R}}}_{ij}({\overline{\mathbf{b}}}_i^g)\cdot \mathrm{E}\mathrm{x}\mathrm{p}\left(\frac{\partial \Delta {\overline{\mathbf{R}}}_{ij}}{\partial {\overline{\mathbf{b}}}^g}\delta {\mathbf{b}}_i^g\right) \\ \Delta {\tilde{\mathbf{v}}}_{ij}({\hat{\mathbf{b}}}_i^g,{\hat{\mathbf{b}}}_i^a)\approx \Delta {\tilde{\mathbf{v}}}_{ij}({\overline{\mathbf{b}}}_i^g,{\overline{\mathbf{b}}}_i^a)+\frac{\partial \Delta {\overline{\mathbf{v}}}_{ij}}{\partial {\overline{\mathbf{b}}}^g}\delta {\mathbf{b}}_i^g+\frac{\partial \Delta {\overline{\mathbf{v}}}_{ij}}{\partial {\overline{\mathbf{b}}}^a}\delta {\mathbf{b}}_i^a \\ \Delta {\tilde{\mathbf{p}}}_{ij}({\hat{\mathbf{b}}}_i^g,{\hat{\mathbf{b}}}_i^a)\approx \Delta {\tilde{\mathbf{v}}}_{ij}({\overline{\mathbf{b}}}_i^g,{\overline{\mathbf{b}}}_i^a)+\frac{\partial \Delta {\overline{\mathbf{p}}}_{ij}}{\partial {\overline{\mathbf{b}}}^g}\delta {\mathbf{b}}_i^g+\frac{\partial \Delta {\overline{\mathbf{p}}}_{ij}}{\partial {\overline{\mathbf{b}}}^a}\delta {\mathbf{b}}_i^a\text{\hspace{1em}(50)} \end{gathered}$$
为了求得雅克比系数，进行如下定义：
$$\begin{gathered} \Delta {\hat{\mathbf{R}}}_{ij}=\Delta {\tilde{\mathbf{R}}}_{ij}({\hat{\mathbf{b}}}_i^g),\Delta {\overline{\mathbf{R}}}_{ij}=\Delta {\tilde{\mathbf{R}}}_{ij}({\overline{\mathbf{b}}}_i^g) \\ \Delta {\hat{\mathbf{v}}}_{ij}=\Delta {\tilde{\mathbf{v}}}_{ij}({\hat{\mathbf{b}}}_i^g),\Delta {\overline{\mathbf{v}}}_{ij}=\Delta {\tilde{\mathbf{v}}}_{ij}({\overline{\mathbf{b}}}_i^g) \\ \Delta {\hat{\mathbf{p}}}_{ij}=\Delta {\tilde{\mathbf{p}}}_{ij}({\hat{\mathbf{b}}}_i^g),\Delta {\overline{\mathbf{p}}}_{ij}=\Delta {\tilde{\mathbf{p}}}_{ij}({\overline{\mathbf{b}}}_i^g)\text{\hspace{1em}(51)} \end{gathered}$$
使用与式(32)和(43)相同的方法，推导得到
$$\begin{array}{rl}\Delta {\hat{\mathbf{R}}}_{ij}& =\Delta {\tilde{\mathbf{R}}}_{ij}({\hat{\mathbf{b}}}_i^g)\\ & =\prod _{k=i}^{j-1}\mathrm{E}\mathrm{x}\mathrm{p}(({\tilde{\omega }}_k-b_i^g)\Delta t)\\ & =\prod _{k=i}^{j-1}\mathrm{E}\mathrm{x}\mathrm{p}(({\tilde{\omega }}_k-{\overline{b}}_i^g-\delta b_i^g)\Delta t)\\ & =\prod _{k=i}^{j-1}\mathrm{E}\mathrm{x}\mathrm{p}(({\tilde{\omega }}_k-{\overline{b}}_i^g)\Delta t)\mathrm{E}\mathrm{x}\mathrm{p}(-{\mathrm{J}}_r^k\delta {\mathbf{b}}_i^g\Delta t)\\ & =\Delta {\overline{\mathbf{R}}}_{ij}\prod _{k=i}^{j-1}\mathrm{E}\mathrm{x}\mathrm{p}(-\Delta {\tilde{\mathbf{R}}}_{k+1j}({\overline{\mathbf{b}}}_i{)}^{\mathrm{T}}{\mathrm{J}}_r^k\delta {\mathbf{b}}_i^g\Delta t)\\ & =\Delta {\overline{\mathbf{R}}}_{ij}\mathrm{E}\mathrm{x}\mathrm{p}(\sum _{k=i}^{j-1}-\Delta {\tilde{\mathbf{R}}}_{k+1j}({\overline{\mathbf{b}}}_i{)}^{\mathrm{T}}{\mathrm{J}}_r^k\delta {\mathbf{b}}_i^g\Delta t)\end{array}\text{\hspace{1em}(52)}$$
将其代入$\Delta {\hat{\mathbf{p}}}_{ij},\Delta {\hat{\mathbf{v}}}_{ij}$之中，并对Exp进行一阶近似可推导出其它雅克比系数。
$$\begin{array}{rl}\frac{\partial \Delta {\overline{\mathbf{R}}}_{ij}}{\partial {\overline{\mathbf{b}}}^g}& =-\sum _{k=i}^{j-1}[\Delta {\tilde{\mathbf{R}}}_{k+1j}({\overline{\mathbf{b}}}_i{)}^{\mathrm{T}}{\mathrm{J}}_r^k\Delta t]\\ \frac{\partial \Delta {\overline{\mathbf{v}}}_{ij}}{\partial {\overline{\mathbf{b}}}^a}& =-\sum _{k=i}^{j-1}\Delta {\overline{\mathbf{R}}}_{ik}\Delta t\\ \frac{\partial \Delta {\overline{\mathbf{v}}}_{ij}}{\partial {\overline{\mathbf{b}}}^g}& =-\sum _{k=i}^{j-1}\Delta {\overline{\mathbf{R}}}_{ik}({\overline{\mathbf{a}}}_k-{\overline{\mathbf{b}}}_i^a{)}^{\wedge }\frac{\partial \Delta {\overline{\mathbf{R}}}_{ik}}{\partial {\overline{\mathbf{b}}}^g}\Delta t\\ \frac{\partial \Delta {\overline{\mathbf{p}}}_{ij}}{\partial {\overline{\mathbf{b}}}^a}& =\sum _{k=i}^{j-1}\frac{\partial \Delta {\overline{\mathbf{v}}}_{ik}}{\partial {\overline{\mathbf{b}}}^a}\Delta t-\frac{1}{2}\Delta {\overline{\mathbf{R}}}_{ik}\Delta t^2\\ \frac{\partial \Delta {\overline{\mathbf{p}}}_{ij}}{\partial {\overline{\mathbf{b}}}^g}& =\sum _{k=i}^{j-1}\frac{\partial \Delta {\overline{\mathbf{p}}}_{ik}}{\partial {\overline{\mathbf{b}}}^g}\Delta t-\frac{1}{2}\Delta {\overline{\mathbf{R}}}_{ik}({\overline{\mathbf{a}}}_k-{\overline{\mathbf{b}}}_i^a{)}^{\wedge }\frac{\partial \Delta {\overline{\mathbf{R}}}_{ik}}{\partial {\overline{\mathbf{b}}}^g}\Delta t^2\end{array}$$

D. Preintegrated IMU Factors

预积分测量模型使用了大量的一阶近似和高斯分布近似，因此存在残差。残差是预积分的计算值（使用非IMU方法，如视觉）与测量值之间的差。优化最终的目的就是通过调整（lifting)导航状态使残差（的加权范数）最小化。

根据公式（39）可以得到残差的定义：
$${\mathbf{r}}_{{\mathcal{I}}_{ij}}\doteq [{\mathbf{r}}_{\Delta {\mathbf{R}}_{ij}}^{\mathrm{T}},{\mathbf{r}}_{\Delta {\mathbf{v}}_{ij}}^{\mathrm{T}},{\mathbf{r}}_{\Delta {\mathbf{p}}_{ij}}^{\mathrm{T}}{]}^{\mathrm{T}}\in {\mathbb{R}}^9\text{\hspace{1em}(53)}$$

$$\begin{array}{rl}{\mathbf{r}}_{\Delta {\mathbf{R}}_{ij}}& \doteq \mathrm{L}\mathrm{o}\mathrm{g}\left({\left(\Delta {\tilde{\mathbf{R}}}_{ij}({\overline{\mathbf{b}}}_i^g)\cdot \mathrm{E}\mathrm{x}\mathrm{p}\left(\frac{\partial \Delta {\overline{\mathbf{R}}}_{ij}}{\partial {\overline{\mathbf{b}}}^g}\delta {\mathbf{b}}_i^g\right)\right)}^{\mathrm{T}}{\mathbf{R}}_i^{\mathrm{T}}{\mathbf{R}}_j\right)\\ & =\mathrm{L}\mathrm{o}\mathrm{g}[(\Delta {\hat{\mathbf{R}}}_{ij}{)}^T\Delta {\mathbf{R}}_{ij}]\\ & \\ {\mathbf{r}}_{\Delta {\mathbf{v}}_{ij}}& \doteq {\mathbf{R}}_i^T({\mathbf{v}}_j-{\mathbf{v}}_i-\mathbf{g}\Delta t_{ij})\\ & -[\Delta {\tilde{\mathbf{v}}}_{ij}({\overline{\mathbf{b}}}_i^g,{\overline{\mathbf{b}}}_i^a)+\frac{\partial \Delta {\overline{\mathbf{v}}}_{ij}}{\partial {\overline{\mathbf{b}}}^g}\delta {\mathbf{b}}_i^g+\frac{\partial \Delta \overline{\mathbf{v}}}{\partial {\overline{\mathbf{b}}}^a}\\ & \\ & \\ {\mathbf{r}}_{\Delta {\mathbf{p}}_{ij}}& \\ & \\ & \end{array}$$