数据结构之静态查找(顺序表查找和有序表查找)C语言版
静态查找
- 前言
- 顺序表查找
- 顺序查找
- 哨兵查找
- 有序表查找
- 折半查找
- 插值查找
- 斐波那契查找
- 真正实现代码功能
- 运行结果
- 后记
前言
搜索引擎就是利用了查找的技术,查找方式按照操作方式有两大种,分别是静态查找和动态查找。静态查找只做查找,动态查找在查找过程中插入不存在的元素,删除已存在的元素。
本篇只讨论有关静态查找的内容
找不到返回-1
顺序表查找
顺序表查找分为顺序查找和优化的哨兵查找。
顺序查找
int Sequential_Search(int *a,int n,int key)
{
int i;
for(i=0;i<n;i++)
{
if(a[i]==key)
return i;
}
return -1;
}
哨兵查找
在优化的查找中,设置了一个哨兵,免去了查找过程中每次比较后都要判断查找位置是否越界。总数据较多时,效率提高很大
int Sequential_Search1(int *a,int n,int key)
{
int i;
a[-1] = key;//设置哨兵
i = n;
while(a[i]!=key)
{
i--;
}
return i;//返回-1则说明查找失败
}
有序表查找
有序表就是有排列顺序的表
折半查找适用于数据量较大的
插值查找适用于表长比较大,关键字分布广的
斐波那契适用于数据分布极端不均匀的
折半查找
int Binary_Search(int *a,int n,int key)
{
int low,high,mid;
low = 0;//定义最低下标为记录首位
high = 9;//定义最高下标为记录末尾
while(low<=high)
{
mid = (low+high)/2;//折半
if(key<a[mid])
high = mid-1;
else if(key>a[mid])
low = mid+1;
else
return mid;
}
return -1;
}
插值查找
插值查找的核心在于插值的计算公式。查找关键字key与查找表中最大最小记录的关键字比较后的查找方法。
代码就是折半查找中注释折半那一行替换为查找这一行就行了
mid = low+(high-low)*(key-a[low])/(a[high]-a[low]);//插值
斐波那契查找
斐波那契查找利用了黄金分割率原理实现
查找的核心在于:
当key = a[mid]时,查找成功;
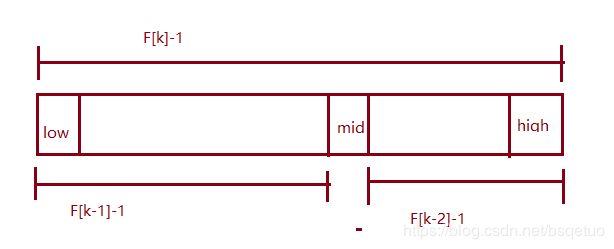
当key < a[mid]时,新范围是第low到mid-1个,此时范围个数为F[k-1]-1个;
当key 》 a[mid]时,新范围是第mid+1到high个,此时范围个数为F[k-2]-1个;
int Fibonacci_Search(int *a,int n,int key)
{
int F[30];
F[0] = 0;
F[1] = 1;
for(int m = 2;m<30;m++)
F[m] = F[m-1]+F[m-2];//斐波那契数组
int low,high,mid,i,k;
low = 0;//定义最低下标为记录首位
high = n;//定义最高下标为记录末尾
k = 0;
while(n>F[k]-1)//记录n位于斐波那契数列的位置
k++;
for(i=n;i<F[k]-1;i++)//将不满的数值补全
a[i] = a[n];
while(low<=high)
{
mid = low+F[k-1]-1;//计算当前分隔的下标
if(key<a[mid])
{
high = mid-1;//最高下标调整到mid-1处
k = k-1;//斐波那契下标减一位
}
else if(key>a[mid])//若查找记录大于分隔记录
{
low = mid+1;//最低下标调整到mid+1处
k = k-2;//斐波那契下标减一二位
}
else
{
if(mid<=n)
return mid;
else
return n;//若mid=n,说明是补全数值,返回n
}
}
return -1;
}
}
真正实现代码功能
花了较长时间把这些代码的功能实现了。
注意创建一个比较自由的数组,我们可以用顺序表的结构体来表示数组,但是还有一种方法,与结构体表示有异曲同工之妙,首先创建一个数组,然后往其中填充数据,再用一个子函数求出数据长度。
顺序表数据是自己填充
有序表是系统自带,长度固定为9
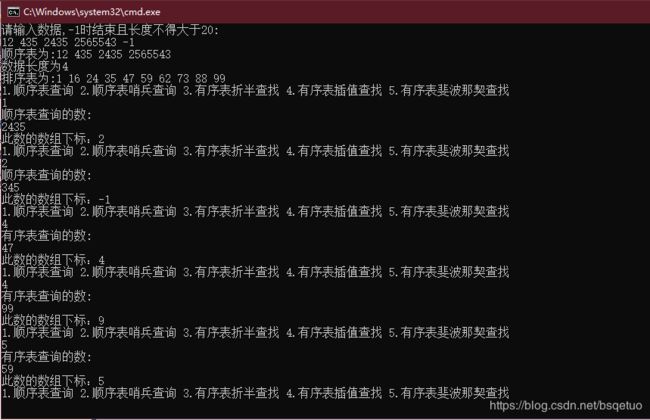
#include运行结果
后记
本篇确实是只用一片代码柔和了五个算法,实在有些罗嗦,但是功能确实是全部实现的。
今天的内容就是静态查找的基本操作及其内容,喜欢我的多多支持哦~