一分钟速学 | NMS, IOU 与 SoftMax

非极大抑制

NMS的英文是Non-maximum suppression的缩写。

简单的说，就是模型给出了多个重叠在一起的候选框，我们只需要保留一个就可以了。其他的重叠的候选框就删掉了，效果可见下图：

交并比

IoU的英文全称Intersection over Union，就是两个候选框区域的交集面积比上并集的面积，用下图可以理解：

hard-NMS

hard-nms其实就是经典版本的NMS的方法。就是根据模型给出每个box的置信度从大到小进行排序，然后保留最大的，删除所以与这个最大置信度的候选框的IoU大于阈值的其他候选框。

举个例子吧，现在有4个候选框：
(box1,0.8),(box2,0.9),
(box3,0.7),(box4,0.5)

我们把这四个候选框按照置信度从大到小排序：
box2>box1>box3>box4

现在我们保留置信度最大的候选框box2,然后计算剩下三个box与box2之间的IoU，如果IoU大于一个事先设置的阈值，那么就删除这个box。假设,阈值是0.5:
IoU(box1,box2)=0.1<0.5，保留；IoU(box3,box2)=0.7<0.5，删除；IoU(box4,box2)=0.2<0.5，保留；

现在还有box1和box4，然后再重复上面的过程，排序，然后删除。

下面是python实现的hard-NMS：

def hard_nms(box_scores, iou_threshold, top_k=-1, candidate_size=200):
    """
    Args:
        box_scores (N, 5): box的集合，N为框的数量，5即4(位置信息)+1(可能为物体的概率)
        iou_threshold: 我们用IOU标准去除多余检测框的阈值
        top_k: 保留多少个计算后留下来的候选框，如果为-1则全保留
        candidate_size: 参与计算的boxes数量
    Returns:
         picked: 经过nms计算后保留下来的box
    """
    scores = box_scores[:, -1]                # 首先我们取出box中的最后一个元素也就是当前box检测到物体的概率
    boxes = box_scores[:, :-1]                # 取出box中的四个坐标(左上、右下)
    picked = []  
    _, indexes = scores.sort(descending=True) # 按照降序排列所有的物体的概率，得到排序后在原数组中的索引信息 indexes
    indexes = indexes[:candidate_size]        # 只保留前 candidate_size 个 boxes 其余的不考虑了
    while len(indexes) > 0:
        current = indexes[0]                  # 每次取出当前在 indexes 中 检测到物体概率最大的一个 
        picked.append(current.item())         # 将这个最大的存在结果中
        if 0 < top_k == len(picked) or len(indexes) == 1:
            break
        current_box = boxes[current, :]       # 当前第一个也就是最高概率的box
        indexes = indexes[1:]                
        rest_boxes = boxes[indexes, :]        # 剩下其余的box
        iou = iou_of(                         # 将当前的box与剩下其余的boxes用IOU标准进行筛选
            rest_boxes,
            current_box.unsqueeze(0),
        )
        indexes = indexes[iou <= iou_threshold]# 保留与当前box的IOU小于一定阈值的boxes，

    return box_scores[picked, :]

如何计算iou的面积呢？实现方法在下面：

def area_of(left_top, right_bottom) -> torch.Tensor:
    """Compute the areas of rectangles given two corners.

    Args:
        left_top (N, 2): left top corner.
        right_bottom (N, 2): right bottom corner.

    Returns:
        area (N): return the area.
    """
    hw = torch.clamp(right_bottom - left_top, min=0.0)
    return hw[..., 0] * hw[..., 1]


def iou_of(boxes0, boxes1, eps=1e-5):
    """Return intersection-over-union (Jaccard index) of boxes.

    Args:
        boxes0 (N, 4): ground truth boxes.
        boxes1 (N or 1, 4): predicted boxes.
        eps: a small number to avoid 0 as denominator.
    Returns:
        iou (N): IoU values.
    """
    overlap_left_top = torch.max(boxes0[..., :2], boxes1[..., :2])
    overlap_right_bottom = torch.min(boxes0[..., 2:], boxes1[..., 2:])

    overlap_area = area_of(overlap_left_top, overlap_right_bottom)
    area0 = area_of(boxes0[..., :2], boxes0[..., 2:])
    area1 = area_of(boxes1[..., :2], boxes1[..., 2:])
    return overlap_area / (area0 + area1 - overlap_area + eps)

soft-NMS

在密集目标检测任务中，hard-NMS会有一些问题，看下面的例子：

两个物体重叠起来了，但是根据hard-NMS绿色的框会被掉。

Soft-NMS就改动了一个地方。 在判断最高的置信度的box和其他box的IoU的时候增加了一个系数，可以更好的选择哪些才是多余的box。

对于hard-NMS来说，\(iou(M,b_i)的时候，保留，大于等于的时候删除，\(s\)表示置信度：

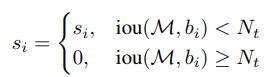
对于soft-NMS来说，\(iou(M,b_i)的时候，保留，大于的时候削减：

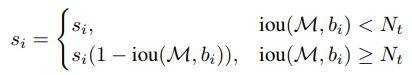
可以看出来，hard-NMS对于IoU大于阈值的候选框，直接把其置信度变成0，这样就相当于删除了这个box；但是soft-NMS的会根据IoU的大小，去适当的削减置信度，从而留下一些余地。

【如何削减】
这里有两种方法来降低重叠候选框的置信度：

1. \(s=s(1-iou(M,b))\)简单的线性衰减；
2. \(s = se^{-\frac{iou(M,b)^2}{\sigma}}\)指数衰减。其中sigma是常数，一般是0.5.

第二种方法更为常见。

---

下面是python来实现的soft-NMS，其实跟hard-NMS相比，就多了一行代码罢了：

def soft_nms(box_scores, score_threshold, sigma=0.5, top_k=-1):
    """Soft NMS implementation.

    References:
        https://arxiv.org/abs/1704.04503
        https://github.com/facebookresearch/Detectron/blob/master/detectron/utils/cython_nms.pyx

    Args:
        box_scores (N, 5): boxes in corner-form and probabilities.
        score_threshold: boxes with scores less than value are not considered.
        sigma: the parameter in score re-computation.
            scores[i] = scores[i] * exp(-(iou_i)^2 / simga)
        top_k: keep top_k results. If k <= 0, keep all the results.
    Returns:
         picked_box_scores (K, 5): results of NMS.
    """
    picked_box_scores = []
    while box_scores.size(0) > 0:
        max_score_index = torch.argmax(box_scores[:, 4])
        cur_box_prob = torch.tensor(box_scores[max_score_index, :])
        picked_box_scores.append(cur_box_prob)
        if len(picked_box_scores) == top_k > 0 or box_scores.size(0) == 1:
            break
        cur_box = cur_box_prob[:-1]
        box_scores[max_score_index, :] = box_scores[-1, :]
        box_scores = box_scores[:-1, :]
        ious = iou_of(cur_box.unsqueeze(0), box_scores[:, :-1])

        # 以下这句是新加的，如果没有这句就是Hard-NMS了
        box_scores[:, -1] = box_scores[:, -1] * torch.exp(-(ious * ious) / sigma) 

        box_scores = box_scores[box_scores[:, -1] > score_threshold, :]
    if len(picked_box_scores) > 0:
        return torch.stack(picked_box_scores)
    else:
        return torch.tensor([])