基于Kalman filter 的北斗卫星三维坐标后数据处理

基于Kalman filter 的北斗卫星三维坐标后数据处理

Kalman filter 基本介绍

1. 1.  应用场景？

模型内事件状态转换是线性的，噪声干扰是高斯的

公式表示：

P（Xt|Xt-1）=N(AX+B,Q)   Xt=AXt-1+B+W

P(Yt|Xt)=N(HX+C,R)  Yt=HX+C+V     W  ,V meet Normal distribution( 0,sigma)

制定H ，降维 我们只需要某一个维度状态

P(Xt|Y1,Y2,….Yt)

  

 

 

 

1. 2.  Kalman filter求什么？

求（Xt|Y1*Y2*Y3….Yt）的性质。

Xt是某事物t时刻真实的状态。Yt是t时刻观察事物状态的观测值。

 我们已知前t个的时刻的观测值， 计算t时刻 隐状态的某些 参数。

比如概率P，均值E(Xt_bar)，方差Var（Xt_bar）。

3.基本思想：

没有真值， 只有传感器的观测值，具有对目标系统建立数学模型获得预期值。

我们要用预期值和观测值来逼近真值。

举个例子：

 

 

蓝色的模型预期值，红色的传感器的值，我们通过把两个正态分布乘起来，计算概率密度函数的均值，来寻找最佳估计。

为什么是乘（1*1=1）？ 为什么能乘（∫fdx=1）？

 

 

 

 

 

 

4.算法步骤

 

4.1列方程模型

 匀速直线运动+干扰， （静止则速度为0），模型中的加速度和速度不是恒定的，是参数迭代计算出来的。 

 初值是我们定义的。 但是初值作用不是很大，经过少量迭代即可趋于稳定。

 

 

 

P是FX的协方差矩阵，

Qk是状态转移协方差矩阵。联系两个连续离散时刻的协方差矩阵（实际上是噪声Δw的协方差矩阵，后面说明），Qk参数可以以自己调节。

F是两个连续时刻状态的过渡矩阵。，wk是扰动。

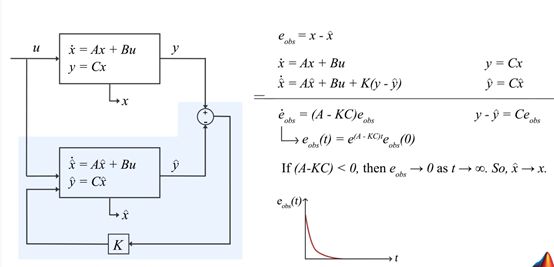
4.2 寻找迭代 闭环

如何保证能算法收敛？

 

 

u为输入，y输出模型预期值。Y_hat是 真实传感器的值。

收敛的条件：调整KC使得A-KC小于0，指数函数就会随着时间收敛。

 

 

我把K取值为负数。结果误差是7*10^304 mm

 

 

我们写出P（xt|y1：t-1），P（xt|y1：t）的值。

为什么要写这个P（xt|y1：t-1）P（xt|y1：t）？HMM，当转移矩阵，测量矩阵，初始概率确定后，模型就确定的。我们写出P（xt|y1：t-1），P（xt|y1：t）是量化。

 

 

 

公式（2），冒号代表从1到t-1，

p(xt|y1:t−1)代表预测，已知t-1时刻的观测值，求xt时刻的状态。

当有了p(yt|xt)中的yt 后，就可以对p(xt|y1:t)中的 Xt实现更新。

注意prediction   中 p(xt|y1:t) 与 p(xt|y1:t−1)已经 实现递归

p(xt|y1:t−1)满足高斯分布，p(yt|xt)满足高斯分布，高斯乘以高斯结果还是高斯分布。所以p(xt|y1:t)也是高斯的。

 

 

 

 

说明算法处理同一组数据，结果只能限定在一个范围内，绝对没有一组数据是结果一样的。

 

 

 

实际上：t=1时刻有  P（X1|Y1）~N(μ_hat_1，sigma_hat_1)  update

t=2时刻有  P（X2|Y1）~N(μ_bar_2，sigma_bar_2)   prediction

P（X2|Y1，Y2）~N(μ_bar_2，sigma_bar_2)    update

 

同样的：t时刻

P(Xt|Y1,Y2,,,Yt)~ N(μ_hat_t，sigma_hat_t)   update

P(Xt|Y1:Yt)~N(μ_bar_t，sigma_bar_t))  prediction

 

我们要做什么？把参数设置好了时候，每次不断求update 和prediction的值，

也就是如何从上一次高斯的两个参数mean和var，得到下一次高斯的两个参数mean和var。

 

 

 

 

 

 

 

 

 

分别对随机变量X和线性变换后的随机变量AX计算mean和var。

 

 

Q噪声的Δw的协方差矩阵，是Δw，不是w的协方差，所以不为0。

Q我在计算时取为定值。（实际上不应该是定值）噪声一定会变，可是我没办法预估。

通过观测定值效果也很不错。我已经把结果震荡限制在1mm内。

有了P（xt|y1：t-1），P（xt|y1：t）后，就可以求t时刻状态值的mean和var。

第一种计算方法：

 

另一种计算的方法：

 

 

思路相同：利用模型预期值和测量值，来寻找最佳估计值

已知状态的Xt，观测的Yt，边缘分布。

如何求Xt，Yt的边缘分布呢？--结果显然是高斯的。查表套公式即可。

 

求出XY期望的mean和var ，

 

 

同样的还是会得到这三个公式。

 

实际上是mean和var两个公式。

 

 

（注意K是被推导的）只不过要查表应用随机变量乘积的高斯分布获取乘积的pdf。

4.3迭代更新。

4.4 观测滤波结果，不符合预期则调整参数

 

 

 

 

1. 中值滤波数据预处理，
2. 计算预处理后的标准差 ，作为加入噪声的参考值，使用计算预处理后的均值，作为代替真值的参考值（大样本均值思想）
3. 设置模型初始条件，设置参数，模型确定了，P,H参数是固定的。F中第一行第二个元素是时间，我对照表格取一分钟，F的其他参数也是固定的。联系两个FX的协方差的矩阵Q的取值很大程度影响误差，R是调整预期值与传感器值权重的参数，相信预期值多，则把R调小些，反之亦反。

 

 

 

1. 开始迭代，输入卡拉曼滤波公式，开始接待计算误差。
2. 目前参数我已经调整到 把结果稳定在了1mm内
3. 部分结果展示，经过少量迭代，结果趋于稳定。

 

 

横轴是位置，纵轴是速度，很明显，速度是非常接近0.

1. 同时也观察不同Q值对误差影响，Q值建议调成大于1

 

 

 

计划：进行实时数据检验算法准确性，效果不佳，尝试非线性非高斯粒子滤波。

考虑到天气等原因影响，尝试使用参数学习，找出最佳参数，实现参数自适应。

 

 

 

 

欢迎大家随时打断我，感谢大家提出自己的见解!