Matlab线性/非线性规划优化算法(3)
本文开始介绍非线性规划函数fmincon的用法,这个函数解决的典型问题是:
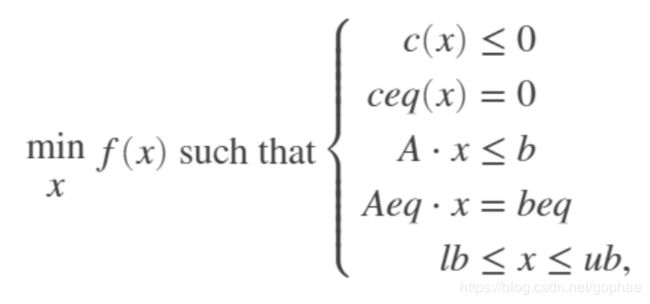
和上两个规划很相似,有等式约束和不等式约束,在不等式约束中还可以存在非线性约束。可以有的写法如下:
>> help fmincon
fmincon - Find minimum of constrained nonlinear multivariable function
Nonlinear programming solver.
x = fmincon(fun,x0,A,b)
x = fmincon(fun,x0,A,b,Aeq,beq)
x = fmincon(fun,x0,A,b,Aeq,beq,lb,ub)
x = fmincon(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon)
x = fmincon(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon,options)
x = fmincon(problem)
[x,fval] = fmincon(___)
[x,fval,exitflag,output] = fmincon(___)
[x,fval,exitflag,output,lambda,grad,hessian] = fmincon(___)
See also fminbnd, fminsearch, fminunc, optimoptions, optimtool
Documentation for fmincon
有兴趣的可以每个都试一下,但我就只用最复杂的那个作为示例来展示了:
我们现在有这个一个非线性优化函数:fun = @(x)100*(x(2)-x(1)2)2 + (1-x(1))^2;需要优化,我手动的给他添加了所有种类的约束:
包括:1, 不等式约束Ax ≤ b : A = [1,2]; b = 1;
2, 等式约束: Aeqx = beq Aeq = [2,1]; beq = 1;
3, 自变量上下界: lb = [0,0]; ub = [1,2];
4,非线性约束: nonlinear, 这个函数内部意思就是自变量被约束在一个圆的内部。
5,优化参数设置: 我要求他使用内点法求解,如果不设置,matlab默认求解器应该是sqp
最后给出代码:
%% the use of fmincon
clc
clear all
x0 = [0.1 0.3];
A = [1,2];
b = 1;
Aeq = [2,1];
beq = 1;
lb = [0,0.2];
ub = [0.5,0.8];
nonlcon = @nonlinear;
options = optimoptions('fmincon','Display','iter','Algorithm','interior-point');
fun = @(x)100*(x(2)-x(1)^2)^2 + (1-x(1))^2;
[x,fval,exitflag,output,lambda,grad,hessian] ...
= fmincon(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon,options)
%% fmincon with gradient
clc
clear all
x0 = [0.1 0.3];
A = [1,2];
b = 1;
Aeq = [2,1];
beq = 1;
lb = [0,0.2];
ub = [0.5,0.8];
nonlcon = @nonlinear;
options = optimoptions('fmincon','Display','iter','Algorithm','interior-point','SpecifyObjectiveGradient',true);
fun = @rosenbrockwithgrad;
[x,fval,exitflag,output,lambda,grad,hessian] ...
= fmincon(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon,options)
%% fmincon using problem structure
options = optimoptions('fmincon','Display','iter','Algorithm','interior-point');
problem.options = options;
problem.solver = 'fmincon';
problem.objective = @(x)100*(x(2)-x(1)^2)^2 + (1-x(1))^2;
problem.x0 = [0.1 0.3];
problem.A = [1,2];
problem.b = 1;
problem.beq = 1;
problem.Aeq = [2,1];
problem.lb = [0,0.2];
problem.ub = [0.5,0.8];
problem.nonlcon = @unitdisk;
[x,fval,exitflag,output,lambda,grad,hessian] ...
= fmincon(problem)
这里面有三种写法,第一种就是普通写法,第二种我们刻意加入了梯度信息,第三种我们使用了problem structure写法,其中需要调用的函数,下面给出,
function [c,ceq] = unitdisk(x)
c = (x(1)-1/3)^2 + (x(2)-1/3)^2 - (1/3)^2;
ceq = [ ];
end
function [c,ceq] = nonlinear(x)
c = (x(1)-1/3)^2 + (x(2)-1/3)^2 - (1/3)^2;
ceq = [];
end
function [f,g] = rosenbrockwithgrad(x)
% Calculate objective f
f = 100*(x(2) - x(1)^2)^2 + (1-x(1))^2;
if nargout > 1 % gradient required
g = [-400*(x(2)-x(1)^2)*x(1)-2*(1-x(1));
200*(x(2)-x(1)^2)];
end
按照我的要求,输出了相关中间变量和参数:
First-order Norm of
Iter F-count f(x) Feasibility optimality step
0 3 9.220000e+00 5.000e-01 1.687e+01
1 6 1.474360e+00 1.666e-01 2.284e+01 2.382e-01
2 9 5.478845e-01 0.000e+00 1.247e+01 8.242e-02
3 12 5.792800e-01 0.000e+00 4.196e-01 2.670e-03
4 15 5.437391e-01 0.000e+00 2.104e-02 3.037e-03
5 18 5.215088e-01 0.000e+00 5.309e-03 2.037e-03
6 21 5.202050e-01 0.000e+00 2.002e-04 1.232e-04
7 24 5.200021e-01 0.000e+00 2.017e-06 1.921e-05
Local minimum found that satisfies the constraints.
Optimization completed because the objective function is non-decreasing in
feasible directions, to within the value of the optimality tolerance,
and constraints are satisfied to within the value of the constraint tolerance.
<stopping criteria details>
x =
0.4000 0.2000
fval =
0.5200
exitflag =
1
output =
struct with fields:
iterations: 7
funcCount: 24
constrviolation: 0
stepsize: 1.9214e-05
algorithm: 'interior-point'
firstorderopt: 2.0170e-06
cgiterations: 0
message: '↵Local minimum found that satisfies the constraints.↵↵Optimization completed because the objective function is non-decreasing in ↵feasible directions, to within the value of the optimality tolerance,↵and constraints are satisfied to within the value of the constraint tolerance.↵↵↵↵Optimization completed: The relative first-order optimality measure, 2.521268e-07,↵is less than options.OptimalityTolerance = 1.000000e-06, and the relative maximum constraint↵violation, 0.000000e+00, is less than options.ConstraintTolerance = 1.000000e-06.↵↵'
lambda =
struct with fields:
eqlin: 3.8000
eqnonlin: [0×1 double]
ineqlin: 9.8723e-06
lower: [2×1 double]
upper: [2×1 double]
ineqnonlin: 2.2644e-05
grad =
-7.6000
8.0001
hessian =
136.0238 -148.9825
-148.9825 205.5079
关于如何具体描述优化问题,matlab doc里面给出了详细解释,可以去参考如果有问题,下面我摘出最重要的部分:
fun — Function to minimize
Initial point, specified as a real vector or real array. Solvers use the number of elements in, and size of, x0 to determine the number and size of variables that fun accepts.
‘interior-point’ algorithm — If the HonorBounds option is true (default), fmincon resets x0 components that are on or outside bounds lb or ub to values strictly between the bounds.
‘trust-region-reflective’ algorithm — fmincon resets infeasible x0 components to be feasible with respect to bounds or linear equalities.
‘sqp’, ‘sqp-legacy’, or ‘active-set’ algorithm — fmincon resets x0 components that are outside bounds to the values of the corresponding bounds.
Example: x0 = [1,2,3,4]
A — Linear inequality constraints
Linear inequality constraints, specified as a real matrix. A is an M-by-N matrix, where M is the number of inequalities, and N is the number of variables (number of elements in x0). For large problems, pass A as a sparse matrix.
A encodes the M linear inequalities
A*x <= b,
where x is the column vector of N variables x(, and b is a column vector with M elements.
For example, to specify
x1 + 2x2 ≤ 10
3x1 + 4x2 ≤ 20
5x1 + 6x2 ≤ 30,
enter these constraints:
A = [1,2;3,4;5,6];
b = [10;20;30];
b — Linear inequality constraints
Linear inequality constraints, specified as a real vector. b is an M-element vector related to the A matrix. If you pass b as a row vector, solvers internally convert b to the column vector b(. For large problems, pass b as a sparse vector.
b encodes the M linear inequalities
A*x <= b,
where x is the column vector of N variables x(, and A is a matrix of size M-by-N.
For example, to specify
x1 + 2x2 ≤ 10
3x1 + 4x2 ≤ 20
5x1 + 6x2 ≤ 30,
enter these constraints:
A = [1,2;3,4;5,6];
b = [10;20;30];
Aeq — Linear equality constraints
Linear equality constraints, specified as a real matrix. Aeq is an Me-by-N matrix, where Me is the number of equalities, and N is the number of variables (number of elements in x0). For large problems, pass Aeq as a sparse matrix.
Aeq encodes the Me linear equalities
Aeq*x = beq,
where x is the column vector of N variables x(, and beq is a column vector with Me elements.
For example, to specify
x1 + 2x2 + 3x3 = 10
2x1 + 4x2 + x3 = 20,
enter these constraints:
Aeq = [1,2,3;2,4,1];
beq = [10;20];
beq — Linear equality constraints
Linear equality constraints, specified as a real vector. beq is an Me-element vector related to the Aeq matrix. If you pass beq as a row vector, solvers internally convert beq to the column vector beq(. For large problems, pass beq as a sparse vector.
beq encodes the Me linear equalities
Aeq*x = beq,
where x is the column vector of N variables x(, and Aeq is a matrix of size Me-by-N.
For example, to specify
x1 + 2x2 + 3x3 = 10
2x1 + 4x2 + x3 = 20,
enter these constraints:
Aeq = [1,2,3;2,4,1];
beq = [10;20];
nonlcon — Nonlinear constraints
Nonlinear constraints, specified as a function handle or function name. nonlcon is a function that accepts a vector or array x and returns two arrays, c(x) and ceq(x).
c(x) is the array of nonlinear inequality constraints at x. fmincon attempts to satisfy
c(x) <= 0 for all entries of c.
ceq(x) is the array of nonlinear equality constraints at x. fmincon attempts to satisfy
ceq(x) = 0 for all entries of ceq.
For example,
x = fmincon(@myfun,x0,A,b,Aeq,beq,lb,ub,@mycon)
where mycon is a MATLAB function such as
function [c,ceq] = mycon(x)
c = … % Compute nonlinear inequalities at x.
ceq = … % Compute nonlinear equalities at x.
If the gradients of the constraints can also be computed and the SpecifyConstraintGradient option is true, as set by
options = optimoptions(‘fmincon’,‘SpecifyConstraintGradient’,true)
then nonlcon must also return, in the third and fourth output arguments, GC, the gradient of c(x), and GCeq, the gradient of ceq(x). GC and GCeq can be sparse or dense. If GC or GCeq is large, with relatively few nonzero entries, save running time and memory in the interior-point algorithm by representing them as sparse matrices. For more information, see Nonlinear Constraints.
最后还有点值得一说,要注意输出宗量exitflag, 并不是所有解都是可行解,迭代退出的原因就是由exitflag指代的,只有flag>0的时候,迭代才算是正常完成。具体的指代如下:
All Algorithms:
1
First-order optimality measure was less than options.OptimalityTolerance, and maximum constraint violation was less than options.ConstraintTolerance.
0
Number of iterations exceeded options.MaxIterations or number of function evaluations exceeded options.MaxFunctionEvaluations.
-1
Stopped by an output function or plot function.
-2
No feasible point was found.
All algorithms except active-set:
2
Change in x was less than options.StepTolerance and maximum constraint violation was less than options.ConstraintTolerance.
trust-region-reflective algorithm only:
3
Change in the objective function value was less than options.FunctionTolerance and maximum constraint violation was less than options.ConstraintTolerance.
active-set algorithm only:
4
Magnitude of the search direction was less than 2*options.StepTolerance and maximum constraint violation was less than options.ConstraintTolerance.
5
Magnitude of directional derivative in search direction was less than 2*options.OptimalityTolerance and maximum constraint violation was less than options.ConstraintTolerance.
interior-point, sqp-legacy, and sqp algorithms:
-3
Objective function at current iteration went below options.ObjectiveLimit and maximum constraint violation was less than options.ConstraintTolerance.