特征值和特征向量

前言

特征值和特征向量是计算机视觉以及机器学习中常常会用到的概念，比如PCA（主成分分析）等算法。这篇文章中会记录一些我自己对矩阵的特征值和特征向量的理解以及学习笔记。

从简单实例理解

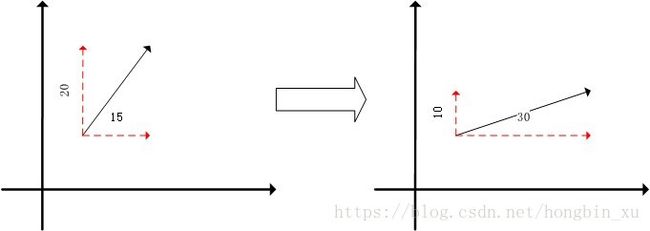
如上图是一个简单的示意图，在两个坐标系中给出了两个向量（黑色），红色表示其沿两个坐标轴方向正交分解得到的向量，数字表示向量的长度。一般来说矩阵可以表示某一种线性变化，比如，在这个例子中，向量都是2维的。图中两个向量的变换关系很容易看出，水平方向乘以2，垂直方向乘以0.5。那么，可以定义一个变换矩阵 A A ：

A=[2000.5] A = [ 2 0 0 0.5 ]

通过变换矩阵 A A ，可以将左图的向量 v1→=(x1,y1) v 1 → = ( x 1 , y 1 ) 变换为右图的向量 v2→=(x2,y2) v 2 → = ( x 2 , y 2 ) ： v2→=Av1→ v 2 → = A v 1 → 。

乘上换矩阵 A A ，等价于对向量 v1→ v 1 → 做了一个线性变换，使其变换为向量 v2→ v 2 → ，方向和长度都改变了。但是，图中的几个红色的向量，仅仅发生了长度上的变换，而方向没有发生变换，像这种向量不受到线性变换的影响，也被称作矩阵 A A 的特征向量。通过这几个特征向量（红色）的关系，我们也可以逆推出（唯一确定）方阵 A A 。

定义

上面的例子仅仅是围绕着二维的情况讨论的，也比较直观，而实际应用中，矩阵的维度远远不止2维，很可能大得多。前面提到的概念可以通过类比来辅助理解，下面是定义：

Av⃗ =λv⃗ (1) (1) A v → = λ v →

上式中， A A 是一个 n×n n × n 的矩阵， λ λ 是矩阵 A A 的一个特征值， x x 是一个 n n 维的向量，而 x x 也是矩阵 A A 的特征值 λ λ 所对应的特征向量。

在上面的例子中是对向量做正交分解，类比来理解，我们同样也可以将向量投影在 n n 个方向上。在这 n n 个方向中的某一个方向上，所有这个方向上的向量都是特征向量，而特征值 λ λ 表示的就是线性变化（乘以矩阵 A A ）对特征向量的影响。与二维的情况类似，这些特征向量的“方向”不会受到线性变换的影响，“长度”会乘以某个标量值，而这个标量值也正是 λ λ 。在特征向量 v⃗  v → 上的线性变化 A A 完全由特征值 λ λ 定义。这仅仅是一个直观上的理解，没有理解也无所谓，不影响使用。

Av⃗ −λv⃗ =0⇒(A−λI)v⃗ =0(2) (2) A v → − λ v → = 0 ⇒ ( A − λ I ) v → = 0

其中， I I 是与矩阵 A A 具有相同维度的单位矩阵。

有式子2可以知道，如果 v⃗  v → 不是零向量，那么 (A−λI)=0 ( A − λ I ) = 0 ，即 (A−λI) ( A − λ I ) 不可逆。

如果一个方阵不可逆，这意味着它的行列式一定为0。

因此有下式：

Det(A−λI)=0(3) (3) D e t ( A − λ I ) = 0

通过求解式子3即可以求出矩阵 A A 的特征向量和特征值。

特征分解

求到特征值和特征向量有什么用？

就围绕最开始那个二维的例子来说吧，其中的向量做正交分解得到了红色标注的2个特征向量，原始向量被分成了两个特征，而对向量做线性变换（乘以矩阵 A A ）变成了分别给两个特征向量乘以一个对应的特征值，最后再组合成新的向量。扩展到高维的情况也是同理。求特征值和特征向量的作用就是将矩阵 A A 的特征分解。

假设矩阵 A A 是一个 n×n n × n 的方阵，如果求到了矩阵 A A 的 n n 个特征值 {λ1≤λ2≤...≤λn} { λ 1 ≤ λ 2 ≤ . . . ≤ λ n } ，以及这 n n 个特征值对应的特征向量 {ω1,ω2,...,ωn} { ω 1 , ω 2 , . . . , ω n } ，矩阵 A A 就可以用下式表示特征分解：

AW=WΣ⇒A=WΣW−1(4) (4) A W = W Σ ⇒ A = W Σ W − 1

其中， W W 表示 n n 个特征向量组成的矩阵， Σ Σ 表示以 n n 个特征值为主对角线的 n×n n × n 维的矩阵。

W=[w1w2...wn](5) (5) W = [ w 1 w 2 . . . w n ]

Σ=⎡⎣⎢⎢⎢λ10...00λ2...0............00...λn⎤⎦⎥⎥⎥(6) (6) Σ = [ λ 1 0 . . . 0 0 λ 2 . . . 0 . . . . . . . . . . . . 0 0 . . . λ n ]

（注： AW=WΣ A W = W Σ 就是将前面特征值与特征向量的定义式 Aωi=λiωi A ω i = λ i ω i 拼起来了，还有注意 W W 要左乘 Σ Σ ）

一般来说，我们会将 W W 的 n n 个特征向量标准化，即满足 ||ωi||2=1 | | ω i | | 2 = 1 或 ωTiωi=1 ω i T ω i = 1 ，此时的 W W 又会满足 WTW=1 W T W = 1 ，则有 WT=W−1 W T = W − 1 。

最后，特征分解的表达式可以写为：

A=WΣWT(7) (7) A = W Σ W T

注意到，这里的特征分解还有一个条件，那就是矩阵 A A 必须为方阵，如果不是方阵，即行列数不同时，这个公式就不成立。行列不同的情况就需要SVD登场了，这个留到下篇文章再讨论。

参考资料：
1、https://www.cnblogs.com/pinard/p/6251584.html

2、https://blog.csdn.net/u010182633/article/details/45921929