2020牛客暑期多校训练营(第一场) H题 Minimum-cost Flow【图论/最小费用最大流】

题目链接：https://ac.nowcoder.com/acm/contest/5666/H

题意

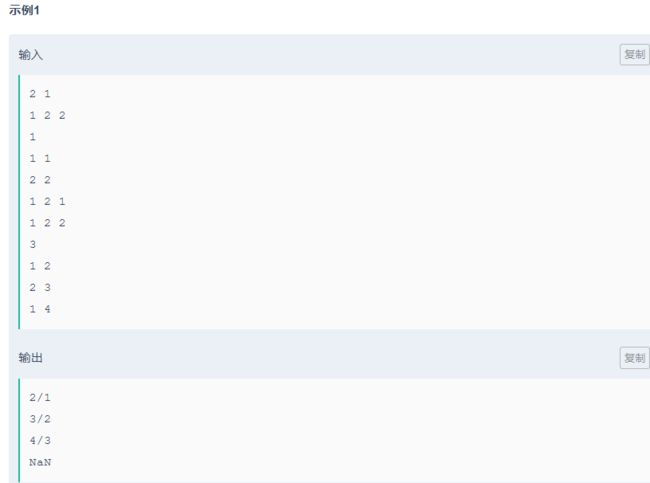
给你一个n个点，m条边的有向图，并给出每条边的费用。然后进行q次询问，每次询问给出每条边的容量（分数表示），并且所有边的容量相等。 对于每次询问，你需要输出总流量为1时，从点1到点n的最小费用（分数表示）。

思路

这题难的地方在于多次询问，q达到了1e5，那么如果对于每次询问都建图跑费用流肯定是会超时的。

那么不妨在询问前跑一次费用流，得到一些有用的信息，以便之后的每次查询能尽量做到O(1)的复杂度（实际上没有O(1)，因为分数化简需要求gcd，需要O(logn)复杂度）。

对于每次询问，总流量为1，每条边容量为u/v。考虑缩放，同时乘以v，则总流量为v，每条边容量为u，这时算出来的总费用除以v即为答案。 我们可以在询问之前，预处理得到所有增广路的费用，每次进行一次SPFA算法后，就能得到一条增广路的费用，将其记录于path数组中（按增广顺序能保证每条增广路费用是升序的），并求其前缀和，方便后续询问的处理。

查询之前，先预处理得到：
（1）path[a]，下标从0开始，表示单位容量(流量跑满，流量=容量)时第a+1条增广路费用。
（2）sum[a]，下标从1开始，表示单位容量(流量跑满，流量=容量)时前a条增广路总费用。

接下来处理每次询问。
假设v=a*u+b(b 由于sum和path是之前预处理得到的单位容量情况下的费用，所以sum[a]要乘以u得到流量为u时前a条增广路总费用，path[a]要乘以b得到流量为b时第a+1条增广路费用，则ans=(sum[a]*u+path[a]*b)/v。

AC代码

#pragma GCC optimize(2)
#include 
using namespace std;
typedef long long ll;
const ll N=1010,M=1010,inf=(1ll<<63)-1;
ll n,m,s,t,cnt,mincost,head[N],dis[N],vis[N],cur[N],sum[M];
vector<ll>path;
struct edge
{
    ll to,next,cap,cost;//cap是容量，cost是单位流量的花费
}e[M<<1];
void add(ll x,ll y,ll z,ll c)
{
    e[cnt].to=y;
    e[cnt].cap=z;
    e[cnt].cost=c;
    e[cnt].next=head[x];
    head[x]=cnt++;
}
void add_edge(ll x,ll y,ll z,ll c)
{
    add(x,y,z,c);
    add(y,x,0,-c);//反向边容量为0，单位流量的花费为-c
}
bool spfa()
{
    queue<int>q;
    for(ll i=1;i<=n;i++)
        dis[i]=inf;
    memset(vis,0,sizeof(vis));
    dis[s]=0;
    vis[s]=1;//入队标记
    q.push(s);
    while(!q.empty())
    {
        ll u=q.front();q.pop();
        vis[u]=0;//出队标记
        for(ll i=head[u];i!=-1;i=e[i].next)
        {
            ll v=e[i].to;
            if(e[i].cap>0&&dis[u]+e[i].cost<dis[v])
            {
                dis[v]=dis[u]+e[i].cost;
                if(!vis[v])
                {
                    vis[v]=1;//入队标记
                    q.push(v);
                }
            }
        }
    }//队列为空时 vis也全部被置为0
    if(dis[t]!=inf)return 1;
    return 0;
}
ll dfs(ll u,ll flow)
{
    vis[u]=1;//注意用vis标记走过的点，防止死循环
    if(u==t)return flow;//到达汇点，返回这条增广路上的最小流量
    for(ll& i=cur[u];i!=-1;i=e[i].next)
    {
        ll v=e[i].to;
        if(e[i].cap>0&&dis[v]==dis[u]+e[i].cost&&!vis[v])
        {
            ll di=dfs(v,min(flow,e[i].cap));//min(flow,e[i].w)表示起点到v的最小流量
            if(di>0)//防止dfs结果return 0的情况，如果di=0会死循环
            {
                e[i].cap-=di;
                e[i^1].cap+=di;//反向边加上di
                mincost+=di*e[i].cost;
                return di;//di表示整条增广路上的最小流量，回溯的时候一直向上返回，返回的di是不变的
            }
        }
    }
    vis[u]=0;//还原标记的点
    return 0;//找不到增广路，到不了汇点
}
ll dinic()
{
    ll maxflow=0;
    path.clear();
    while(spfa())//先spfa进行"探路"并分层，分层后进行多次dfs
    {
        path.push_back(dis[t]); // 每次spfa后得到一条增广路的费用
        memcpy(cur,head,sizeof(head));
        while(ll d=dfs(s,inf))//while循环的意义：只要dfs不为0，就一直dfs，直到找不到增广路
            maxflow+=d;
    }
    return maxflow;
}
// 以上都是dinic算法的模板，只是增加了path数组，用来在每次spfa后记录dis[t]。

int main()
{
    ios::sync_with_stdio(false);
    ll x,y,c,q,u,v;
    while(cin>>n>>m)
    {
        s=1,t=n;
        memset(head,-1,sizeof(head));
        cnt=0;
        mincost=0;
        for(ll i=1;i<=m;i++)
        {
            cin>>x>>y>>c;  // 点、边、费用
            add_edge(x,y,1,c); // 将每条边容量置为1
        }
        dinic(); // 跑费用流，得到path数组记录在单位容量的情况下，每条增广路上的费用(从小到大)
        ll pnum=path.size(); // 增广路个数
        for(ll i=0;i<pnum;i++)
            sum[i+1]=sum[i]+path[i]; // path[i]是第i+1条增广路费用
        // 查询之前，先预处理得到：
        // sum[a]，表示单位容量(流量跑满，流量=容量)时前a条增广路总费用
        // path[a]，表示单位容量(流量跑满，流量=容量)时第a+1条增广路费用
        cin>>q;
        while(q--)
        {
            cin>>u>>v;
            // 每条增广路容量由u/v扩成u，总流量由1扩成v，最后费用除以v即可
            if(u*pnum<v)printf("NaN\n"); // 容量<总流量
            else
            {
                // 假设：v=a*u+b(b
                ll a=v/u;
                ll b=v%u;
                // 由于sum和path是之前预处理得到的单位容量情况下的费用
                // 所以sum[a]要乘以u得到流量为u时前a条增广路总费用，
                // path[a]要乘以b得到流量为b时第a+1条增广路费用
                ll ans=sum[a]*u+path[a]*b;
                ll k=__gcd(ans,v);
                ans/=k;
                v/=k;
                printf("%lld/%lld\n",ans,v);
            }
        }
    }
    return 0;
}
/*
3 4
1 2 1
1 2 2
2 3 2
2 3 1
3
1 2
2 3
1 4

ans:
3/1
8/3
NaN
*/