视觉SLAM笔记(四)-对极几何
对极几何和PnP都是在已知若干对匹配点的情况下计算相机的运动,其中对极几何是计算2D-2D匹配点间的运动,而PnP是求解3D-2D匹配点对运动的方法
对极几何
对极约束
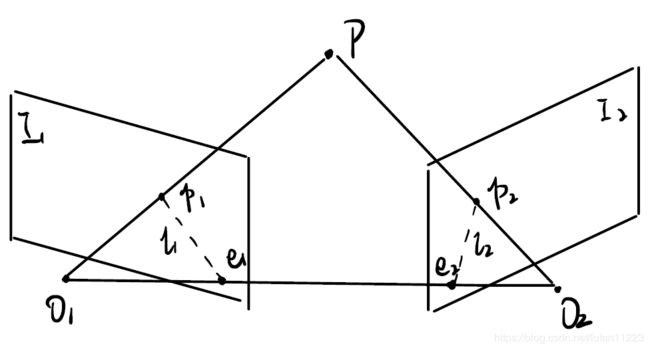
如图所示为对极几何约束,其中 I 1 , I 2 I_1,I_2 I1,I2为两帧图像, p 1 , p 2 p_1,p_2 p1,p2为两帧图像中所匹配的像素点, O 1 , O 2 O_1,O_2 O1,O2为相机的光心,连接 O 1 O 2 O_1O_2 O1O2交 I 1 , I 2 I_1,I_2 I1,I2于 e 1 , e 2 e_1,e_2 e1,e2点, e 1 , e 2 e_1,e_2 e1,e2称为极点,当 p 1 , p 2 p_1,p_2 p1,p2代表同一空间点在两幅图像中的投影时,理论上连接 O 1 p 1 O_1p_1 O1p1和 O 2 p 2 O_2p_2 O2p2,两条直线必交于空间中的一点 P P P, O 1 O 2 P O_1O_2P O1O2P所确定的平面成为极平面, O 1 O 2 O_1O_2 O1O2称为基线,极平面与像平面的交线 l 1 , l 2 l_1,l_2 l1,l2称为极线。
下面解释对极约束:
设 P = [ X , Y , Z ] P=[X,Y,Z] P=[X,Y,Z],以第一帧坐标系为起点,第二帧相对第一帧的旋转矩阵和平移向量分别为 R , t R,t R,t,根据相机模型,易知
Z p 1 = K P , Z p 2 = K ( R P + t ) Zp_1 = KP,Zp_2=K(RP+t) Zp1=KP,Zp2=K(RP+t)
当 p 1 , p 2 p_1,p_2 p1,p2为使用齐次坐标时,忽略上式中的 Z Z Z:
p 1 = K P , p 2 = K ( R P + t ) p_1 = KP,p_2=K(RP+t) p1=KP,p2=K(RP+t)
设 x 1 , x 2 x_1,x_2 x1,x2分别为 P P P在两个归一化平面上的投影(非像素坐标,与像素坐标相差一个相机内参矩阵)
p 1 = K x 1 , p 2 = K x 2 p_1 = Kx_1, p_2 = Kx_2 p1=Kx1,p2=Kx2
所以可得
x 2 = R x 1 + t x_2 = Rx_1+t x2=Rx1+t
两侧左乘 t ^ \hat{t} t^,得
t ^ x 2 = t ^ R x 1 \hat{t}x_2=\hat{t}Rx_1 t^x2=t^Rx1
两侧左乘 x 2 T x_2^T x2T,得
x 2 T t ^ x 2 = x 2 T t ^ R x 1 x_2^T\hat{t}x_2=x_2^T\hat{t}Rx_1 x2Tt^x2=x2Tt^Rx1
t ^ x 2 \hat{t}x_2 t^x2与 x 2 x_2 x2和 t t t均垂直,故 x 2 T t ^ x 2 = 0 x_2^T\hat{t}x_2=0 x2Tt^x2=0,得到如下约束
x 2 T t ^ R x 1 = 0 x_2^T\hat{t}Rx_1=0 x2Tt^Rx1=0
这个约束即为对极几何约束,将 p 1 , p 2 p_1,p_2 p1,p2带入可得
p 2 T K − T t ^ R K − 1 p 1 = 0 p_2^T K^{-T} \hat{t} R K^{-1} p_1=0 p2TK−Tt^RK−1p1=0
令 E = t ^ R E=\hat{t}R E=t^R,称为本质矩阵(Essential Matrix), F = K − T t ^ R K − 1 F= K^{-T} \hat{t} R K^{-1} F=K−Tt^RK−1为基础矩阵(Fundamental Matrix),对极约束如下:
x 2 T E x 1 = 0 , p 2 T F p 1 = 0 x_2^T E x_1=0, p_2^T F p_1=0 x2TEx1=0,p2TFp1=0
可见 E E E和 F F F间主要相差了相机内参 K K K,但通常认为相机内参已知(已标定),故通常使用 E E E
求解
E E E是一个 3 × 3 3\times3 3×3的矩阵,具有如下几个特性:
- 对 E E E进行SVD分解后, E = U Σ V T E=U\Sigma V^T E=UΣVT, Σ \Sigma Σ的形式为 Σ = d i a g { σ , σ , 0 } \Sigma=diag\lbrace \sigma,\sigma,0\rbrace Σ=diag{σ,σ,0}
- E E E具有尺度不变性,并且由于 R , t R,t R,t各有三个自由度,故 E E E共有5个自由度
求解 E E E有两种方式,一种是在本质矩阵所属的本质空间(Essential space)内求解 E E E,或者可以在对极几何约束下求解 E E E,再将其投影到本质空间中,通常情况下第二种方式较为简单,这里我们只考虑其尺度不变性,认为 E E E具有8个自由度,使用8对点来估计 E E E,即所谓的八点法
设 x 1 = [ u 1 , v 1 , 1 ] T x_1=[u_1,v_1,1]^T x1=[u1,v1,1]T, x 2 = [ u 2 , v 2 , 1 ] T x_2=[u_2,v_2,1]^T x2=[u2,v2,1]T
故
( u 1 , v 1 , 1 ) ( e 1 e 2 e 3 e 4 e 5 e 6 e 7 e 8 e 9 ) ( u 2 v 2 1 ) = 0 \left(u_{1}, v_{1}, 1\right)\left(\begin{array}{lll}{e_{1}} & {e_{2}} & {e_{3}} \\ {e_{4}} & {e_{5}} & {e_{6}} \\ {e_{7}} & {e_{8}} & {e_{9}}\end{array}\right)\left(\begin{array}{l}{u_{2}} \\ {v_{2}} \\ {1}\end{array}\right)=0 (u1,v1,1)⎝⎛e1e4e7e2e5e8e3e6e9⎠⎞⎝⎛u2v21⎠⎞=0
将 E E E写成向量的形式, e = [ e 1 , e 2 , e 3 , e 4 , e 5 , e 6 , e 7 , e 8 , e 9 ] T e=\left[e_{1}, e_{2}, e_{3}, e_{4}, e_{5}, e_{6}, e_{7}, e_{8}, e_{9}\right]^{T} e=[e1,e2,e3,e4,e5,e6,e7,e8,e9]T
对极约束可改写为如下形式:
[ u 1 u 2 , u 1 v 2 , u 1 , v 1 u 2 , v 1 v 2 , v 1 , u 2 , v 2 , 1 ] ⋅ e = 0 \left[u_{1} u_{2}, u_{1} v_{2}, u_{1}, v_{1} u_{2}, v_{1} v_{2}, v_{1}, u_{2}, v_{2}, 1\right] \cdot e=0 [u1u2,u1v2,u1,v1u2,v1v2,v1,u2,v2,1]⋅e=0
将8对点放到一个方程中,若8个方程线性不想关,则可按下面的方程解出 E E E的各元素
( u 1 1 u 2 1 u 1 1 v 2 1 u 1 1 v 1 1 u 2 1 v 1 1 v 2 1 v 1 1 u 2 1 v 2 1 1 u 1 2 u 2 2 u 1 2 v 2 2 u 1 2 v 1 2 u 2 2 v 1 2 v 2 2 v 1 2 u 2 2 v 2 2 1 ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ u 1 8 u 2 8 u 1 8 v 2 8 u 1 8 v 1 8 u 2 8 v 1 8 v 2 8 v 1 8 u 2 8 v 2 8 1 ) ( e 1 e 2 e 3 e 5 e 5 e 6 e 7 e 8 e 9 ) = 0 \left(\begin{array}{ccccccccc}{u_{1}^{1} u_{2}^{1}} & {u_{1}^{1} v_{2}^{1}} & {u_{1}^{1}} & {v_{1}^{1} u_{2}^{1}} & {v_{1}^{1} v_{2}^{1}} & {v_{1}^{1}} & {u_{2}^{1}} & {v_{2}^{1}} & {1} \\ {u_{1}^{2} u_{2}^{2}} & {u_{1}^{2} v_{2}^{2}} & {u_{1}^{2}} & {v_{1}^{2} u_{2}^{2}} & {v_{1}^{2} v_{2}^{2}} & {v_{1}^{2}} & {u_{2}^{2}} & {v_{2}^{2}} & {1} \\ {\vdots} & {\vdots} & {\vdots} & {\vdots} & {\vdots} & {\vdots} & {\vdots} & {\vdots} & {} \\ {u_{1}^{8} u_{2}^{8}} & {u_{1}^{8} v_{2}^{8}} & {u_{1}^{8}} & {v_{1}^{8} u_{2}^{8}} & {v_{1}^{8} v_{2}^{8}} & {v_{1}^{8}} & {u_{2}^{8}} & {v_{2}^{8}} & {1}\end{array}\right)\left(\begin{array}{l}{e_{1}} \\ {e_{2}} \\ {e_{3}} \\ {e_{5}} \\ {e_{5}} \\ {e_{6}} \\ {e_{7}} \\ {e_{8}} \\ {e_{9}}\end{array}\right)=0 ⎝⎜⎜⎜⎛u11u21u12u22⋮u18u28u11v21u12v22⋮u18v28u11u12⋮u18v11u21v12u22⋮v18u28v11v21v12v22⋮v18v28v11v12⋮v18u21u22⋮u28v21v22⋮v28111⎠⎟⎟⎟⎞⎝⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎛e1e2e3e5e5e6e7e8e9⎠⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎞=0
接下来可通过SVD分解求得 R , t R,t R,t
t 1 ∧ = U R Z ( π 2 ) Σ U T , R 1 = U R Z T ( π 2 ) V T t 1 ∧ = U R Z ( − π 2 ) Σ U T , R 1 = U R Z T ( − π 2 ) V T {t}_{1}^{\wedge}={U} {R}_{Z}\left(\frac{\pi}{2}\right) {\Sigma} {U}^{T},{R}_{1}={U} {R}_{Z}^{T}\left(\frac{\pi}{2}\right) {V}^{T}\\ {t}_{1}^{\wedge}={U} {R}_{Z}\left(-\frac{\pi}{2}\right) {\Sigma} {U}^{T},{R}_{1}={U} {R}_{Z}^{T}\left(-\frac{\pi}{2}\right) {V}^{T} t1∧=URZ(2π)ΣUT,R1=URZT(2π)VTt1∧=URZ(−2π)ΣUT,R1=URZT(−2π)VT
其中 R Z T ( π 2 ) {R}_{Z}^{T}\left(\frac{\pi}{2}\right) RZT(2π)表示一个旋转矩阵(沿 Z Z Z轴旋转90°的旋转矩阵),由于 E E E和 − E -E −E等价,对 t t t取负号结果不变,故共有四个解,但只有一种解 P P P在两个相机中都具有正的深度,带入检验即可
但是这种方式求得的 E E E,可能不满足 Σ = d i a g { σ , σ , 0 } \Sigma=diag\lbrace \sigma,\sigma,0\rbrace Σ=diag{σ,σ,0},将 E E E进行SVD分解后,得到 Σ = d i a g { σ 1 , σ 2 , σ 3 } \Sigma=diag\lbrace \sigma_1,\sigma_2,\sigma_3\rbrace Σ=diag{σ1,σ2,σ3},设 σ 1 ≥ σ 2 ≥ σ 3 \sigma_1\geq \sigma_2\geq \sigma_3 σ1≥σ2≥σ3,取
E = U d i a g ( σ 1 + σ 2 2 , σ 1 + σ 2 2 , 0 ) V T E=Udiag(\frac{\sigma_1+\sigma_2}{2},\frac{\sigma_1+\sigma_2}{2},0)V^T E=Udiag(2σ1+σ2,2σ1+σ2,0)VT
单应矩阵
单应矩阵(Homography)通常描述平面上的点在不同图像之间的变换关系,故也被称为planar homography,假设一对特征点 p 1 , p 2 p_1,p_2 p1,p2落在平面 P P P上,平面 P P P上的点满足方程
n T P + d = 0 ⇒ − n T P d = 1 n^TP+d=0 \Rightarrow -\frac{n^TP}{d}=1 nTP+d=0⇒−dnTP=1
根据相机投影模型:
p 2 = K ( R P + t ) = K ( R P − t n T P d ) = K ( R − t n T d ) P = K ( R − t n T d ) K − 1 p 1 p_2=K(RP+t)\\ =K(RP-t\frac{n^TP}{d})\\ =K(R-\frac{tn^T}{d})P\\ =K(R-\frac{tn^T}{d})K^{-1}p_1 p2=K(RP+t)=K(RP−tdnTP)=K(R−dtnT)P=K(R−dtnT)K−1p1
令 H = K ( R − t n T d ) K − 1 ∈ R 3 × 3 H=K(R-\frac{tn^T}{d})K^{-1} \in R^{3\times3} H=K(R−dtnT)K−1∈R3×3, H H H即为单应矩阵, p 2 = H p 1 p_2=Hp_1 p2=Hp1
首先根据匹配点对计算 H H H:
( u 2 v 2 1 ) = ( h 1 h 2 h 3 h 4 h 5 h 6 h 7 h 8 h 9 ) ( u 1 v 1 1 ) \left(\begin{array}{c}{u_{2}} \\ {v_{2}} \\ {1}\end{array}\right)=\left(\begin{array}{lll}{h_{1}} & {h_{2}} & {h_{3}} \\ {h_{4}} & {h_{5}} & {h_{6}} \\ {h_{7}} & {h_{8}} & {h_{9}}\end{array}\right)\left(\begin{array}{l}{u_{1}} \\ {v_{1}} \\ {1}\end{array}\right) ⎝⎛u2v21⎠⎞=⎝⎛h1h4h7h2h5h8h3h6h9⎠⎞⎝⎛u1v11⎠⎞
解得
u 2 = h 1 u 1 + h 2 v 1 + h 3 h 7 u 1 + h 8 v 1 + h 9 v 2 = h 4 u 1 + h 5 v 1 + h 6 h 7 u 1 + h 8 v 1 + h 9 u_{2}=\frac{h_{1} u_{1}+h_{2} v_{1}+h_{3}}{h_{7} u_{1}+h_{8} v_{1}+h_{9}} \\ v_{2}=\frac{h_{4} u_{1}+h_{5} v_{1}+h_{6}}{h_{7} u_{1}+h_{8} v_{1}+h_{9}} u2=h7u1+h8v1+h9h1u1+h2v1+h3v2=h7u1+h8v1+h9h4u1+h5v1+h6
整理得
h 1 u 1 + h 2 v 1 + h 3 − h 7 u 1 u 2 − h 8 v 1 u 2 = u 2 h 4 u 1 + h 5 v 1 + h 6 − h 7 u 1 v 2 − h 8 v 1 v 2 = v 2 h_{1} u_{1}+h_{2} v_{1}+h_{3}-h_{7} u_{1} u_{2}-h_{8} v_{1} u_{2}=u_{2}\\ h_{4} u_{1}+h_{5} v_{1}+h_{6}-h_{7} u_{1} v_{2}-h_{8} v_{1} v_{2}=v_{2} h1u1+h2v1+h3−h7u1u2−h8v1u2=u2h4u1+h5v1+h6−h7u1v2−h8v1v2=v2
故每个点对可提供两个方程得约束,共需要四个点对即可解出单应矩阵 H H H( H H H具有尺度等价性),在通过分解单应矩阵可以恢复出 R , t R,t R,t以及平面法向量
三角测量
三角测量得目的是在已知相机位姿的情况下根据对极几何估计出特征点在相机坐标系下的深度,根据对极几何,两相互匹配点的归一化坐标有如下关系:
s 2 x 2 = s 1 R x 1 + t s_2x_2=s_1Rx_1+t s2x2=s1Rx1+t
两边左乘 x 2 ^ \hat{x_2} x2^,得
x 2 ^ s 2 x 2 = s 1 x 2 ^ R x 2 + x 2 ^ t = 0 \hat{x_2}s_2x_2=s_1\hat{x_2}Rx_2 + \hat{x_2}t=0 x2^s2x2=s1x2^Rx2+x2^t=0
即得到了一个关于 s 1 s_1 s1的关系式,解出 s 1 s_1 s1,可继续解出 s 2 s_2 s2,至此完成深度恢复。
参考文献
[1] 高翔, 张涛, 颜沁睿, 刘毅, 视觉SLAM十四讲:从理论到实践, 电子工业出版社, 2017
[2] https://vision.in.tum.de/teaching/ss2019/mvg2019