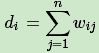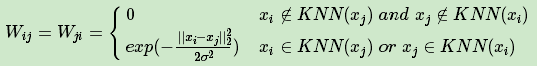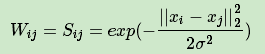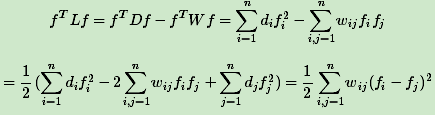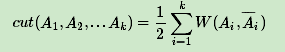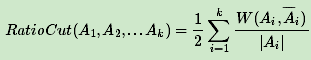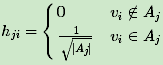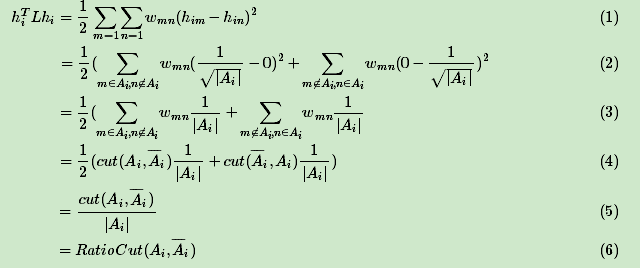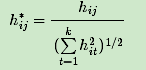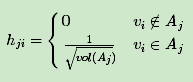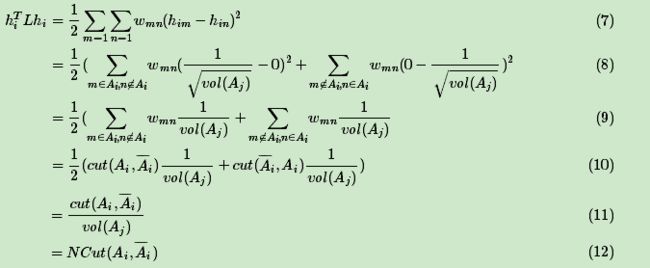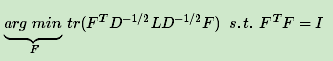聚类三种方法：k-means聚类、密度聚类、层次聚类和谱聚类Spectrum Clustering

简述

谱聚类是一种基于图论的聚类方法——将带权无向图划分为两个或两个以上的最优子图，使子图内部尽量相似，而子图间距离尽量距离较远，以达到常见的聚类的目的。其中的最优是指最优目标函数不同，可以是割边最小分割,也可以是分割规模差不多且割边最小的分割。

谱聚类算法首先根据给定的样本数据集定义一个描述成对数据点相似度的亲合矩阵,并且计算矩阵的特征值和特征向量，然后选择合适的特征向量聚类不同的数据点。谱聚类算法最初用于计算机视觉、VLS I 设计等领域，最近才开始用于机器学习中，并迅速成为国际上机器学习领域的研究热点。谱聚类算法建立在谱图理论基础上，其本质是将聚类问题转化为图的最优划分问题，是一种点对聚类算法，与传统的聚类算法相比，它具有能在任意形状的样本空间上聚类且收敛于全局最优解的优点。

根据不同的图拉普拉斯构造方法，可以得到不同的谱聚类算法形式。但是，这些算法的核心步骤都是相同的：

利用点对之间的相似性，构建亲和度矩阵；
构建拉普拉斯矩阵；
求解拉普拉斯矩阵最小的特征值对应的特征向量（通常舍弃零特征所对应的分量全相等的特征向量）；
由这些特征向量构成样本点的新特征，采用K-means等聚类方法完成最后的聚类。

谱聚类概述

谱聚类是从图论中演化过来的。主要思想是把所有的数据看做是空间中的点，这些点之间可以用边链接起来。距离比较远的两个点之间的边权重比较低，距离较近的两点之间权重较高，通过对所有的数据点组成的图进行切割，让切图后不同的子图间权重和尽可能低，而子图内的边权重和尽可能高，从而达到聚类的目的。

无向权重图

对于有边连接的两个点v_i和v_j,w_ij>0，若没有边连接，w_ij=0，度d_i定义为和它相连的所有边的权重之和，即

度矩阵D _nn 是一个对角矩阵，只有对角线有值，对应第i个点的度数：

邻近矩阵W_nn,第i行的第j个值对应我们的权重w _ij

相似矩阵

谱聚类中，通过样本点距离度量的相似矩阵S来获得邻接矩阵W。
构造邻接矩阵W的方法有ϵ -邻近法，K邻近法和全连接法。
ϵ -邻近法:设置距离阈值ϵ，然后用欧氏距离s_ij度量任意两点x_i和x_j的距离，即s_ij=||x_i-x_j||₂²
邻接矩阵W定义为：

由于不够准确，所以很少使用。
K邻近法
利用KNN算法遍历所有的样本点，取每个样本最近的k个点作为近邻，只有和样本距离最近的k个点之间的w _ij>0.为了保证对称性：

只要一个点在另一点的k近邻中，则保留S_ij
必须两个点互为k近邻，才保留S_ij

全连接法
相比前两种方法，第三种方法所有的点之间的权重值都大于0，因此称之为全连接法。可以选择不同的核函数来定义边权重，常用的有多项式核函数，高斯核函数和Sigmoid核函数。最常用的是高斯核函数RBF，此时相似矩阵和邻接矩阵相同：

在实际的应用中，使用第三种全连接法来建立邻接矩阵是最普遍的，而在全连接法中使用高斯径向核RBF是最普遍的。

拉普拉斯矩阵

L=D-W,D为度矩阵，是一个对角矩阵。W为邻接矩阵。
其性质如下：

拉普拉斯矩阵是对称矩阵，这可以由D和W都是对称矩阵而得。
由于拉普拉斯矩阵是对称矩阵，则它的所有的特征值都是实数。
对于任意的向量f，我们有
拉普拉斯矩阵是半正定的，且对应的n个实数特征值都大于等于0，即0=λ₁≤λ₂≤...≤λ_n，且最小的特征值为0。

无向图切图

对于无向图G的切图，我们的目标是将图G(V,E)切成相互没有连接的k个子图，每个子图点的集合为：A₁,A₂,..A_k，它们满足A_i∩A_j=∅,且A₁∪A₂∪...∪A_k=V

对于任意两个子图点的集合A,B⊂V, A∩B=∅, 我们定义A和B之间的切图权重为：

对于k个子图点的集合：A ₁,A ₂,..A _k,我们定义切图cut为：

中A¯ _i为Ai的补集。
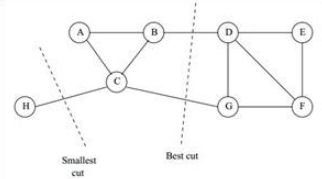
那么如何切图可以让子图内的点权重和高，子图间的点权重和低呢？一个自然的想法就是最小化cut(A ₁,A ₂,..A _k), 但是可以发现，这种极小化的切图存在问题，如下图：

我们选择一个权重最小的边缘的点，比如C和H之间进行cut，这样可以最小化cut(A ₁,A ₂,..A _k), 但是却不是最优的切图，如何避免这种切图，并且找到类似图中"Best Cut"这样的最优切图呢？

谱聚类之切图聚类

RatioCut切图

RatioCut切图为了避免最小切图，对每个切图，不光考虑最小化cut(A₁,A₂,..A_k)，它同时还考虑最大化每个子图点的个数，即：

接下来是最小化这个 RatioCut函数：
引入指示向量h _j={h ₁,h ₂,..h _k},j=1,2,..k,对于任意一个向量h _j,它是一个n维向量h _j,它是一个n维向量，定义h _ji为：

对于h _i ^TLh _i:

对应的RatioCut函数表达式为：

注意到H ^TH=I,则我们的切图优化目标为:

对于h _i ^TLh _i，我们的目标是找到最小的L的特征值,e而

则我们的目标就是找到k个最小的特征值，一般来说，k远远小于n，也就是说，此时我们进行了维度规约，将维度从n降到了k，从而近似可以解决这个NP难的问题。
通过找到L的最小的k个特征值，可以得到对应的k个特征向量，这k个特征向量组成一个nxk维度的矩阵，即为我们的H。一般需要对H矩阵按行做标准化，即

由于我们在使用维度规约的时候损失了少量信息，导致得到的优化后的指示向量h对应的H现在不能完全指示各样本的归属，因此一般在得到nxk维度的矩阵H后还需要对每一行进行一次传统的聚类，比如使用K-Means聚类.

Ncut切图

Ncut切图和RatioCut切图很类似，但是把Ratiocut的分母|Ai|换成vol(Ai). 由于子图样本的个数多并不一定权重就大，我们切图时基于权重也更合我们的目标，因此一般来说Ncut切图优于RatioCut切图。

对应的，Ncut切图对指示向量hh做了改进。注意到RatioCut切图的指示向量使用的是

标示样本归属，而Ncut切图使用了子图权重

来标示指示向量h，定义如下:

对于h _i ^TLh _i

优化目标函数为：

H ^TDH=I.推导如下：

最终为：

令H=D ^-1/2F,将指示向量矩阵H做一个小小的转化，使其为标准正交基，则H ^TLH=F ^TD ^-1/2LD ^-1/2F, H ^TDH=F ^TF=I
那么目标函数变为：

这样我们就可以继续按照RatioCut的思想，求出D^-1/2LD^-1/2的最小的前k个特征值，然后求出对应的特征向量，并标准化，得到最后的特征矩阵F,最后对F进行一次传统的聚类（比如K-Means）即可。
D^-1/2LD^-1/2相当于对拉普拉斯矩阵L做了一次标准化，

谱聚类算法流程

谱聚类主要的注意点为相似矩阵的生成方式，切图的方式以及最后的聚类方法。
最常用的相似矩阵的生成方式是基于高斯核距离的全连接方式，最常用的切图方式是Ncut。而到最后常用的聚类方法为K-Means。下面以Ncut总结谱聚类算法流程。

输入：样本集D=(x1,x2,...,xn)，相似矩阵的生成方式, 降维后的维度k1, 聚类方法，聚类后的维度k2
输出：簇划分C(c1,c2,...ck2)

根据输入的相似矩阵的生成方式构建样本的相似矩阵S
2）根据相似矩阵S构建邻接矩阵W，构建度矩阵D
3）计算出拉普拉斯矩阵L
4）构建标准化后的拉普拉斯矩阵D^-1/2LD^-1/2
5）计算D^-1/2LD^-1/2最小的k1个特征值所各自对应的特征向量f
将各自对应的特征向量f组成的矩阵按行标准化，最终组成n×k1维的特征矩阵F
7）对F中的每一行作为一个k1维的样本，共n个样本，用输入的聚类方法进行聚类，聚类维数为k2。
8）得到簇划分C(c1,c2,...ck2)

总结

谱聚类算法的主要优点有：
1）谱聚类只需要数据之间的相似度矩阵，因此对于处理稀疏数据的聚类很有效。这点传统聚类算法比如K-Means很难做到
2）由于使用了降维，因此在处理高维数据聚类时的复杂度比传统聚类算法好。
谱聚类算法的主要缺点有：
1）如果最终聚类的维度非常高，则由于降维的幅度不够，谱聚类的运行速度和最后的聚类效果均不好。

聚类效果依赖于相似矩阵，不同的相似矩阵得到的最终聚类效果可能很不同。

转自：https://www.cnblogs.com/pinard/p/6221564.html

谱聚类算法总结

简述