支持向量机(SVM)凸二次规划的求解——序列最小最优化算法(SMO)原理及python实现
原问题:
min α 1 2 ∑ i = 1 N ∑ j = 1 N α i α j y i y j K ( x i , x j ) − ∑ i = 1 N α i \min_\alpha\frac{1}{2}\sum_{i=1}^N\sum_{j=1}^N\alpha_i\alpha_jy_iy_jK(x_i,x_j)-\sum_{i=1}^N\alpha_i αmin21i=1∑Nj=1∑NαiαjyiyjK(xi,xj)−i=1∑Nαi
s.t.
∑ i = 1 N α i y i = 0 \sum_{i=1}^N\alpha_iy_i=0 i=1∑Nαiyi=0
0 ⩽ α i ⩽ C , i = 1 , 2 , ⋯ , N 0\leqslant\alpha_i\leqslant C, i=1,2,\cdots,N 0⩽αi⩽C,i=1,2,⋯,N
SMO算法的基本思想是:
如果所有变量的解都满足最优化问题的KKT条件,那么这个最优化问题的解就得到了。否则,选择两个变量,固定其他变量,针对这两个变量构建一个二次规划问题。
这样做的目的是,通过求解两个变量的二次规划问题,能不断靠近原有凸二次规划问题的解,并且计算方法有解析方法。
子问题有两个变量,其中一个为违反KKT条件最严重的那一个,另一个由约束条件自动确定。由与约束条件的存在,子问题实际上只有一个自由变量。
整个SMO算法包含两个部分:求解两个变量二次规划的解析方法和选择变量的启发式算法。
两个变量的二次规划求解方法
假设 α 1 , α 2 \alpha_1, \alpha_2 α1,α2为变量,其余的量为固定量
设问题的原始可行解为 α 1 o l d , α 2 o l d \alpha_1^{old}, \alpha_2^{old} α1old,α2old,最优解为 α 1 n e w , α 2 n e w \alpha_1^{new},\alpha_2^{new} α1new,α2new,并且在沿着约束方向未经剪辑时 α 2 \alpha_2 α2的最优解为 α 2 n e w , u n c \alpha_2^{new,unc} α2new,unc
由于约束条件存在,因此 α 2 n e w \alpha_2^{new} α2new的取值范围为:
L ⩽ α 2 n e w ⩽ H L\leqslant\alpha_2^{new}\leqslant H L⩽α2new⩽H
其中 L L L与 H H H是 α 2 n e w \alpha_2^{new} α2new所在的对角线段端点的界。
如果 y 1 ≠ y 2 y_1\not=y_2 y1=y2,则
L = max ( 0 , α 2 o l d − α 1 o l d ) , H = min ( C , C + α 2 o l d − α 1 o l d ) L=\max(0,\alpha_2^{old}-\alpha_1^{old}),\,\,\,\,\,H=\min(C,C+\alpha_2^{old}-\alpha_1^{old}) L=max(0,α2old−α1old),H=min(C,C+α2old−α1old)
如果 y 1 = y 2 y_1=y_2 y1=y2,则
L = max ( 0 , α 2 o l d + α 1 o l d − C ) , H = min ( C , α 2 o l d + α 1 o l d ) L=\max(0,\alpha_2^{old}+\alpha_1^{old}-C),\,\,\,\,\,H=\min(C,\alpha_2^{old}+\alpha_1^{old}) L=max(0,α2old+α1old−C),H=min(C,α2old+α1old)
下面先求未经剪辑的最优解 α 2 n e w , u n c \alpha_2^{new,unc} α2new,unc,记
g ( x ) = ∑ i = 1 N α i y i K ( x i , x ) + b g(x)=\sum_{i=1}^N\alpha_iy_iK(x_i,x)+b g(x)=i=1∑NαiyiK(xi,x)+b
令
E i = g ( x i ) − y i = ( ∑ j = 1 N α j y j K ( x j , x i ) + b ) , i = 1 , 2 E_i=g(x_i)-y_i=(\sum_{j=1}^N\alpha_jy_jK(x_j,x_i)+b), i=1,2 Ei=g(xi)−yi=(j=1∑NαjyjK(xj,xi)+b),i=1,2
当 i = 1 , 2 时 , E i 为 函 数 g ( x ) 对 输 入 x i 的 预 测 值 与 真 实 输 出 y i 之 差 。 当i=1,2时,E_i为函数g(x)对输入x_i的预测值与真实输出y_i之差。 当i=1,2时,Ei为函数g(x)对输入xi的预测值与真实输出yi之差。
定理:
最优化问题沿着约束方向未经剪辑的解时
α 2 n e w , u n c = α 2 o l d + y 2 ( E 1 − E 2 ) η \alpha_2^{new,unc}=\alpha_2^{old}+\frac{y_2(E_1-E_2)}{\eta} α2new,unc=α2old+ηy2(E1−E2)
其中,
η = K 11 + K 22 − K 12 = ∣ ∣ ϕ ( x 1 ) − ϕ ( x 2 ) ∣ ∣ 2 \eta=K_{11}+K_{22}-K_{12}=||\phi(x_1)-\phi(x_2)||^2 η=K11+K22−K12=∣∣ϕ(x1)−ϕ(x2)∣∣2
其中, ϕ ( x ) \phi(x) ϕ(x)是输入空间到特征空间的映射
经剪辑后 α 2 \alpha_2 α2的解, α 2 n e w = \alpha_2^{new}= α2new=
H , α 2 n e w , u n c > H H\,\,\,\,\,\,\,,\alpha_2^{new,unc}>H H,α2new,unc>H
α 2 n e w , u n c , L ⩽ α 2 n e w , u n c ⩽ H \alpha_2^{new,unc}\,\,\,\,\,\,\,,L\leqslant\alpha_2^{new,unc}\leqslant H α2new,unc,L⩽α2new,unc⩽H
L , α 2 n e w , u n c < L L\,\,\,\,\,\,\,,\alpha_2^{new,unc}
再由 α 2 n e w \alpha_2^{new} α2new求得 α 1 n e w \alpha_1^{new} α1new:
α 1 n e w = α 1 o l d + y 1 y 2 ( α 2 o l d − α 2 n e w ) \alpha_1^{new}=\alpha_1^{old}+y_1y_2(\alpha_2^{old}-\alpha_2^{new}) α1new=α1old+y1y2(α2old−α2new)
变量的选择方法
SMO算法在每个子问题中需要选择两个变量进行优化,并且至少一个变量是违反KKT条件的。
第一个变量的选择
外层循环,挑选在训练样本中选取违反KKT条件最严重的样本点,并将其对应的变量作为第一个变量。检验训练样本点 ( x i , x j ) (x_i,x_j) (xi,xj)是否满足KKT条件,即
α i = 0 ⇔ y i g ( x i ) ⩾ 1 \alpha_i=0\Leftrightarrow y_ig(x_i)\geqslant1 αi=0⇔yig(xi)⩾1
0 < α i < C ⇔ y i g ( x i ) = 1 0<\alpha_i
α i = C ⇔ y i g ( x i ) ⩽ 1 \alpha_i=C\Leftrightarrow y_ig(x_i)\leqslant1 αi=C⇔yig(xi)⩽1
其中, g ( x i ) = ∑ j = 1 N α j y j K ( x i , x j ) + b g(x_i)=\sum_{j=1}^N\alpha_jy_jK(x_i,x_j)+b g(xi)=∑j=1NαjyjK(xi,xj)+b
该检验是在 ϵ \epsilon ϵ范围内进行的。在检验过程中,外层循环首先遍历所有满足条件 0 < α i < C 0<\alpha_i
第二个变量选择
内层循环,假设已经寻找到了第一个变量 α 1 \alpha_1 α1,现在需要寻找 α 2 \alpha_2 α2,选择标准是希望能使 α 2 \alpha_2 α2有足够大的变化。
思路1:由于 α 2 n e w \alpha_2^{new} α2new是依赖于 ∣ E 1 − E 2 ∣ |E_1-E_2| ∣E1−E2∣的,,我们只需选择 α 2 \alpha_2 α2,使其对应的 ∣ E 1 − E 2 ∣ |E_1-E_2| ∣E1−E2∣最大。由于 E 1 E_1 E1已经确定,若 E 1 E_1 E1是正的,就选择最小的 E i E_i Ei作为 E 2 E_2 E2,如果 E 1 E_1 E1是负的,就选择最大的 E i E_i Ei作为 E 2 E_2 E2。
思路2:若思路1所选的 α 2 \alpha_2 α2不能使目标函数有足够的下降,则遍历所有在间隔边界上的支持向量点,依次作为 α 2 \alpha_2 α2试用,直到目标函数有足够的下降;若还是找不到,则遍历整个数据集;如何还是找不到,则抛弃 α 1 \alpha_1 α1,重新寻找新的 α 1 \alpha_1 α1。
计算阈值 b b b与差值 E i E_i Ei
每次完成两个变量的优化后,都需要重新计算阈值 b b b,当 0 < α 1 n e w < C 0<\alpha_1^{new}
∑ i = 1 N α i y i K i 1 + b = y 1 \sum_{i=1}^N\alpha_iy_iK_{i1}+b=y_1 i=1∑NαiyiKi1+b=y1
于是
b 1 n e w = y i − ∑ i = 3 N α i y i K i 1 − α 1 n e w y 1 K 11 − α 2 n e w y 2 K 21 b_1^{new}=y_i-\sum_{i=3}^N\alpha_iy_iK_{i1}-\alpha_1^{new}y_1K_{11}-\alpha_2^{new}y_2K_{21} b1new=yi−i=3∑NαiyiKi1−α1newy1K11−α2newy2K21
用 E 1 , E 2 E_1,E_2 E1,E2进行表示,有
b 1 n e w = − E 1 − y 1 K 11 ( α 1 n e w − α 1 o l d ) − y 2 K 21 ( α 2 n e w − α 2 o l d ) + b o l d b_1^{new}=-E_1-y_1K_{11}(\alpha_1^{new}-\alpha_1^{old})-y_2K_{21}(\alpha_2^{new}-\alpha_2^{old})+b^{old} b1new=−E1−y1K11(α1new−α1old)−y2K21(α2new−α2old)+bold
同理,如果 0 < α 2 n e w < C 0<\alpha_2^{new}
b 2 n e w = − E 2 − y 1 K 12 ( α 1 n e w − α 1 o l d ) − y 2 K 22 ( α 2 n e w − α 2 o l d ) + b o l d b_2^{new}=-E_2-y_1K_{12}(\alpha_1^{new}-\alpha_1^{old})-y_2K_{22}(\alpha_2^{new}-\alpha_2^{old})+b^{old} b2new=−E2−y1K12(α1new−α1old)−y2K22(α2new−α2old)+bold
如果 b 1 n e w , b 2 n e w b_1^{new},b_2^{new} b1new,b2new同时满足条件 0 < α i n e w < C , i = 1 , 2 0<\alpha_i^{new}
在每次完成两个变量的优化后,还必须更新对应的 E i E_i Ei值
E i n e w = ∑ S y j α i K ( x i , x j ) + b n e w − y i E_i^{new}=\sum_Sy_j\alpha_iK(x_i,x_j)+b^{new}-y_i Einew=S∑yjαiK(xi,xj)+bnew−yi
其中,S是所有支持向量 x j x_j xj的集合。
代码如下:
from sklearn import datasets
import matplotlib.pyplot as plt # 画图工具
import numpy as np
X, y = datasets.make_classification(n_samples=100, n_features=2, n_informative=2, n_redundant=0, n_repeated=0, n_classes=2, n_clusters_per_class=1, random_state=2)
for i in range(X.shape[0]):
if y[i] == 0:
y[i] = -1
#plt.scatter(X[:, 0], X[:, 1], c=y)
# plt.show()
class SMO:
def __init__(self, X, y, C, toler, maxIter): # samples labels constance tolerate maxIteration
self.X = X
self.y = y
self.C = C
self.toler = toler
self.maxIter = maxIter
self.N = self.X.shape[0]
self.b = 0
self.a = np.zeros(self.N)
self.K = np.zeros((self.N, self.N))
self.o = 0.5
for i in range(self.N):
for j in range(self.N):
t = 0
for k in range(self.X.shape[1]):
t += (self.X[i][k] - self.X[j][k])**2
self.K[i][j] = np.exp(-t/(2*self.o**2))
def select_J(self, i): # random choose j which is not equal to i.
j = i
while j == i:
j = np.random.randint(0, self.N)
return j
def fix_alpha(self, a, H, L):
if a > H:
a = H
if a < L:
a = L
return a
def cal_Ei(self, j):
t = 0
for i in range(self.N):
t += self.a[i]*self.y[i]*self.K[i][j]
return t + self.b - self.y[j]
def update(self):
iter = 0
while iter < self.maxIter:
alphaPairsChanged = 0
for i in range(self.N):
Ei = self.cal_Ei(i)
if (Ei < -self.toler and self.a[i] < self.C) or (Ei > self.toler and self.a[i] > 0):
j = self.select_J(i) # choose j != i
Ej = self.cal_Ei(j)
aiold = self.a[i]
ajold = self.a[j]
if self.y[i] != self.y[j]:
L = max(0, self.a[j] - self.a[i])
H = min(self.C, self.C + self.a[j] - self.a[i])
else:
L = max(0, self.a[j] + self.a[i] - self.C)
H = min(self.C, self.a[j] + self.a[i])
if L == H:
print("L==H")
continue
eta = self.K[i][i] + self.K[j][j] - 2*self.K[i][j]
if eta <= 0 :
print('eta <= 0')
continue
ajnew = ajold + self.y[j]*(Ei - Ej)/eta
ajnew = self.fix_alpha(ajnew, H, L)
if abs(ajnew - ajold) < 0.00001:
print("j not moving enough")
continue
self.a[j] = self.fix_alpha(ajnew, H, L)
self.a[i] = aiold + self.y[i]*self.y[j]*(ajold - ajnew)
b1 = -Ei - self.y[i]*self.K[i][i]*(self.a[i] - aiold) - self.y[j]*self.K[i][j]*(ajnew - ajold) + self.b
b2 = -Ej - self.y[i]*self.K[i][j]*(self.a[i] - aiold) - self.y[j]*self.K[j][j]*(ajnew - ajold) + self.b
if 0 < self.a[i] < self.C:
self.b = b1
elif 0 < self.a[j] < self.C:
self.b = b2
else:
self.b = (b1 + b2)/2
alphaPairsChanged += 1
if alphaPairsChanged == 0:
iter += 1
else:
iter = 0
return self.b, self.a
def score(self, X, y):
K = np.zeros((X.shape[0], self.N))
for i in range(X.shape[0]):
for j in range(self.N):
t = 0
for k in range(self.X.shape[1]):
t += (self.X[i][k] - self.X[j][k]) ** 2
K[i][j] = np.exp(-t / (2 * self.o ** 2))
y_pre = []
for i in range(X.shape[0]):
t = 0
for j in range(self.N):
t += self.a[j]*self.y[j]*K[i][j]
y_pre.append(t + self.b)
s = 0
for i in range(X.shape[0]):
if y_pre[i] < 0 and y[i] == -1:
s += 1
elif y_pre[i] > 0 and y[i] == 1:
s += 1
return s/X.shape[0]
L = SMO(X, y, 1, 0.001, 100)
b, a = L.update()
score = L.score(X, y)
print('b = {}'.format(b))
print('a = {}'.format(a))
print('the accuracy of this SVM is {}'.format(score))
运行代码,所得到的结果为:
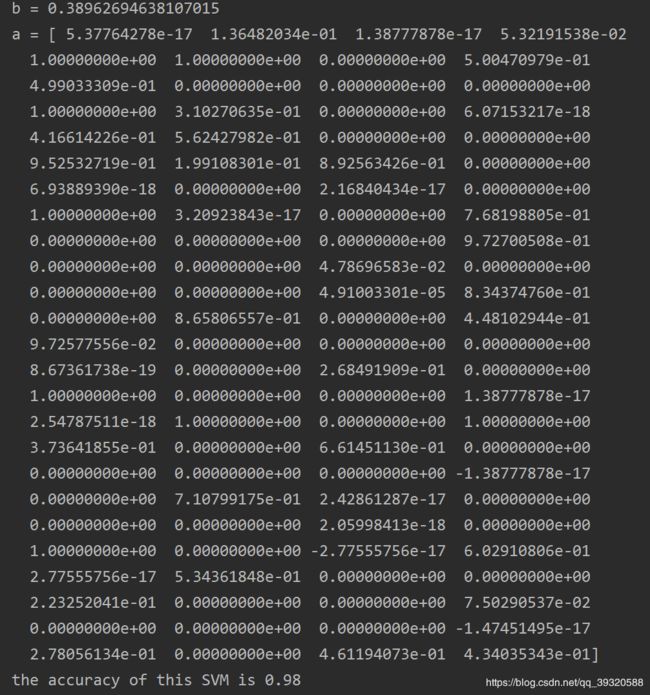
分别是对偶问题当中的变量 b , α b,\alpha b,α
以及最终训练出的SVM模型的精确度为98%